Question and Answers Forum

All Questions      Topic List

Arithmetic Questions

Previous in All Question      Next in All Question      

Previous in Arithmetic      Next in Arithmetic      

Question Number 113689 by Ar Brandon last updated on 14/Sep/20

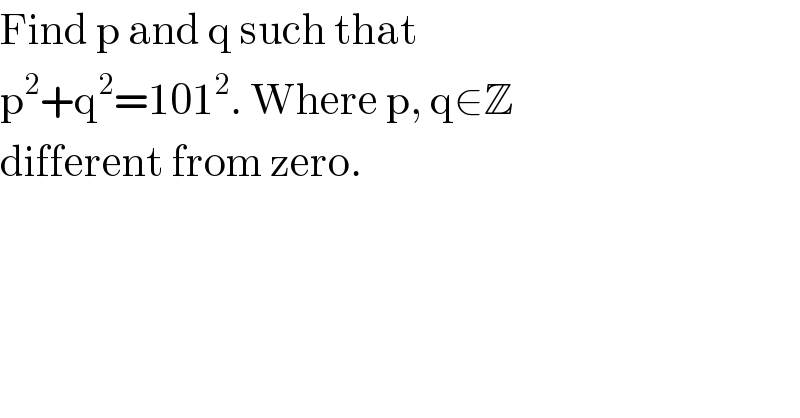
Find p and q such that p^2 +q^2 =101^2 . Where p, q∈Z different from zero.

$$\mathrm{Find}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{101}^{\mathrm{2}} .\:\mathrm{Where}\:\mathrm{p},\:\mathrm{q}\in\mathbb{Z}\: \\ $$$$\mathrm{different}\:\mathrm{from}\:\mathrm{zero}. \\ $$

Commented by Rasheed.Sindhi last updated on 14/Sep/20

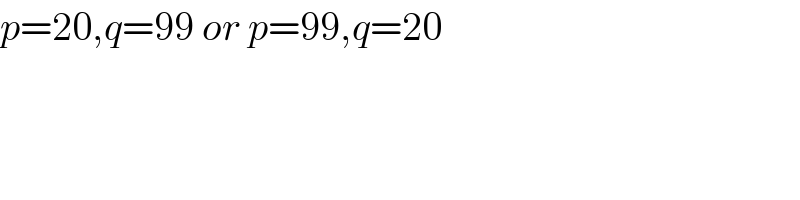
p=20,q=99 or p=99,q=20

$${p}=\mathrm{20},{q}=\mathrm{99}\:{or}\:{p}=\mathrm{99},{q}=\mathrm{20} \\ $$

Answered by nimnim last updated on 14/Sep/20

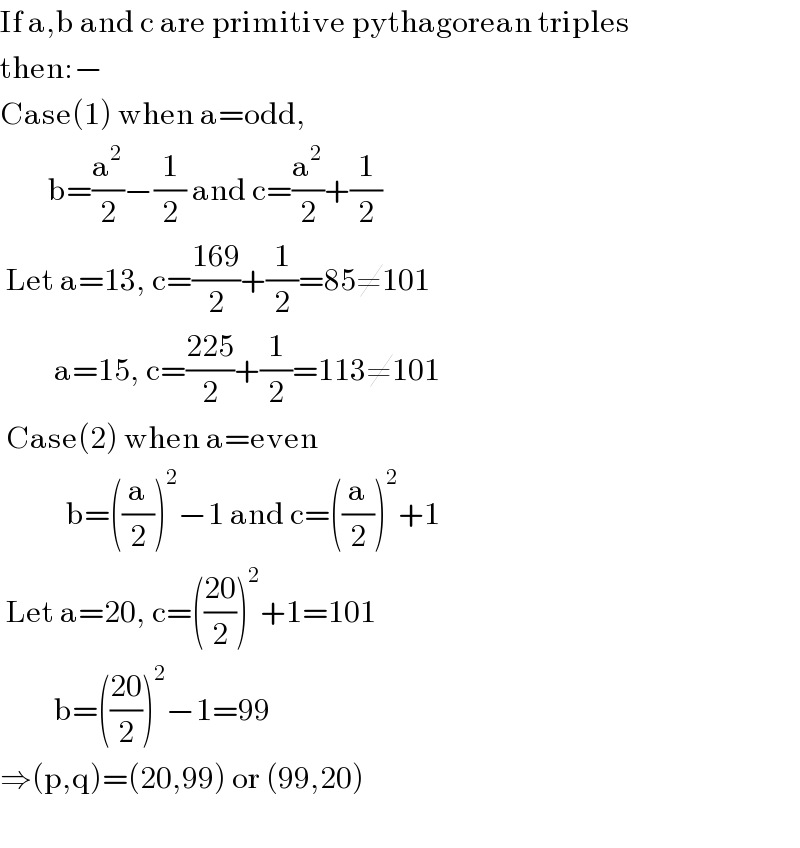
If a,b and c are primitive pythagorean triples then:− Case(1) when a=odd, b=(a^2 /2)−(1/2) and c=(a^2 /2)+(1/2) Let a=13, c=((169)/2)+(1/2)=85≠101 a=15, c=((225)/2)+(1/2)=113≠101 Case(2) when a=even b=((a/2))^2 −1 and c=((a/2))^2 +1 Let a=20, c=(((20)/2))^2 +1=101 b=(((20)/2))^2 −1=99 ⇒(p,q)=(20,99) or (99,20)

$$\mathrm{If}\:\mathrm{a},\mathrm{b}\:\mathrm{and}\:\mathrm{c}\:\mathrm{are}\:\mathrm{primitive}\:\mathrm{pythagorean}\:\mathrm{triples} \\ $$$$\mathrm{then}:− \\ $$$$\mathrm{Case}\left(\mathrm{1}\right)\:\mathrm{when}\:\mathrm{a}=\mathrm{odd}, \\ $$$$\:\:\:\:\:\:\:\:\mathrm{b}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}−\frac{\mathrm{1}}{\mathrm{2}}\:\mathrm{and}\:\mathrm{c}=\frac{\mathrm{a}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\:\mathrm{Let}\:\mathrm{a}=\mathrm{13},\:\mathrm{c}=\frac{\mathrm{169}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{85}\neq\mathrm{101} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{a}=\mathrm{15},\:\mathrm{c}=\frac{\mathrm{225}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}}=\mathrm{113}\neq\mathrm{101} \\ $$$$\:\mathrm{Case}\left(\mathrm{2}\right)\:\mathrm{when}\:\mathrm{a}=\mathrm{even} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\mathrm{b}=\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}\:\mathrm{and}\:\mathrm{c}=\left(\frac{\mathrm{a}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1} \\ $$$$\:\mathrm{Let}\:\mathrm{a}=\mathrm{20},\:\mathrm{c}=\left(\frac{\mathrm{20}}{\mathrm{2}}\right)^{\mathrm{2}} +\mathrm{1}=\mathrm{101} \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{b}=\left(\frac{\mathrm{20}}{\mathrm{2}}\right)^{\mathrm{2}} −\mathrm{1}=\mathrm{99} \\ $$$$\Rightarrow\left(\mathrm{p},\mathrm{q}\right)=\left(\mathrm{20},\mathrm{99}\right)\:\mathrm{or}\:\left(\mathrm{99},\mathrm{20}\right) \\ $$$$ \\ $$

Answered by Rasheed.Sindhi last updated on 15/Sep/20

If m & n are any positive integers with m>n (m^2 −n^2 ,2mn,m^2 +n^2 ) is a pathagorean triplet. This rule is perfect,it can produce all the pathagorean triplets and that also means that for every triplet there exist m & n which can produce that triplet. Here (p,q,101) is pathagorean triplet so m^2 +n^2 =101 or m^2 =101−n^2 . Clearly n≤⌊(√(101)) ⌋,so we′ve to find such n for which 101−n^2 is perfect square between 1 and 10. Hence n=1,10 are only proper values and corresponding values of m are 10 ,1.Since m>n so (m,n)=(10,1) p=m^2 −n^2 =10^2 −1^2 =99 q=2mn=2(10)(1)=20 Or p=2mn=20 q=m^2 −n^2 =99 Since p,q∈Z (p,q)=(20,99),(20,−99), (−20,99),(−20,−99), (99,20),(99,−20), (−99,20),(−99,−20).

$${If}\:{m}\:\&\:{n}\:\:{are}\:\:\boldsymbol{{any}}\:{positive} \\ $$$${integers}\:{with}\:{m}>{n} \\ $$$$\left({m}^{\mathrm{2}} −{n}^{\mathrm{2}} ,\mathrm{2}{mn},{m}^{\mathrm{2}} +{n}^{\mathrm{2}} \right)\:{is}\:{a} \\ $$$${pathagorean}\:{triplet}. \\ $$$$\mathcal{T}{his}\:{rule}\:{is}\:{perfect},{it}\:{can}\:{produce} \\ $$$$\boldsymbol{{all}}\:{the}\:{pathagorean}\:{triplets}\:{and} \\ $$$${that}\:{also}\:{means}\:{that}\:{for}\:\boldsymbol{{every}} \\ $$$${triplet}\:{there}\:{exist}\:{m}\:\&\:{n}\:{which} \\ $$$${can}\:{produce}\:{that}\:{triplet}. \\ $$$${Here}\:\left(\mathrm{p},\mathrm{q},\mathrm{101}\right)\:{is}\:{pathagorean} \\ $$$${triplet}\:{so}\:\:\:{m}^{\mathrm{2}} +{n}^{\mathrm{2}} =\mathrm{101} \\ $$$${or}\:{m}^{\mathrm{2}} =\mathrm{101}−{n}^{\mathrm{2}} .\:{Clearly} \\ $$$${n}\leqslant\lfloor\sqrt{\mathrm{101}}\:\rfloor,{so}\:{we}'{ve}\:{to}\:{find}\:{such} \\ $$$${n}\:{for}\:{which}\:\mathrm{101}−{n}^{\mathrm{2}} \:{is}\:{perfect} \\ $$$${square}\:{between}\:\mathrm{1}\:{and}\:\mathrm{10}. \\ $$$${Hence}\:{n}=\mathrm{1},\mathrm{10}\:{are}\:{only}\:{proper}\: \\ $$$${values}\:{and}\:{corresponding}\:{values} \\ $$$${of}\:{m}\:{are}\:\mathrm{10}\:,\mathrm{1}.{Since}\:{m}>{n}\:{so} \\ $$$$\left({m},{n}\right)=\left(\mathrm{10},\mathrm{1}\right) \\ $$$${p}={m}^{\mathrm{2}} −{n}^{\mathrm{2}} =\mathrm{10}^{\mathrm{2}} −\mathrm{1}^{\mathrm{2}} =\mathrm{99} \\ $$$${q}=\mathrm{2}{mn}=\mathrm{2}\left(\mathrm{10}\right)\left(\mathrm{1}\right)=\mathrm{20} \\ $$$${Or} \\ $$$${p}=\mathrm{2}{mn}=\mathrm{20} \\ $$$${q}={m}^{\mathrm{2}} −{n}^{\mathrm{2}} =\mathrm{99} \\ $$$${Since}\:{p},{q}\in\mathbb{Z} \\ $$$$\left({p},{q}\right)=\left(\mathrm{20},\mathrm{99}\right),\left(\mathrm{20},−\mathrm{99}\right), \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(−\mathrm{20},\mathrm{99}\right),\left(−\mathrm{20},−\mathrm{99}\right), \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\mathrm{99},\mathrm{20}\right),\left(\mathrm{99},−\mathrm{20}\right), \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\left(−\mathrm{99},\mathrm{20}\right),\left(−\mathrm{99},−\mathrm{20}\right). \\ $$

Answered by 1549442205PVT last updated on 16/Sep/20

We known that( a,b,c )is a triple of Pythagor posirive integer numbers where b^2 +c^2 =a^2 (a,b)=1if and only if c=uv,b=((u^2 −v^2 )/2), a=((u^2 +v^2 )/2) where u,v are odd and coprime .In the our problem p^2 +q^2 =101^2 (∗) Since 101 is a prime,so (p,q)=1. Hence,p=uv,q=((u^2 −v^2 )/2),((u^2 +v^2 )/2)=101 ⇔u^2 +v^2 =202⇒v<9<u≤13 i)If u=13 then v^2 =202−169=33⇒rejected ii)If u=11 then v^2 =202−121=81=9^2 ⇒v=9⇒p=uv=99,q=((11^2 −9^2 )/2)=20 Since p,q have equal role in the equation,we obtain (p,q)∈{(99,20),(20,99).From this follows (−p,q),(p,−q),(−p,−q) also satisfying second way: If(p,q)is a root of (∗) then (−p,q),(p,−q) and (−p,−q)are also roots of (∗).Hence we just need find pairs (p,q)of positive integer numbers of the equation(∗) Since 101 is a prime number,p and q are coprime( because suppose that gcd(p,q)=d≠1 then p=md,q=nd with (m,n)=1.Then p^2 +q^2 =101^2 (∗) ⇔(m^2 +n^2 )d^2 =101^2 ⇒101⋮d which is contradiction to the fact that 101 is prime) .Furthermore,among two numbers p,q must have one number is even and other number is odd.Hence,WLOG suppose p is odd and q is even.From that we have (∗)⇔p^2 =(101+q)(101−q) Put 101+q=m,101−q=n ⇒m>n,we get p^2 =mn,q=((m−n)/2),101=((m+n)/2). We see that m and n −coprime. because of suppose the contrary, that gcd(m,n)=d≠1.Then m=m_1 d,n=n_1 d From that 101=((m+n)/2)=((m_1 +n_1 )/2)d which is impossible since 101 is prime Therefore ,m and n are coprime.From p^2 =mn and (m,n)=1 we infer m=u^2 ,n=v^2 where u and v−coprime, u>v >0 and are odd numbers.Finally, we obtain { ((p=uv(1))),((q=((u^2 −v^2 )/2)(2))),((101=((u^2 +v^2 )/2)(3))) :} (3)⇔u^2 +v^2 =202⇒v<11≤u≤13 i)For u=13⇒v^2 =202−169=33⇒∄v∈Z ii)For u=11⇒v^2 =202−121=81 ⇒v=9.Put into (1)(2) we get (p,q)∈(99,20)and due to above note and the equality of p and q in equation we get (p,q)∈{99,20),(−99,20),(20,99),(20,−99), (99,−20),(−99,−20),(−20,99),(−20,−99)}

$$\mathrm{We}\:\mathrm{known}\:\mathrm{that}\left(\:\mathrm{a},\mathrm{b},\mathrm{c}\:\right)\mathrm{is}\:\mathrm{a}\:\mathrm{triple}\:\mathrm{of}\: \\ $$$$\mathrm{Pythagor}\:\mathrm{posirive}\:\mathrm{integer}\:\mathrm{numbers}\: \\ $$$$\mathrm{where}\:\mathrm{b}^{\mathrm{2}} +\mathrm{c}^{\mathrm{2}} =\mathrm{a}^{\mathrm{2}} \\ $$$$\left(\mathrm{a},\mathrm{b}\right)=\mathrm{1if}\:\mathrm{and}\:\mathrm{only}\:\mathrm{if}\:\mathrm{c}=\mathrm{uv},\mathrm{b}=\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{v}^{\mathrm{2}} }{\mathrm{2}}, \\ $$$$\mathrm{a}=\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} }{\mathrm{2}}\:\mathrm{where}\:\mathrm{u},\mathrm{v}\:\mathrm{are}\:\mathrm{odd}\:\mathrm{and}\:\mathrm{coprime} \\ $$$$.\mathrm{In}\:\mathrm{the}\:\mathrm{our}\:\mathrm{problem}\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{101}^{\mathrm{2}} \left(\ast\right) \\ $$$$\mathrm{Since}\:\mathrm{101}\:\mathrm{is}\:\mathrm{a}\:\mathrm{prime},\mathrm{so}\:\left(\mathrm{p},\mathrm{q}\right)=\mathrm{1}. \\ $$$$\mathrm{Hence},\mathrm{p}=\mathrm{uv},\mathrm{q}=\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{v}^{\mathrm{2}} }{\mathrm{2}},\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{101} \\ $$$$\Leftrightarrow\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} =\mathrm{202}\Rightarrow\mathrm{v}<\mathrm{9}<\mathrm{u}\leqslant\mathrm{13} \\ $$$$\left.\mathrm{i}\right)\mathrm{If}\:\mathrm{u}=\mathrm{13}\:\mathrm{then}\:\mathrm{v}^{\mathrm{2}} =\mathrm{202}−\mathrm{169}=\mathrm{33}\Rightarrow\mathrm{rejected} \\ $$$$\left.\mathrm{ii}\right)\mathrm{If}\:\mathrm{u}=\mathrm{11}\:\mathrm{then}\:\mathrm{v}^{\mathrm{2}} =\mathrm{202}−\mathrm{121}=\mathrm{81}=\mathrm{9}^{\mathrm{2}} \\ $$$$\Rightarrow\mathrm{v}=\mathrm{9}\Rightarrow\mathrm{p}=\mathrm{uv}=\mathrm{99},\mathrm{q}=\frac{\mathrm{11}^{\mathrm{2}} −\mathrm{9}^{\mathrm{2}} }{\mathrm{2}}=\mathrm{20} \\ $$$$\mathrm{Since}\:\mathrm{p},\mathrm{q}\:\:\mathrm{have}\:\:\mathrm{equal}\:\mathrm{role}\:\mathrm{in}\:\mathrm{the} \\ $$$$\mathrm{equation},\mathrm{we}\:\mathrm{obtain}\: \\ $$$$\left(\boldsymbol{\mathrm{p}},\boldsymbol{\mathrm{q}}\right)\in\left\{\left(\mathrm{99},\mathrm{20}\right),\left(\mathrm{20},\mathrm{99}\right).\mathrm{From}\:\mathrm{this}\right. \\ $$$$\mathrm{follows}\:\left(−\mathrm{p},\mathrm{q}\right),\left(\mathrm{p},−\mathrm{q}\right),\left(−\mathrm{p},−\mathrm{q}\right) \\ $$$$\mathrm{also}\:\mathrm{satisfying} \\ $$$$\boldsymbol{\mathrm{second}}\:\boldsymbol{\mathrm{way}}: \\ $$$$\mathrm{If}\left(\mathrm{p},\mathrm{q}\right)\mathrm{is}\:\mathrm{a}\:\mathrm{root}\:\mathrm{of}\:\left(\ast\right)\:\mathrm{then}\:\left(−\mathrm{p},\mathrm{q}\right),\left(\mathrm{p},−\mathrm{q}\right) \\ $$$$\mathrm{and}\:\left(−\mathrm{p},−\mathrm{q}\right)\mathrm{are}\:\mathrm{also}\:\mathrm{roots}\:\mathrm{of}\:\left(\ast\right).\mathrm{Hence} \\ $$$$\mathrm{we}\:\mathrm{just}\:\mathrm{need}\:\mathrm{find}\:\mathrm{pairs}\:\left(\mathrm{p},\mathrm{q}\right)\mathrm{of}\:\mathrm{positive} \\ $$$$\mathrm{integer}\:\mathrm{numbers}\:\mathrm{of}\:\mathrm{the}\:\mathrm{equation}\left(\ast\right) \\ $$$$\mathrm{Since}\:\mathrm{101}\:\mathrm{is}\:\mathrm{a}\:\mathrm{prime}\:\mathrm{number},\mathrm{p}\:\mathrm{and}\:\mathrm{q} \\ $$$$\mathrm{are}\:\mathrm{coprime}\left(\:\mathrm{because}\:\mathrm{suppose}\:\mathrm{that}\:\right. \\ $$$$\mathrm{gcd}\left(\mathrm{p},\mathrm{q}\right)=\mathrm{d}\neq\mathrm{1}\:\mathrm{then}\:\mathrm{p}=\mathrm{md},\mathrm{q}=\mathrm{nd}\:\mathrm{with} \\ $$$$\left(\mathrm{m},\mathrm{n}\right)=\mathrm{1}.\mathrm{Then}\:\mathrm{p}^{\mathrm{2}} +\mathrm{q}^{\mathrm{2}} =\mathrm{101}^{\mathrm{2}} \left(\ast\right) \\ $$$$\Leftrightarrow\left(\mathrm{m}^{\mathrm{2}} +\mathrm{n}^{\mathrm{2}} \right)\mathrm{d}^{\mathrm{2}} =\mathrm{101}^{\mathrm{2}} \Rightarrow\mathrm{101}\vdots\mathrm{d}\:\mathrm{which}\:\mathrm{is} \\ $$$$\left.\mathrm{contradiction}\:\mathrm{to}\:\mathrm{the}\:\mathrm{fact}\:\mathrm{that}\:\mathrm{101}\:\mathrm{is}\:\mathrm{prime}\right) \\ $$$$.\mathrm{Furthermore},\mathrm{among}\:\mathrm{two}\:\mathrm{numbers}\:\mathrm{p},\mathrm{q} \\ $$$$\mathrm{must}\:\mathrm{have}\:\mathrm{one}\:\mathrm{number}\:\mathrm{is}\:\mathrm{even}\:\mathrm{and}\:\mathrm{other} \\ $$$$\mathrm{number}\:\mathrm{is}\:\mathrm{odd}.\mathrm{Hence},\mathrm{WLOG}\:\mathrm{suppose} \\ $$$$\mathrm{p}\:\mathrm{is}\:\mathrm{odd}\:\mathrm{and}\:\mathrm{q}\:\mathrm{is}\:\mathrm{even}.\mathrm{From}\:\mathrm{that}\:\mathrm{we}\:\mathrm{have} \\ $$$$\:\left(\ast\right)\Leftrightarrow\mathrm{p}^{\mathrm{2}} =\left(\mathrm{101}+\mathrm{q}\right)\left(\mathrm{101}−\mathrm{q}\right) \\ $$$$\mathrm{Put}\:\mathrm{101}+\mathrm{q}=\mathrm{m},\mathrm{101}−\mathrm{q}=\mathrm{n}\:\Rightarrow\mathrm{m}>\mathrm{n},\mathrm{we} \\ $$$$\mathrm{get}\:\mathrm{p}^{\mathrm{2}} =\mathrm{mn},\mathrm{q}=\frac{\mathrm{m}−\mathrm{n}}{\mathrm{2}},\mathrm{101}=\frac{\mathrm{m}+\mathrm{n}}{\mathrm{2}}. \\ $$$$\mathrm{We}\:\mathrm{see}\:\mathrm{that}\:\mathrm{m}\:\mathrm{and}\:\mathrm{n}\:−\mathrm{coprime}. \\ $$$$\mathrm{because}\:\mathrm{of}\:\mathrm{suppose}\:\mathrm{the}\:\mathrm{contrary},\:\mathrm{that} \\ $$$$\mathrm{gcd}\left(\mathrm{m},\mathrm{n}\right)=\mathrm{d}\neq\mathrm{1}.\mathrm{Then}\:\mathrm{m}=\mathrm{m}_{\mathrm{1}} \mathrm{d},\mathrm{n}=\mathrm{n}_{\mathrm{1}} \mathrm{d} \\ $$$$\mathrm{From}\:\mathrm{that}\:\mathrm{101}=\frac{\mathrm{m}+\mathrm{n}}{\mathrm{2}}=\frac{\mathrm{m}_{\mathrm{1}} +\mathrm{n}_{\mathrm{1}} }{\mathrm{2}}\mathrm{d} \\ $$$$\mathrm{which}\:\:\mathrm{is}\:\mathrm{impossible}\:\mathrm{since}\:\mathrm{101}\:\mathrm{is}\:\mathrm{prime} \\ $$$$\mathrm{Therefore}\:,\mathrm{m}\:\mathrm{and}\:\mathrm{n}\:\mathrm{are}\:\mathrm{coprime}.\mathrm{From} \\ $$$$\mathrm{p}^{\mathrm{2}} =\mathrm{mn}\:\mathrm{and}\:\left(\mathrm{m},\mathrm{n}\right)=\mathrm{1}\:\mathrm{we}\:\mathrm{infer}\: \\ $$$$\mathrm{m}=\mathrm{u}^{\mathrm{2}} ,\mathrm{n}=\mathrm{v}^{\mathrm{2}} \mathrm{where}\:\mathrm{u}\:\mathrm{and}\:\mathrm{v}−\mathrm{coprime}, \\ $$$$\mathrm{u}>\mathrm{v}\:>\mathrm{0}\:\mathrm{and}\:\mathrm{are}\:\mathrm{odd}\:\mathrm{numbers}.\mathrm{Finally}, \\ $$$$\mathrm{we}\:\mathrm{obtain}\:\begin{cases}{\mathrm{p}=\mathrm{uv}\left(\mathrm{1}\right)}\\{\mathrm{q}=\frac{\mathrm{u}^{\mathrm{2}} −\mathrm{v}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{2}\right)}\\{\mathrm{101}=\frac{\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} }{\mathrm{2}}\left(\mathrm{3}\right)}\end{cases} \\ $$$$\left(\mathrm{3}\right)\Leftrightarrow\mathrm{u}^{\mathrm{2}} +\mathrm{v}^{\mathrm{2}} =\mathrm{202}\Rightarrow\mathrm{v}<\mathrm{11}\leqslant\mathrm{u}\leqslant\mathrm{13} \\ $$$$\left.\mathrm{i}\right)\mathrm{For}\:\mathrm{u}=\mathrm{13}\Rightarrow\mathrm{v}^{\mathrm{2}} =\mathrm{202}−\mathrm{169}=\mathrm{33}\Rightarrow\nexists\mathrm{v}\in\mathbb{Z} \\ $$$$\left.\mathrm{ii}\right)\mathrm{For}\:\mathrm{u}=\mathrm{11}\Rightarrow\mathrm{v}^{\mathrm{2}} =\mathrm{202}−\mathrm{121}=\mathrm{81} \\ $$$$\Rightarrow\mathrm{v}=\mathrm{9}.\mathrm{Put}\:\mathrm{into}\:\left(\mathrm{1}\right)\left(\mathrm{2}\right)\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{p},\mathrm{q}\right)\in\left(\mathrm{99},\mathrm{20}\right)\mathrm{and}\:\mathrm{due}\:\mathrm{to}\:\mathrm{above}\:\mathrm{note}\:\mathrm{and}\:\mathrm{the} \\ $$$$\mathrm{equality}\:\mathrm{of}\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\:\mathrm{in}\:\mathrm{equation}\:\mathrm{we}\:\mathrm{get} \\ $$$$\left(\mathrm{p},\mathrm{q}\right)\in\left\{\mathrm{99},\mathrm{20}\right),\left(−\mathrm{99},\mathrm{20}\right),\left(\mathrm{20},\mathrm{99}\right),\left(\mathrm{20},−\mathrm{99}\right), \\ $$$$\left.\left(\mathrm{99},−\mathrm{20}\right),\left(−\mathrm{99},−\mathrm{20}\right),\left(−\mathrm{20},\mathrm{99}\right),\left(−\mathrm{20},−\mathrm{99}\right)\right\} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com