Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 62244 by Rasheed.Sindhi last updated on 18/Jun/19

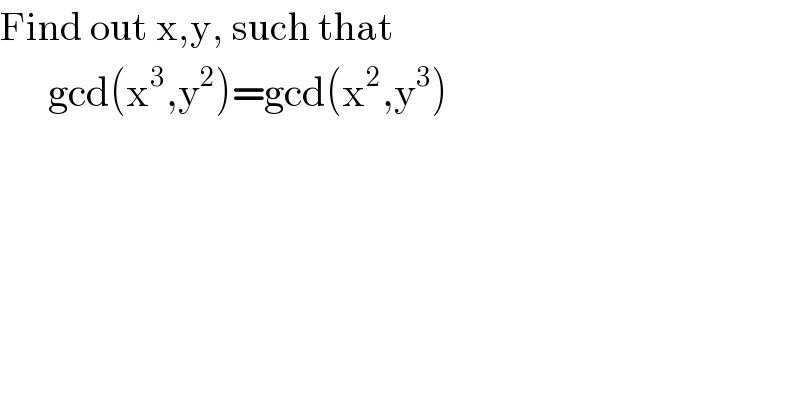
Find out x,y, such that gcd(x^3 ,y^2 )=gcd(x^2 ,y^3 )

$$\mathrm{Find}\:\mathrm{out}\:\mathrm{x},\mathrm{y},\:\mathrm{such}\:\mathrm{that} \\ $$$$\:\:\:\:\:\:\mathrm{gcd}\left(\mathrm{x}^{\mathrm{3}} ,\mathrm{y}^{\mathrm{2}} \right)=\mathrm{gcd}\left(\mathrm{x}^{\mathrm{2}} ,\mathrm{y}^{\mathrm{3}} \right) \\ $$

Commented by mr W last updated on 18/Jun/19

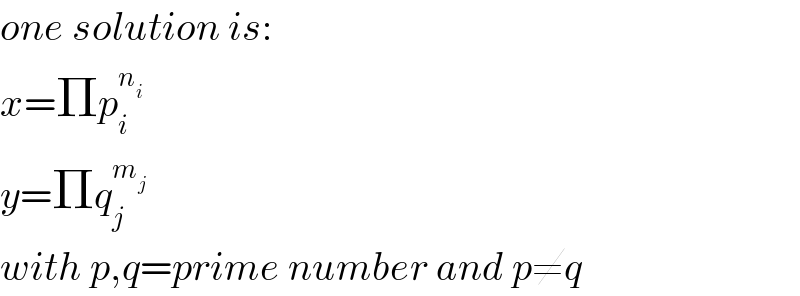
one solution is: x=Πp_i ^n_i y=Πq_j ^m_j with p,q=prime number and p≠q

$${one}\:{solution}\:{is}: \\ $$$${x}=\Pi{p}_{{i}} ^{{n}_{{i}} } \\ $$$${y}=\Pi{q}_{{j}} ^{{m}_{{j}} } \\ $$$${with}\:{p},{q}={prime}\:{number}\:{and}\:{p}\neq{q} \\ $$

Commented by Rasheed.Sindhi last updated on 19/Jun/19

Thanks Sir! Waiting for solutions when x & y are noncoprime with some workings.

$$\mathcal{T}{hanks}\:\mathcal{S}{ir}!\: \\ $$$${Waiting}\:{for}\:{solutions}\:\mathrm{w}{hen}\:{x}\:\&\:{y}\:{are} \\ $$$$\:\:{noncoprime}\:{with}\:{some}\:{workings}. \\ $$

Commented by Rasheed.Sindhi last updated on 23/Jun/19

The question having no market value!

$$\mathcal{T}{he}\:{question}\:{having}\:{no}\:{market}\:{value}! \\ $$

Answered by Rasheed.Sindhi last updated on 21/Jun/19

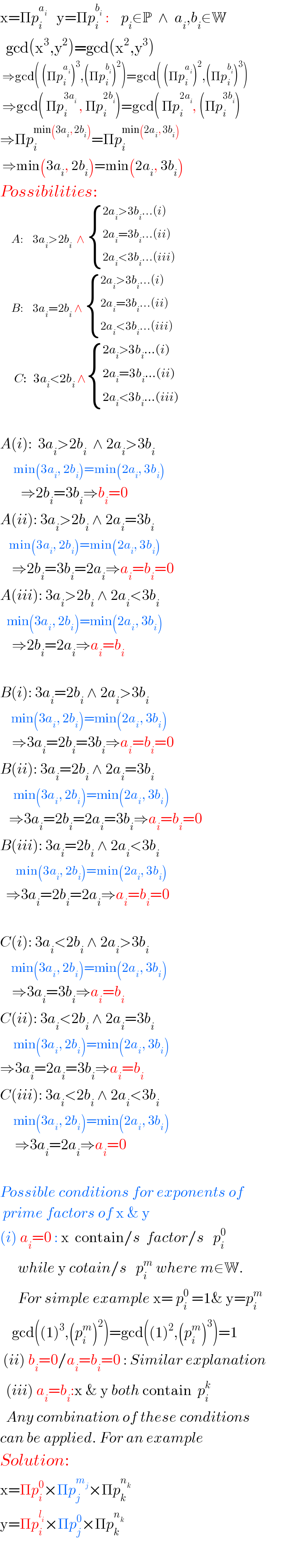
x=Πp_i ^a_i y=Πp_i ^b_i : p_i ∈P ∧ a_i ,b_i ∈W gcd(x^3 ,y^2 )=gcd(x^2 ,y^3 ) ⇒gcd( (Πp_i ^a_i )^3 ,(Πp_i ^b_i )^2 )=gcd( (Πp_i ^a_i )^2 ,(Πp_i ^b_i )^3 ) ⇒gcd( Πp_i ^(3a_i ) , Πp_i ^(2b_i ) )=gcd( Πp_i ^(2a_i ) , (Πp_i ^(3b_i ) ) ⇒Πp_i ^(min(3a_i , 2b_i )) =Πp_i ^(min(2a_i , 3b_i )) ⇒min(3a_i , 2b_i )=min(2a_i , 3b_i ) Possibilities: A: 3a_i >2b_i ∧ { ((2a_i >3b_i ...(i))),((2a_i =3b_i ...(ii))),((2a_i <3b_i ...(iii))) :} B: 3a_i =2b_i ∧ { ((2a_i >3b_i ...(i))),((2a_i =3b_i ...(ii))),((2a_i <3b_i ...(iii))) :} _ C: 3a_i <2b_i ∧ { ((2a_i >3b_i ...(i))),((2a_i =3b_i ...(ii))),((2a_i <3b_i ...(iii))) :} A(i): 3a_i >2b_i ∧ 2a_i >3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒2b_i =3b_i ⇒b_i =0 A(ii): 3a_i >2b_i ∧ 2a_i =3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒2b_i =3b_i =2a_i ⇒a_i =b_i =0 A(iii): 3a_i >2b_i ∧ 2a_i <3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒2b_i =2a_i ⇒a_i =b_i B(i): 3a_i =2b_i ∧ 2a_i >3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒3a_i =2b_i =3b_i ⇒a_i =b_i =0 B(ii): 3a_i =2b_i ∧ 2a_i =3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒3a_i =2b_i =2a_i =3b_i ⇒a_i =b_i =0 B(iii): 3a_i =2b_i ∧ 2a_i <3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒3a_i =2b_i =2a_i ⇒a_i =b_i =0 C(i): 3a_i <2b_i ∧ 2a_i >3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒3a_i =3b_i ⇒a_i =b_i C(ii): 3a_i <2b_i ∧ 2a_i =3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒3a_i =2a_i =3b_i ⇒a_i =b_i C(iii): 3a_i <2b_i ∧ 2a_i <3b_i min(3a_i , 2b_i )=min(2a_i , 3b_i ) ⇒3a_i =2a_i ⇒a_i =0 Possible conditions for exponents of prime factors of x & y (i) a_i =0 : x contain/s factor/s p_i ^0 while y cotain/s p_i ^m where m∈W. For simple example x= p_i ^0 =1& y=p_i ^m gcd((1)^3 ,(p_i ^m )^2 )=gcd((1)^2 ,(p_i ^m )^3 )=1 (ii) b_i =0/a_i =b_i =0 : Similar explanation (iii) a_i =b_i :x & y both contain p_i ^k Any combination of these conditions can be applied. For an example Solution: x=Πp_i ^0 ×Πp_j ^m_j ×Πp_k ^n_k y=Πp_i ^l_i ×Πp_j ^0 ×Πp_k ^n_k

$$\mathrm{x}=\Pi{p}_{{i}} ^{{a}_{{i}} } \:\:\:\mathrm{y}=\Pi{p}_{{i}} ^{{b}_{{i}} } \::\:\:\:\:{p}_{{i}} \in\mathbb{P}\:\:\wedge\:\:{a}_{{i}} ,{b}_{{i}} \in\mathbb{W} \\ $$$$\:\:\mathrm{gcd}\left(\mathrm{x}^{\mathrm{3}} ,\mathrm{y}^{\mathrm{2}} \right)=\mathrm{gcd}\left(\mathrm{x}^{\mathrm{2}} ,\mathrm{y}^{\mathrm{3}} \right) \\ $$$$\:\Rightarrow\mathrm{gcd}\left(\:\left(\Pi{p}_{{i}} ^{{a}_{{i}} } \right)^{\mathrm{3}} ,\left(\Pi{p}_{{i}} ^{{b}_{{i}} } \right)^{\mathrm{2}} \right)=\mathrm{gcd}\left(\:\left(\Pi{p}_{{i}} ^{{a}_{{i}} } \right)^{\mathrm{2}} ,\left(\Pi{p}_{{i}} ^{{b}_{{i}} } \right)^{\mathrm{3}} \right) \\ $$$$\:\Rightarrow\mathrm{gcd}\left(\:\Pi{p}_{{i}} ^{\mathrm{3}{a}_{{i}} } \:,\:\Pi{p}_{{i}} ^{\mathrm{2}{b}_{{i}} } \right)=\mathrm{gcd}\left(\:\Pi{p}_{{i}} ^{\mathrm{2}{a}_{{i}} } ,\:\left(\Pi{p}_{{i}} ^{\mathrm{3}{b}_{{i}} } \right)\right. \\ $$$$\Rightarrow\Pi{p}_{{i}} ^{\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)} =\Pi{p}_{{i}} ^{\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right)} \\ $$$$\:\Rightarrow\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$${Possibilities}: \\ $$$$\:\:\:\:\:{A}:\:\:\:\:\mathrm{3}{a}_{{i}} >\mathrm{2}{b}_{{i}} \:\:\wedge\:\begin{cases}{\mathrm{2}{a}_{{i}} >\mathrm{3}{b}_{{i}} ...\left({i}\right)}\\{\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} ...\left({ii}\right)}\\{\mathrm{2}{a}_{{i}} <\mathrm{3}{b}_{{i}} ...\left({iii}\right)}\end{cases} \\ $$$$\:\:\:\:\:{B}:\:\:\:\:\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} \:\wedge\:\begin{cases}{\mathrm{2}{a}_{{i}} >\mathrm{3}{b}_{{i}} ...\left({i}\right)}\\{\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} ...\left({ii}\right)}\\{\mathrm{2}{a}_{{i}} <\mathrm{3}{b}_{{i}} ...\left({iii}\right)}\end{cases} \\ $$$$\:_{} \:\:\:\:{C}:\:\:\:\mathrm{3}{a}_{{i}} <\mathrm{2}{b}_{{i}} \:\wedge\begin{cases}{\mathrm{2}{a}_{{i}} >\mathrm{3}{b}_{{i}} ...\left({i}\right)}\\{\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} ...\left({ii}\right)}\\{\mathrm{2}{a}_{{i}} <\mathrm{3}{b}_{{i}} ...\left({iii}\right)}\end{cases} \\ $$$$ \\ $$$${A}\left({i}\right):\:\:\mathrm{3}{a}_{{i}} >\mathrm{2}{b}_{{i}} \:\:\wedge\:\mathrm{2}{a}_{{i}} >\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\:\:\:\:\Rightarrow\mathrm{2}{b}_{{i}} =\mathrm{3}{b}_{{i}} \Rightarrow{b}_{{i}} =\mathrm{0} \\ $$$${A}\left({ii}\right):\:\mathrm{3}{a}_{{i}} >\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\:\Rightarrow\mathrm{2}{b}_{{i}} =\mathrm{3}{b}_{{i}} =\mathrm{2}{a}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} =\mathrm{0} \\ $$$${A}\left({iii}\right):\:\mathrm{3}{a}_{{i}} >\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} <\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\:\Rightarrow\mathrm{2}{b}_{{i}} =\mathrm{2}{a}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} \\ $$$$ \\ $$$${B}\left({i}\right):\:\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} >\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\:\Rightarrow\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} =\mathrm{3}{b}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} =\mathrm{0} \\ $$$${B}\left({ii}\right):\:\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\Rightarrow\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} =\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} =\mathrm{0} \\ $$$${B}\left({iii}\right):\:\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} <\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\Rightarrow\mathrm{3}{a}_{{i}} =\mathrm{2}{b}_{{i}} =\mathrm{2}{a}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} =\mathrm{0} \\ $$$$ \\ $$$${C}\left({i}\right):\:\mathrm{3}{a}_{{i}} <\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} >\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\:\Rightarrow\mathrm{3}{a}_{{i}} =\mathrm{3}{b}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} \\ $$$${C}\left({ii}\right):\:\mathrm{3}{a}_{{i}} <\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\Rightarrow\mathrm{3}{a}_{{i}} =\mathrm{2}{a}_{{i}} =\mathrm{3}{b}_{{i}} \Rightarrow{a}_{{i}} ={b}_{{i}} \\ $$$${C}\left({iii}\right):\:\mathrm{3}{a}_{{i}} <\mathrm{2}{b}_{{i}} \:\wedge\:\mathrm{2}{a}_{{i}} <\mathrm{3}{b}_{{i}} \\ $$$$\:\:\:\:\:\:\mathrm{min}\left(\mathrm{3}{a}_{{i}} ,\:\mathrm{2}{b}_{{i}} \right)=\mathrm{min}\left(\mathrm{2}{a}_{{i}} ,\:\mathrm{3}{b}_{{i}} \right) \\ $$$$\:\:\:\:\:\Rightarrow\mathrm{3}{a}_{{i}} =\mathrm{2}{a}_{{i}} \Rightarrow{a}_{{i}} =\mathrm{0} \\ $$$$ \\ $$$${Possible}\:{conditions}\:{for}\:{exponents}\:{of} \\ $$$$\:{prime}\:{factors}\:{of}\:\mathrm{x}\:\&\:\mathrm{y} \\ $$$$\left({i}\right)\:{a}_{{i}} =\mathrm{0}\::\:\mathrm{x}\:\:\mathrm{contain}/{s}\:\:{factor}/{s}\:\:\:{p}_{{i}} ^{\mathrm{0}} \\ $$$$\:\:\:\:\:\:{while}\:\mathrm{y}\:{cotain}/{s}\:\:\:{p}_{{i}} ^{{m}} \:{where}\:{m}\in\mathbb{W}. \\ $$$$\:\:\:\:\:\:{For}\:{simple}\:{example}\:\mathrm{x}=\:{p}_{{i}} ^{\mathrm{0}} \:=\mathrm{1\&}\:\mathrm{y}={p}_{{i}} ^{{m}} \\ $$$$\:\:\:\:\mathrm{gcd}\left(\left(\mathrm{1}\right)^{\mathrm{3}} ,\left({p}_{{i}} ^{{m}} \right)^{\mathrm{2}} \right)=\mathrm{gcd}\left(\left(\mathrm{1}\right)^{\mathrm{2}} ,\left({p}_{{i}} ^{{m}} \right)^{\mathrm{3}} \right)=\mathrm{1} \\ $$$$\:\left({ii}\right)\:{b}_{{i}} =\mathrm{0}/{a}_{{i}} ={b}_{{i}} =\mathrm{0}\::\:{Similar}\:{explanation} \\ $$$$\:\:\left({iii}\right)\:{a}_{{i}} ={b}_{{i}} :\mathrm{x}\:\&\:\mathrm{y}\:{both}\:\mathrm{contain}\:\:{p}_{{i}} ^{{k}} \\ $$$$\:\:{Any}\:{combination}\:{of}\:{these}\:{conditions} \\ $$$${can}\:{be}\:{applied}.\:{For}\:{an}\:{example} \\ $$$${Solution}: \\ $$$$\mathrm{x}=\Pi{p}_{{i}} ^{\mathrm{0}} ×\Pi{p}_{{j}} ^{{m}_{{j}} } ×\Pi{p}_{{k}} ^{{n}_{{k}} } \\ $$$$\mathrm{y}=\Pi{p}_{{i}} ^{{l}_{{i}} } ×\Pi{p}_{{j}} ^{\mathrm{0}} ×\Pi{p}_{{k}} ^{{n}_{{k}} } \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 21/Jun/19

Note:The answer is almost complete although it is not perfect. The answer suggest a general method how to compose x & y to meet the condition gcd(x^3 ,y^2 )=gcd(x^2 ,y^3 ) Rule1: If any prime factor in x (or y) has exponent 0, same prime in y(or in x) has any exponent from whole numbers. Rule2: If any prime has exponent other than 0 in x (or y),same prime in y(or x has same exponent. x=3^2 .7^0 .2^4 =144 y=3^2 .7^3 .2^0 =3087 ^• exponents equal ^• exponent 0 in a primefactor of x Any exponent in the same prime of y ^• exponent 0 in a primefactor of y Any exponent in the same prime of x

$${Note}:{The}\:{answer}\:{is}\:{almost}\:{complete} \\ $$$${although}\:{it}\:{is}\:{not}\:{perfect}. \\ $$$${The}\:{answer}\:{suggest}\:{a}\:\mathrm{general}\:{method}\:{how}\:{to} \\ $$$${compose}\:\mathrm{x}\:\&\:\mathrm{y}\:{to}\:{meet}\:{the}\:{condition} \\ $$$$\:\:\:\mathrm{gcd}\left(\mathrm{x}^{\mathrm{3}} ,\mathrm{y}^{\mathrm{2}} \right)=\mathrm{gcd}\left(\mathrm{x}^{\mathrm{2}} ,\mathrm{y}^{\mathrm{3}} \right) \\ $$$$ \\ $$$${Rule}\mathrm{1}:\:{If}\:{any}\:{prime}\:{factor}\:{in}\:{x}\:\left({or}\:{y}\right) \\ $$$${has}\:{exponent}\:\mathrm{0},\:{same}\:{prime}\:{in}\:{y}\left({or}\:{in}\:{x}\right) \\ $$$${has}\:{any}\:{exponent}\:{from}\:{whole}\:{numbers}. \\ $$$${Rule}\mathrm{2}:\:{If}\:{any}\:{prime}\:{has}\:{exponent}\:{other} \\ $$$${than}\:\mathrm{0}\:{in}\:{x}\:\left({or}\:{y}\right),{same}\:{prime}\:{in}\:{y}\left({or}\:{x}\right. \\ $$$${has}\:{same}\:{exponent}. \\ $$$$\mathrm{x}=\mathrm{3}^{\mathrm{2}} .\mathrm{7}^{\mathrm{0}} .\mathrm{2}^{\mathrm{4}} =\mathrm{144} \\ $$$$\mathrm{y}=\mathrm{3}^{\mathrm{2}} .\mathrm{7}^{\mathrm{3}} .\mathrm{2}^{\mathrm{0}} =\mathrm{3087} \\ $$$$ \\ $$$$\:^{\bullet} {exponents}\:{equal} \\ $$$$\:^{\bullet} {exponent}\:\mathrm{0}\:{in}\:{a}\:{primefactor}\:{of}\:\mathrm{x} \\ $$$$\:\:{Any}\:{exponent}\:{in}\:{the}\:\mathrm{same}\:{prime}\:{of}\:\mathrm{y} \\ $$$$\:^{\bullet} {exponent}\:\mathrm{0}\:{in}\:{a}\:{primefactor}\:{of}\:\mathrm{y} \\ $$$$\:\:{Any}\:{exponent}\:{in}\:{the}\:\mathrm{same}\:{prime}\:{of}\:\mathrm{x} \\ $$$$ \\ $$$$\: \\ $$

Commented by Rasheed.Sindhi last updated on 23/Jun/19

Worthless answer of worthless question!

$${Worthless}\:{answer}\:{of}\:{worthless}\:{question}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com