Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 159925 by Rasheed.Sindhi last updated on 22/Nov/21

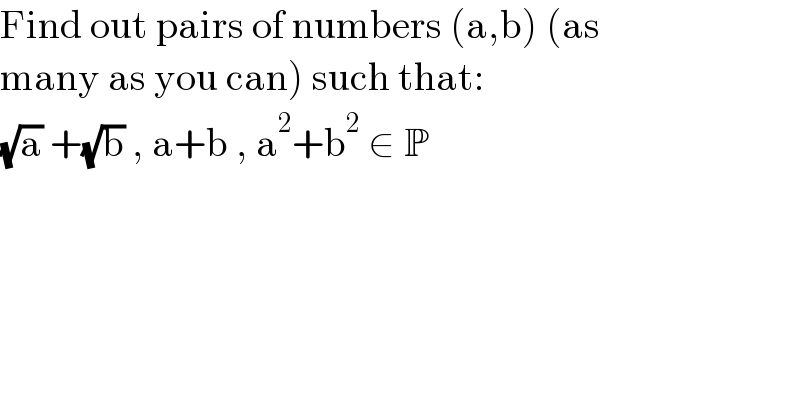
Find out pairs of numbers (a,b) (as many as you can) such that: (√a) +(√b) , a+b , a^2 +b^2 ∈ P

$$\mathrm{Find}\:\mathrm{out}\:\mathrm{pairs}\:\mathrm{of}\:\mathrm{numbers}\:\left(\mathrm{a},\mathrm{b}\right)\:\left(\mathrm{as}\right. \\ $$$$\left.\mathrm{many}\:\mathrm{as}\:\mathrm{you}\:\mathrm{can}\right)\:\mathrm{such}\:\mathrm{that}: \\ $$$$\sqrt{\mathrm{a}}\:+\sqrt{\mathrm{b}}\:,\:\mathrm{a}+\mathrm{b}\:,\:\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} \:\in\:\mathbb{P} \\ $$

Answered by nikif99 last updated on 23/Nov/21

Pairs (a, b) up to 121: (4, 9), (4, 25), (9, 64), (25, 64), (36, 121), (49, 100), (81, 100).

$${Pairs}\:\left({a},\:{b}\right)\:{up}\:{to}\:\mathrm{121}: \\ $$$$\left(\mathrm{4},\:\mathrm{9}\right),\:\left(\mathrm{4},\:\mathrm{25}\right),\:\left(\mathrm{9},\:\mathrm{64}\right),\:\left(\mathrm{25},\:\mathrm{64}\right),\: \\ $$$$\left(\mathrm{36},\:\mathrm{121}\right),\:\left(\mathrm{49},\:\mathrm{100}\right),\:\left(\mathrm{81},\:\mathrm{100}\right). \\ $$

Commented by Rasheed.Sindhi last updated on 23/Nov/21

Thanks sir!

$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{sir}! \\ $$

Commented by Rasheed.Sindhi last updated on 23/Nov/21

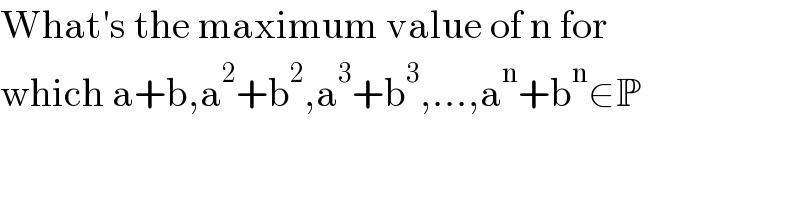
What′s the maximum value of n for which a+b,a^2 +b^2 ,a^3 +b^3 ,...,a^n +b^n ∈P

$$\mathrm{What}'\mathrm{s}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{value}\:\mathrm{of}\:\mathrm{n}\:\mathrm{for} \\ $$$$\mathrm{which}\:\mathrm{a}+\mathrm{b},\mathrm{a}^{\mathrm{2}} +\mathrm{b}^{\mathrm{2}} ,\mathrm{a}^{\mathrm{3}} +\mathrm{b}^{\mathrm{3}} ,...,\mathrm{a}^{\mathrm{n}} +\mathrm{b}^{\mathrm{n}} \in\mathbb{P} \\ $$

Commented by Rasheed.Sindhi last updated on 23/Nov/21

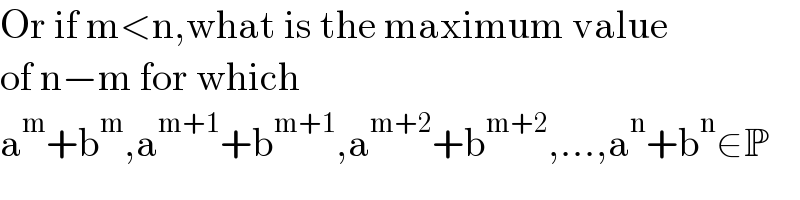
Or if m<n,what is the maximum value of n−m for which a^m +b^m ,a^(m+1) +b^(m+1) ,a^(m+2) +b^(m+2) ,...,a^n +b^n ∈P

$$\mathrm{Or}\:\mathrm{if}\:\mathrm{m}<\mathrm{n},\mathrm{what}\:\mathrm{is}\:\mathrm{the}\:\mathrm{maximum}\:\mathrm{value} \\ $$$$\mathrm{of}\:\mathrm{n}−\mathrm{m}\:\mathrm{for}\:\mathrm{which} \\ $$$$\mathrm{a}^{\mathrm{m}} +\mathrm{b}^{\mathrm{m}} ,\mathrm{a}^{\mathrm{m}+\mathrm{1}} +\mathrm{b}^{\mathrm{m}+\mathrm{1}} ,\mathrm{a}^{\mathrm{m}+\mathrm{2}} +\mathrm{b}^{\mathrm{m}+\mathrm{2}} ,...,\mathrm{a}^{\mathrm{n}} +\mathrm{b}^{\mathrm{n}} \in\mathbb{P} \\ $$

Commented by nikif99 last updated on 23/Nov/21

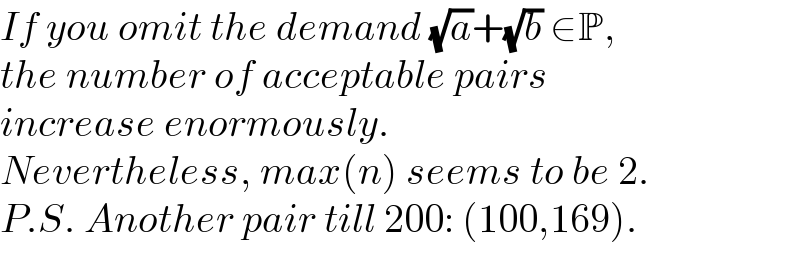
If you omit the demand (√a)+(√b) ∈P, the number of acceptable pairs increase enormously. Nevertheless, max(n) seems to be 2. P.S. Another pair till 200: (100,169).

$${If}\:{you}\:{omit}\:{the}\:{demand}\:\sqrt{{a}}+\sqrt{{b}}\:\in\mathbb{P}, \\ $$$${the}\:{number}\:{of}\:{acceptable}\:{pairs}\: \\ $$$${increase}\:{enormously}. \\ $$$${Nevertheless},\:{max}\left({n}\right)\:{seems}\:{to}\:{be}\:\mathrm{2}. \\ $$$${P}.{S}.\:{Another}\:{pair}\:{till}\:\mathrm{200}:\:\left(\mathrm{100},\mathrm{169}\right). \\ $$

Commented by Rasheed.Sindhi last updated on 23/Nov/21

Thanks a lot sir! You′re right because a^3 +b^3 is always composite. The claim should be: a+b,a^2 +b^2 ,a^4 +b^4 ,a^8 +b^8 ,...∈P Your provided examples are successful upto 3 levels.For example If instead of (100,169) if we consider (a,b)=((√(100)) ,(√(169)) )=(10,13) 10+13=23∈P 10^2 +13^2 =269∈P 10^4 +13^4 =38561∈P Thanks for attention!

$$\mathcal{T}{hanks}\:{a}\:{lot}\:{sir}!\:{You}'{re}\:{right}\:{because} \\ $$$${a}^{\mathrm{3}} +{b}^{\mathrm{3}} \:{is}\:{always}\:{composite}. \\ $$$$\mathcal{T}{he}\:{claim}\:{should}\:{be}: \\ $$$${a}+{b},{a}^{\mathrm{2}} +{b}^{\mathrm{2}} ,{a}^{\mathrm{4}} +{b}^{\mathrm{4}} ,{a}^{\mathrm{8}} +{b}^{\mathrm{8}} ,...\in\mathbb{P} \\ $$$${Your}\:{provided}\:{examples}\:{are}\: \\ $$$${successful}\:{upto}\:\mathrm{3}\:{levels}.{For}\:{example} \\ $$$${If}\:{instead}\:{of}\:\left(\mathrm{100},\mathrm{169}\right)\:{if}\:{we} \\ $$$${consider}\:\left({a},{b}\right)=\left(\sqrt{\mathrm{100}}\:,\sqrt{\mathrm{169}}\:\right)=\left(\mathrm{10},\mathrm{13}\right) \\ $$$$\mathrm{10}+\mathrm{13}=\mathrm{23}\in\mathbb{P} \\ $$$$\mathrm{10}^{\mathrm{2}} +\mathrm{13}^{\mathrm{2}} =\mathrm{269}\in\mathbb{P} \\ $$$$\mathrm{10}^{\mathrm{4}} +\mathrm{13}^{\mathrm{4}} =\mathrm{38561}\in\mathbb{P} \\ $$$$\mathbb{T}\mathrm{han}\Bbbk\mathrm{s}\:\mathrm{for}\:\mathrm{attention}! \\ $$

Commented by nikif99 last updated on 23/Nov/21

Excellent post! Thank you too.

$${Excellent}\:{post}!\:{Thank}\:{you}\:{too}. \\ $$

Commented by Rasheed.Sindhi last updated on 24/Nov/21

��������

Terms of Service

Privacy Policy

Contact: info@tinkutara.com