Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 166475 by Rasheed.Sindhi last updated on 20/Feb/22

Find out n∈N such that n^2 +n is divisible by 30.

$$\mathcal{F}{ind}\:{out}\:{n}\in\mathbb{N} \\ $$$$\:{such}\:{that} \\ $$$${n}^{\mathrm{2}} +{n}\:{is}\:{divisible}\:{by}\:\mathrm{30}. \\ $$

Commented by mr W last updated on 20/Feb/22

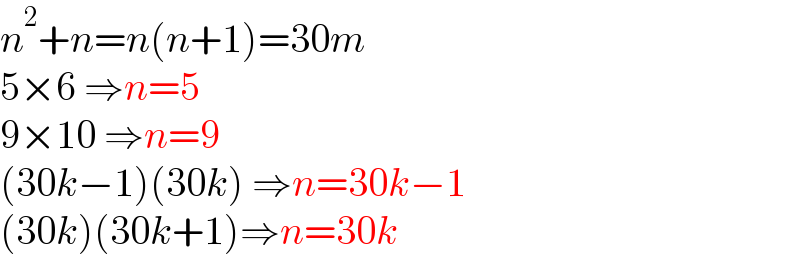
n^2 +n=n(n+1)=30m 5×6 ⇒n=5 9×10 ⇒n=9 (30k−1)(30k) ⇒n=30k−1 (30k)(30k+1)⇒n=30k

$${n}^{\mathrm{2}} +{n}={n}\left({n}+\mathrm{1}\right)=\mathrm{30}{m} \\ $$$$\mathrm{5}×\mathrm{6}\:\Rightarrow{n}=\mathrm{5} \\ $$$$\mathrm{9}×\mathrm{10}\:\Rightarrow{n}=\mathrm{9} \\ $$$$\left(\mathrm{30}{k}−\mathrm{1}\right)\left(\mathrm{30}{k}\right)\:\Rightarrow{n}=\mathrm{30}{k}−\mathrm{1} \\ $$$$\left(\mathrm{30}{k}\right)\left(\mathrm{30}{k}+\mathrm{1}\right)\Rightarrow{n}=\mathrm{30}{k} \\ $$

Commented by mathsmine last updated on 20/Feb/22

n=15 worck also

$${n}=\mathrm{15}\:{worck}\:{also} \\ $$$$ \\ $$

Commented by Rasheed.Sindhi last updated on 21/Feb/22

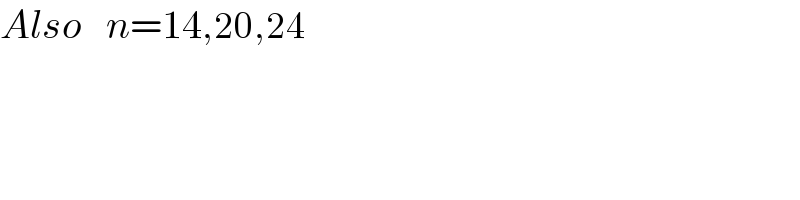
Also n=14,20,24

$${Also}\:\:\:{n}=\mathrm{14},\mathrm{20},\mathrm{24} \\ $$

Commented by Rasheed.Sindhi last updated on 21/Feb/22

ThanX Sirs!

$$\mathcal{T}{han}\mathcal{X}\:\mathcal{S}{irs}! \\ $$

Commented by SANOGO last updated on 21/Feb/22

merci bien

$${merci}\:{bien} \\ $$

Answered by Rasheed.Sindhi last updated on 21/Feb/22

n(n+1)=30k •2∣n ∧ 15∣(n+1) n=2k⇒15∣(2k+1) 2k+1=15m n=2k=15m−1 n=2k=15m−1 determinant (((n=2k=15m−1))) k=((15m−1)/2)∈N n=2( ((15m−1)/2)∈N ) determinant ((m,1,3,5,(...),(2a+1),(...)),(n,(14),(44),(74),(...),(30a+14_(a=0,1,2,...) ),(...))) •3∣n ∧ 10∣(n+1) n=3k⇒10∣(3k+1) 3k+1=10m n=3k=10m−1 determinant (((n=3k=10m−1))) k=((10m−1)/3)∈N n=3(((10m−1)/3)∈N) determinant ((m,1,4,7,(10),(...),(1+3a),(...)),(n,9,(39),(69),(99),(...),(30a+9_(a=0,1,2,...) ),(...))) •5∣n ∧ 6∣(n+1) n=5k⇒6∣(5k+1) 5k+1=6m n=5k=6m−1 determinant (((n=5k=6m−1))) k=((6m−1)/5)∈N n=5(((6m−1)/5)∈N) determinant ((m,1,6,(11),(...),(5a+1),(...)),(n,5,(35),(65),(...),(30a+5_(a=0,1,2,...) ),(...))) •6∣n ∧ 5∣(n+1) n=6k⇒5∣(6k+1) 6k+1=5m n=6k=5m−1 determinant (((n=6k=5m−1))) k=((5m−1)/6)∈N n=6(((5m−1)/6)∈N) determinant ((m,5,(11),(17),(...),(6a+5),(...)),(n,(24),(54),(84),(...),(30a+24),(...))) •10∣n ∧ 3∣(n+1) n=10k⇒3∣(10k+1) 10k+1=3m n=10k=3m−1 determinant (((n=10k=3m−1))) k=((3m−1)/(10))∈N n=10(((3m−1)/(10))∈N) determinant ((m,7,(17),(27),(...),(10a+7),(...)),(n,(20),(50),(80),(...),(30a+ 2_(a=0,1,2,...) 0),(...))) •15∣n ∧ 2∣(n+1) n=15k⇒2∣(15k+1) 15k+1=2m n=15k=2m−1 determinant (((n=15k=2m−1))) k=((2m−1)/(15))∈N n=15(((2m−1)/(15))∈N) determinant ((m,8,(23),(38),(...),(15a+8),(...)),(n,(15),(45),(75),(...),(30a+15_(a=0,1,2,...) ),(...))) •30∣n n=30a determinant ((0,(30),(60),(90),(...),(30a),(...))) •30∣(n+1) n+1=30a⇒n=30a−1⇒n=30a+29 determinant (((29),(59),(89),(...),(3a+29),(...))) n=30a , 30a+5 , 30a+9 , 30a+14 , 30a+15 , 30a+20 , 30a+24 , 30a+29 Where a=0,1,2,...

$${n}\left({n}+\mathrm{1}\right)=\mathrm{30}{k} \\ $$$$\bullet\mathrm{2}\mid{n}\:\wedge\:\mathrm{15}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}=\mathrm{2}{k}\Rightarrow\mathrm{15}\mid\left(\mathrm{2}{k}+\mathrm{1}\right) \\ $$$$\mathrm{2}{k}+\mathrm{1}=\mathrm{15}{m} \\ $$$${n}=\mathrm{2}{k}=\mathrm{15}{m}−\mathrm{1} \\ $$$${n}=\mathrm{2}{k}=\mathrm{15}{m}−\mathrm{1} \\ $$$$\begin{array}{|c|}{{n}=\mathrm{2}{k}=\mathrm{15}{m}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:{k}=\frac{\mathrm{15}{m}−\mathrm{1}}{\mathrm{2}}\in\mathbb{N} \\ $$$${n}=\mathrm{2}\left(\:\frac{\mathrm{15}{m}−\mathrm{1}}{\mathrm{2}}\in\mathbb{N}\:\right) \\ $$$$\begin{array}{|c|c|}{{m}}&\hline{\mathrm{1}}&\hline{\mathrm{3}}&\hline{\mathrm{5}}&\hline{...}&\hline{\mathrm{2}{a}+\mathrm{1}}&\hline{...}\\{{n}}&\hline{\mathrm{14}}&\hline{\mathrm{44}}&\hline{\mathrm{74}}&\hline{...}&\hline{\underset{{a}=\mathrm{0},\mathrm{1},\mathrm{2},...} {\mathrm{30}{a}+\mathrm{14}}}&\hline{...}\\\hline\end{array} \\ $$$$\bullet\mathrm{3}\mid{n}\:\wedge\:\mathrm{10}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}=\mathrm{3}{k}\Rightarrow\mathrm{10}\mid\left(\mathrm{3}{k}+\mathrm{1}\right) \\ $$$$\mathrm{3}{k}+\mathrm{1}=\mathrm{10}{m} \\ $$$${n}=\mathrm{3}{k}=\mathrm{10}{m}−\mathrm{1} \\ $$$$\begin{array}{|c|}{{n}=\mathrm{3}{k}=\mathrm{10}{m}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:{k}=\frac{\mathrm{10}{m}−\mathrm{1}}{\mathrm{3}}\in\mathbb{N} \\ $$$$\:\:\:{n}=\mathrm{3}\left(\frac{\mathrm{10}{m}−\mathrm{1}}{\mathrm{3}}\in\mathbb{N}\right) \\ $$$$\begin{array}{|c|c|}{{m}}&\hline{\mathrm{1}}&\hline{\mathrm{4}}&\hline{\mathrm{7}}&\hline{\mathrm{10}}&\hline{...}&\hline{\mathrm{1}+\mathrm{3}{a}}&\hline{...}\\{{n}}&\hline{\mathrm{9}}&\hline{\mathrm{39}}&\hline{\mathrm{69}}&\hline{\mathrm{99}}&\hline{...}&\hline{\underset{{a}=\mathrm{0},\mathrm{1},\mathrm{2},...} {\mathrm{30}{a}+\mathrm{9}}}&\hline{...}\\\hline\end{array} \\ $$$$\bullet\mathrm{5}\mid{n}\:\wedge\:\mathrm{6}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}=\mathrm{5}{k}\Rightarrow\mathrm{6}\mid\left(\mathrm{5}{k}+\mathrm{1}\right) \\ $$$$\mathrm{5}{k}+\mathrm{1}=\mathrm{6}{m} \\ $$$${n}=\mathrm{5}{k}=\mathrm{6}{m}−\mathrm{1} \\ $$$$\begin{array}{|c|}{{n}=\mathrm{5}{k}=\mathrm{6}{m}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\:{k}=\frac{\mathrm{6}{m}−\mathrm{1}}{\mathrm{5}}\in\mathbb{N} \\ $$$${n}=\mathrm{5}\left(\frac{\mathrm{6}{m}−\mathrm{1}}{\mathrm{5}}\in\mathbb{N}\right) \\ $$$$\begin{array}{|c|c|}{{m}}&\hline{\mathrm{1}}&\hline{\mathrm{6}}&\hline{\mathrm{11}}&\hline{...}&\hline{\mathrm{5}{a}+\mathrm{1}}&\hline{...}\\{{n}}&\hline{\mathrm{5}}&\hline{\mathrm{35}}&\hline{\mathrm{65}}&\hline{...}&\hline{\underset{{a}=\mathrm{0},\mathrm{1},\mathrm{2},...} {\mathrm{30}{a}+\mathrm{5}}}&\hline{...}\\\hline\end{array} \\ $$$$\bullet\mathrm{6}\mid{n}\:\wedge\:\mathrm{5}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}=\mathrm{6}{k}\Rightarrow\mathrm{5}\mid\left(\mathrm{6}{k}+\mathrm{1}\right) \\ $$$$\mathrm{6}{k}+\mathrm{1}=\mathrm{5}{m} \\ $$$${n}=\mathrm{6}{k}=\mathrm{5}{m}−\mathrm{1} \\ $$$$\begin{array}{|c|}{{n}=\mathrm{6}{k}=\mathrm{5}{m}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:{k}=\frac{\mathrm{5}{m}−\mathrm{1}}{\mathrm{6}}\in\mathbb{N} \\ $$$${n}=\mathrm{6}\left(\frac{\mathrm{5}{m}−\mathrm{1}}{\mathrm{6}}\in\mathbb{N}\right) \\ $$$$\begin{array}{|c|c|}{{m}}&\hline{\mathrm{5}}&\hline{\mathrm{11}}&\hline{\mathrm{17}}&\hline{...}&\hline{\mathrm{6}{a}+\mathrm{5}}&\hline{...}\\{{n}}&\hline{\mathrm{24}}&\hline{\mathrm{54}}&\hline{\mathrm{84}}&\hline{...}&\hline{\mathrm{30}{a}+\mathrm{24}}&\hline{...}\\\hline\end{array} \\ $$$$\bullet\mathrm{10}\mid{n}\:\wedge\:\mathrm{3}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}=\mathrm{10}{k}\Rightarrow\mathrm{3}\mid\left(\mathrm{10}{k}+\mathrm{1}\right) \\ $$$$\mathrm{10}{k}+\mathrm{1}=\mathrm{3}{m} \\ $$$${n}=\mathrm{10}{k}=\mathrm{3}{m}−\mathrm{1} \\ $$$$\begin{array}{|c|}{{n}=\mathrm{10}{k}=\mathrm{3}{m}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{k}=\frac{\mathrm{3}{m}−\mathrm{1}}{\mathrm{10}}\in\mathbb{N} \\ $$$$\:\:\:\:{n}=\mathrm{10}\left(\frac{\mathrm{3}{m}−\mathrm{1}}{\mathrm{10}}\in\mathbb{N}\right) \\ $$$$\begin{array}{|c|c|}{{m}}&\hline{\mathrm{7}}&\hline{\mathrm{17}}&\hline{\mathrm{27}}&\hline{...}&\hline{\mathrm{10}{a}+\mathrm{7}}&\hline{...}\\{{n}}&\hline{\mathrm{20}}&\hline{\mathrm{50}}&\hline{\mathrm{80}}&\hline{...}&\hline{\underset{{a}=\mathrm{0},\mathrm{1},\mathrm{2},...} {\mathrm{30}{a}+\:\mathrm{2}0}}&\hline{...}\\\hline\end{array} \\ $$$$\bullet\mathrm{15}\mid{n}\:\wedge\:\mathrm{2}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}=\mathrm{15}{k}\Rightarrow\mathrm{2}\mid\left(\mathrm{15}{k}+\mathrm{1}\right) \\ $$$$\mathrm{15}{k}+\mathrm{1}=\mathrm{2}{m} \\ $$$${n}=\mathrm{15}{k}=\mathrm{2}{m}−\mathrm{1} \\ $$$$\begin{array}{|c|}{{n}=\mathrm{15}{k}=\mathrm{2}{m}−\mathrm{1}}\\\hline\end{array} \\ $$$$\:\:\:\:\:\:\:\:{k}=\frac{\mathrm{2}{m}−\mathrm{1}}{\mathrm{15}}\in\mathbb{N} \\ $$$$\:\:\:\:\:{n}=\mathrm{15}\left(\frac{\mathrm{2}{m}−\mathrm{1}}{\mathrm{15}}\in\mathbb{N}\right) \\ $$$$\begin{array}{|c|c|}{{m}}&\hline{\mathrm{8}}&\hline{\mathrm{23}}&\hline{\mathrm{38}}&\hline{...}&\hline{\mathrm{15}{a}+\mathrm{8}}&\hline{...}\\{{n}}&\hline{\mathrm{15}}&\hline{\mathrm{45}}&\hline{\mathrm{75}}&\hline{...}&\hline{\underset{{a}=\mathrm{0},\mathrm{1},\mathrm{2},...} {\mathrm{30}{a}+\mathrm{15}}}&\hline{...}\\\hline\end{array} \\ $$$$\bullet\mathrm{30}\mid{n}\: \\ $$$$\:\:\:{n}=\mathrm{30}{a} \\ $$$$\begin{array}{|c|}{\mathrm{0}}&\hline{\mathrm{30}}&\hline{\mathrm{60}}&\hline{\mathrm{90}}&\hline{...}&\hline{\mathrm{30}{a}}&\hline{...}\\\hline\end{array}\: \\ $$$$\bullet\mathrm{30}\mid\left({n}+\mathrm{1}\right) \\ $$$${n}+\mathrm{1}=\mathrm{30}{a}\Rightarrow{n}=\mathrm{30}{a}−\mathrm{1}\Rightarrow{n}=\mathrm{30}{a}+\mathrm{29} \\ $$$$\begin{array}{|c|}{\mathrm{29}}&\hline{\mathrm{59}}&\hline{\mathrm{89}}&\hline{...}&\hline{\mathrm{3}{a}+\mathrm{29}}&\hline{...}\\\hline\end{array} \\ $$$$ \\ $$$${n}=\mathrm{30}{a}\:,\:\mathrm{30}{a}+\mathrm{5}\:,\:\mathrm{30}{a}+\mathrm{9}\:,\:\mathrm{30}{a}+\mathrm{14}\:, \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{30}{a}+\mathrm{15}\:,\:\mathrm{30}{a}+\mathrm{20}\:,\:\mathrm{30}{a}+\mathrm{24}\:,\:\mathrm{30}{a}+\mathrm{29}\:\: \\ $$$$\:\:\:\:\:\:\:{Where}\:{a}=\mathrm{0},\mathrm{1},\mathrm{2},... \\ $$

Commented by Rasheed.Sindhi last updated on 21/Feb/22

You′re welcome!

$${You}'{re}\:{welcome}! \\ $$

Commented by SANOGO last updated on 21/Feb/22

merci bien

$${merci}\:{bien} \\ $$

Answered by Rasheed.Sindhi last updated on 21/Feb/22

n^2 +n≡0[30]⇒n^2 ≡−n[30] ⇒n^2 ≡30−n[30] determinant ((n,(n^2 [30]),((30−n)[30])),(0,0,0),(1,1,(29)),(2,4,(28)),(3,9,(27)),(4,(16),(26)),(5,(25),(25)),(6,6,(24)),(7,(19),(23)),(8,4,(22)),(9,(21),(21)),((10),(10),(20)),((11),1,(19)),((12),(24),(18)),((13),(19),(17)),((14),(16),(16)),((15),(15),(15)),((16),(19),(14)),((17),(19),(13)),((18),(24),(12)),((19),1,(11)),((20),(10),(10)),((21),(21),9),((22),4,8),((23),(19),7),((24),6,6),((25),(25),5),((26),(16),4),((27),9,3),((28),4,2),((29),1,1)) n=0,5,9,14,15,20,24,29 In general: 30k,30k+5,30k+9,30k+14, 30k+15,30k+20,30k+24,30k+29 for k=0,1,2,...

$${n}^{\mathrm{2}} +{n}\equiv\mathrm{0}\left[\mathrm{30}\right]\Rightarrow{n}^{\mathrm{2}} \equiv−{n}\left[\mathrm{30}\right] \\ $$$$\Rightarrow{n}^{\mathrm{2}} \equiv\mathrm{30}−{n}\left[\mathrm{30}\right] \\ $$$$\begin{array}{|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|c|}{{n}}&\hline{{n}^{\mathrm{2}} \left[\mathrm{30}\right]}&\hline{\left(\mathrm{30}−{n}\right)\left[\mathrm{30}\right]}\\{\underline{\mathrm{0}}}&\hline{\mathrm{0}}&\hline{\mathrm{0}}\\{\mathrm{1}}&\hline{\mathrm{1}}&\hline{\mathrm{29}}\\{\mathrm{2}}&\hline{\mathrm{4}}&\hline{\mathrm{28}}\\{\mathrm{3}}&\hline{\mathrm{9}}&\hline{\mathrm{27}}\\{\mathrm{4}}&\hline{\mathrm{16}}&\hline{\mathrm{26}}\\{\underline{\mathrm{5}}}&\hline{\mathrm{25}}&\hline{\mathrm{25}}\\{\mathrm{6}}&\hline{\mathrm{6}}&\hline{\mathrm{24}}\\{\mathrm{7}}&\hline{\mathrm{19}}&\hline{\mathrm{23}}\\{\mathrm{8}}&\hline{\mathrm{4}}&\hline{\mathrm{22}}\\{\underline{\mathrm{9}}}&\hline{\mathrm{21}}&\hline{\mathrm{21}}\\{\mathrm{10}}&\hline{\mathrm{10}}&\hline{\mathrm{20}}\\{\mathrm{11}}&\hline{\mathrm{1}}&\hline{\mathrm{19}}\\{\mathrm{12}}&\hline{\mathrm{24}}&\hline{\mathrm{18}}\\{\mathrm{13}}&\hline{\mathrm{19}}&\hline{\mathrm{17}}\\{\underline{\mathrm{14}}}&\hline{\mathrm{16}}&\hline{\mathrm{16}}\\{\underline{\mathrm{15}}}&\hline{\mathrm{15}}&\hline{\mathrm{15}}\\{\mathrm{16}}&\hline{\mathrm{19}}&\hline{\mathrm{14}}\\{\mathrm{17}}&\hline{\mathrm{19}}&\hline{\mathrm{13}}\\{\mathrm{18}}&\hline{\mathrm{24}}&\hline{\mathrm{12}}\\{\mathrm{19}}&\hline{\mathrm{1}}&\hline{\mathrm{11}}\\{\underline{\mathrm{20}}}&\hline{\mathrm{10}}&\hline{\mathrm{10}}\\{\mathrm{21}}&\hline{\mathrm{21}}&\hline{\mathrm{9}}\\{\mathrm{22}}&\hline{\mathrm{4}}&\hline{\mathrm{8}}\\{\mathrm{23}}&\hline{\mathrm{19}}&\hline{\mathrm{7}}\\{\underline{\mathrm{24}}}&\hline{\mathrm{6}}&\hline{\mathrm{6}}\\{\mathrm{25}}&\hline{\mathrm{25}}&\hline{\mathrm{5}}\\{\mathrm{26}}&\hline{\mathrm{16}}&\hline{\mathrm{4}}\\{\mathrm{27}}&\hline{\mathrm{9}}&\hline{\mathrm{3}}\\{\mathrm{28}}&\hline{\mathrm{4}}&\hline{\mathrm{2}}\\{\underline{\mathrm{29}}}&\hline{\mathrm{1}}&\hline{\mathrm{1}}\\\hline\end{array} \\ $$$${n}=\mathrm{0},\mathrm{5},\mathrm{9},\mathrm{14},\mathrm{15},\mathrm{20},\mathrm{24},\mathrm{29} \\ $$$${In}\:{general}: \\ $$$$\mathrm{30}{k},\mathrm{30}{k}+\mathrm{5},\mathrm{30}{k}+\mathrm{9},\mathrm{30}{k}+\mathrm{14}, \\ $$$$\mathrm{30}{k}+\mathrm{15},\mathrm{30}{k}+\mathrm{20},\mathrm{30}{k}+\mathrm{24},\mathrm{30}{k}+\mathrm{29} \\ $$$${for}\:{k}=\mathrm{0},\mathrm{1},\mathrm{2},... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com