
Question Number 99300 by mr W last updated on 20/Jun/20
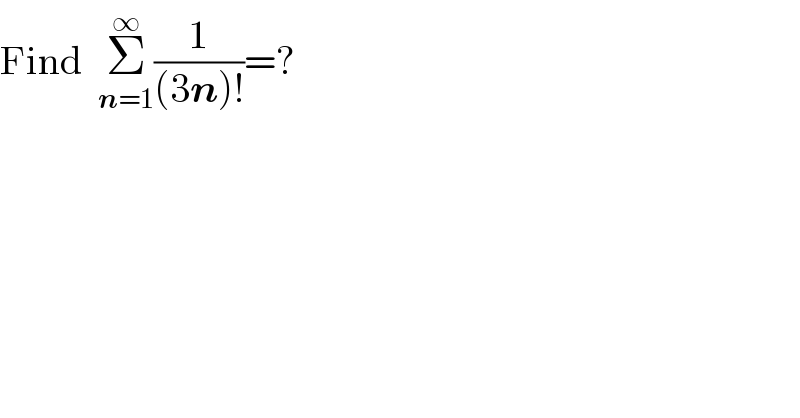
$$\mathrm{Find}\:\:\underset{\boldsymbol{{n}}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{3}\boldsymbol{{n}}\right)!}=? \\ $$
Answered by maths mind last updated on 20/Jun/20

$${Z}^{\mathrm{3}} −\mathrm{1}=\mathrm{0}\Rightarrow{z}\in\left\{\mathrm{1},{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} ,{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} \right\} \\ $$$${e}^{{z}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{{z}^{{n}} }{{n}!},{a}={e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} ,{b}={e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} ,{c}=\mathrm{1} \\ $$$${e}^{{a}} +{e}^{{b}} +{e}^{{c}} =\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}+{e}^{\frac{\mathrm{2}{in}\pi}{\mathrm{3}}} +{e}^{\frac{\mathrm{4}{in}\pi}{\mathrm{3}}} }{{n}!} \\ $$$$=\underset{{j}=\mathrm{0}} {\overset{\mathrm{2}} {\sum}}.\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}+{e}^{\frac{\mathrm{2}{i}\left(\mathrm{3}{n}+{j}\right)\pi}{\mathrm{3}}} +{e}^{\frac{\mathrm{4}{i}\left(\mathrm{3}{n}+{j}\right)\pi}{\mathrm{3}}} }{\left(\mathrm{3}{n}+{j}\right)!} \\ $$$$=\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{3}}{\left(\mathrm{3}{n}\right)!}+\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}+{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} +{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} }{\left(\mathrm{3}{n}+\mathrm{1}\right)!}+\Sigma\frac{\mathrm{1}+{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} +{e}^{\frac{\mathrm{8}{i}\pi}{\mathrm{3}}} }{\left(\mathrm{3}{n}+\mathrm{2}\right)!} \\ $$$$\mathrm{1}+{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} +{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} =\mathrm{0},\frac{\mathrm{8}\pi}{\mathrm{3}}=\mathrm{2}\pi+\frac{\mathrm{2}\pi}{\mathrm{3}}\Rightarrow\mathrm{1}+{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} +{e}^{\frac{\mathrm{8}\pi}{\mathrm{3}}{i}} =\mathrm{0} \\ $$$$\Rightarrow{e}+{e}^{{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} } +{e}^{{e}^{\frac{\mathrm{4}{i}\pi}{\mathrm{3}}} } =\mathrm{3}\underset{{n}\geqslant\mathrm{0}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}=\mathrm{3}\left(\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}+\mathrm{1}\right) \\ $$$$\underset{{n}\geqslant\mathrm{1}} {\sum}\frac{\mathrm{1}}{\left(\mathrm{3}{n}\right)!}=\frac{{e}+{e}^{{e}^{\frac{\mathrm{2}{i}\pi}{\mathrm{3}}} } +{e}^{{e}^{\mathrm{4}\frac{{i}\pi}{\mathrm{3}}} } }{\mathrm{3}}−\mathrm{1} \\ $$
Commented by mr W last updated on 20/Jun/20
$${thanks}\:{sir}!\:{let}\:{me}\:{study}! \\ $$
Commented by maths mind last updated on 20/Jun/20
$${nice}\:{day}\:\:{sir}\:\:{withe}\:{pleasur} \\ $$
