
Question Number 188806 by horsebrand11 last updated on 07/Mar/23
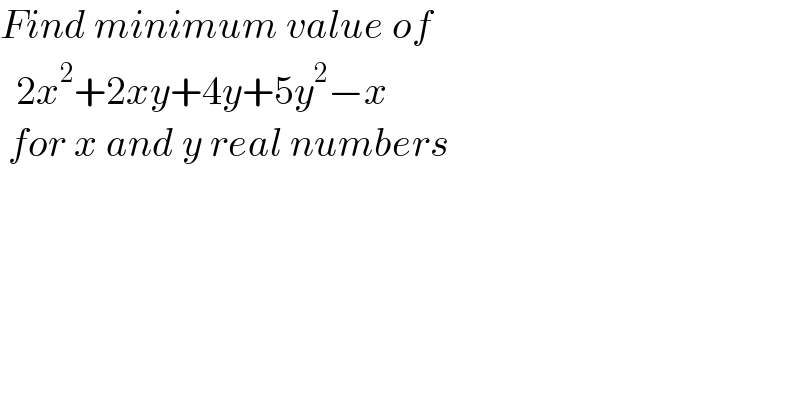
$${Find}\:{minimum}\:{value}\:{of}\: \\ $$$$\:\:\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{4}{y}+\mathrm{5}{y}^{\mathrm{2}} −{x}\: \\ $$$$\:{for}\:{x}\:{and}\:{y}\:{real}\:{numbers} \\ $$
Answered by mr W last updated on 07/Mar/23
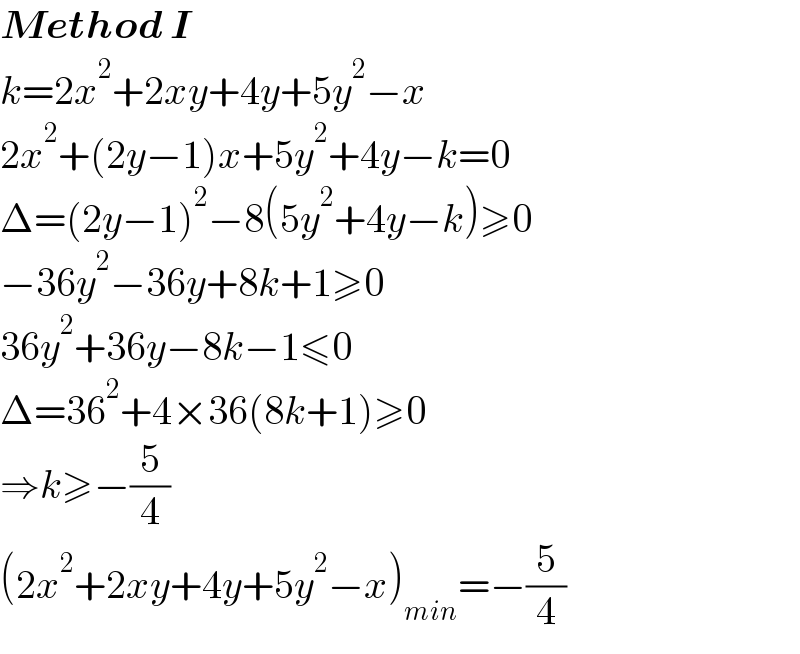
$$\boldsymbol{{Method}}\:\boldsymbol{{I}} \\ $$$${k}=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{4}{y}+\mathrm{5}{y}^{\mathrm{2}} −{x} \\ $$$$\mathrm{2}{x}^{\mathrm{2}} +\left(\mathrm{2}{y}−\mathrm{1}\right){x}+\mathrm{5}{y}^{\mathrm{2}} +\mathrm{4}{y}−{k}=\mathrm{0} \\ $$$$\Delta=\left(\mathrm{2}{y}−\mathrm{1}\right)^{\mathrm{2}} −\mathrm{8}\left(\mathrm{5}{y}^{\mathrm{2}} +\mathrm{4}{y}−{k}\right)\geqslant\mathrm{0} \\ $$$$−\mathrm{36}{y}^{\mathrm{2}} −\mathrm{36}{y}+\mathrm{8}{k}+\mathrm{1}\geqslant\mathrm{0} \\ $$$$\mathrm{36}{y}^{\mathrm{2}} +\mathrm{36}{y}−\mathrm{8}{k}−\mathrm{1}\leqslant\mathrm{0} \\ $$$$\Delta=\mathrm{36}^{\mathrm{2}} +\mathrm{4}×\mathrm{36}\left(\mathrm{8}{k}+\mathrm{1}\right)\geqslant\mathrm{0} \\ $$$$\Rightarrow{k}\geqslant−\frac{\mathrm{5}}{\mathrm{4}} \\ $$$$\left(\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{4}{y}+\mathrm{5}{y}^{\mathrm{2}} −{x}\right)_{{min}} =−\frac{\mathrm{5}}{\mathrm{4}} \\ $$
Answered by mr W last updated on 07/Mar/23

$$\boldsymbol{{Method}}\:\boldsymbol{{II}} \\ $$$${k}=\mathrm{2}{x}^{\mathrm{2}} +\mathrm{2}{xy}+\mathrm{4}{y}+\mathrm{5}{y}^{\mathrm{2}} −{x} \\ $$$$\frac{\partial{k}}{\partial{x}}=\mathrm{4}{x}+\mathrm{2}{y}−\mathrm{1}=\mathrm{0}\:\:\:...\left({i}\right) \\ $$$$\frac{\partial{k}}{\partial{y}}=\mathrm{2}{x}+\mathrm{4}+\mathrm{10}{y}=\mathrm{0}\:\:\:...\left({ii}\right) \\ $$$$\Rightarrow{x}=\frac{\mathrm{1}}{\mathrm{2}},\:{y}=−\frac{\mathrm{1}}{\mathrm{2}} \\ $$$${k}_{{min}} =\mathrm{2}×\frac{\mathrm{1}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}−\mathrm{2}+\frac{\mathrm{5}}{\mathrm{4}}−\frac{\mathrm{1}}{\mathrm{2}}=−\frac{\mathrm{5}}{\mathrm{4}}\:\checkmark \\ $$$$\left({it}'{s}\:{minimum},\:{because}\:\frac{\partial^{\mathrm{2}} {k}}{\partial{x}^{\mathrm{2}} }>\mathrm{0},\:\frac{\partial^{\mathrm{2}} {k}}{\partial{y}^{\mathrm{2}} }>\mathrm{0}\right) \\ $$
Commented by ARUNG_Brandon_MBU last updated on 07/Mar/23
Sir can you check my reply on your comment in Q188362
Commented by mr W last updated on 07/Mar/23
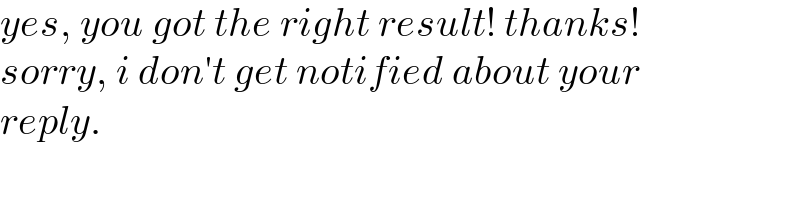
$${yes},\:{you}\:{got}\:{the}\:{right}\:{result}!\:{thanks}! \\ $$$${sorry},\:{i}\:{don}'{t}\:{get}\:{notified}\:{about}\:{your} \\ $$$${reply}. \\ $$
Commented by ARUNG_Brandon_MBU last updated on 07/Mar/23

$$\mathrm{OK}\:\mathrm{Sir}. \\ $$$$\mathrm{Me}\:\mathrm{too}.\:\mathrm{I}\:\mathrm{don}'\mathrm{t}\:\mathrm{get}\:\mathrm{notified}\:\mathrm{about}\:\mathrm{replies}. \\ $$
Commented by mr W last updated on 08/Mar/23
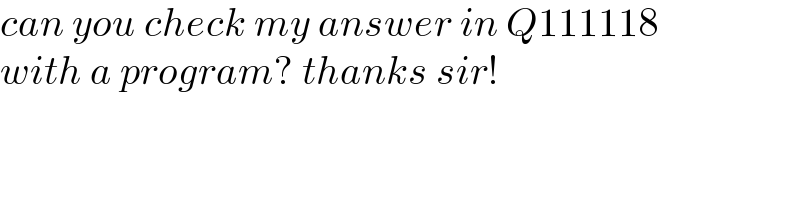
$${can}\:{you}\:{check}\:{my}\:{answer}\:{in}\:{Q}\mathrm{111118} \\ $$$${with}\:{a}\:{program}?\:{thanks}\:{sir}! \\ $$
Commented by ARUNG_Brandon_MBU last updated on 09/Mar/23
The system says "Question deleted from forum."
Commented by mr W last updated on 09/Mar/23

$${sorry}\:{the}\:{question}\:#\:{is}\:\mathrm{188879}. \\ $$$${i}\:{mistook}\:{the}\:{ID}\:{of}\:{that}\:{user}\:{for}\:{the} \\ $$$${question}\:{number}. \\ $$
