
Question Number 31707 by gunawan last updated on 13/Mar/18
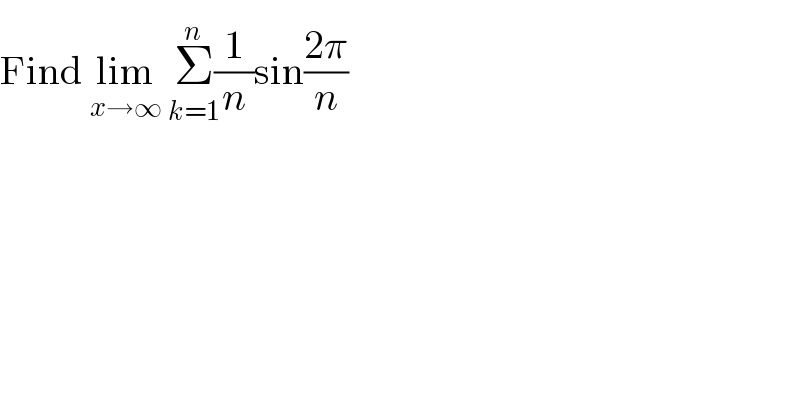
$$\mathrm{Find}\:\underset{{x}\rightarrow\infty} {\mathrm{lim}}\:\underset{{k}=\mathrm{1}} {\overset{{n}} {\Sigma}}\frac{\mathrm{1}}{{n}}\mathrm{sin}\frac{\mathrm{2}\pi}{{n}}\: \\ $$
Commented by abdo imad last updated on 18/Mar/18
![i think the Q.is find lim_(n→∞) Σ_(k=1) ^n (1/n) sin(((2kπ)/n)) let put S_n =Σ_(k=1) ^n (1/n)sin(((2kπ)/n)) we have S_n =(1/(2π)) ((2π)/n) Σ_(k=1) ^n sin(k ((2π)/n))→(1/(2π)) ∫_0 ^(2π) sinx dx =(1/(2π))[−cosx]_0 ^(2π) =0 ⇒lim_(n→∞) S_n =0](Q31994.png)
$${i}\:{think}\:{the}\:{Q}.{is}\:{find}\:{lim}_{{n}\rightarrow\infty} \:\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{n}}\:{sin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right) \\ $$$${let}\:{put}\:{S}_{{n}} =\sum_{{k}=\mathrm{1}} ^{{n}} \:\frac{\mathrm{1}}{{n}}{sin}\left(\frac{\mathrm{2}{k}\pi}{{n}}\right)\:{we}\:{have} \\ $$$${S}_{{n}} =\frac{\mathrm{1}}{\mathrm{2}\pi}\:\frac{\mathrm{2}\pi}{{n}}\:\sum_{{k}=\mathrm{1}} ^{{n}} \:{sin}\left({k}\:\frac{\mathrm{2}\pi}{{n}}\right)\rightarrow\frac{\mathrm{1}}{\mathrm{2}\pi}\:\int_{\mathrm{0}} ^{\mathrm{2}\pi} \:{sinx}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}\pi}\left[−{cosx}\right]_{\mathrm{0}} ^{\mathrm{2}\pi} \:\:=\mathrm{0}\:\Rightarrow{lim}_{{n}\rightarrow\infty} \:{S}_{{n}} =\mathrm{0} \\ $$
