
Question Number 62571 by Joel122 last updated on 23/Jun/19
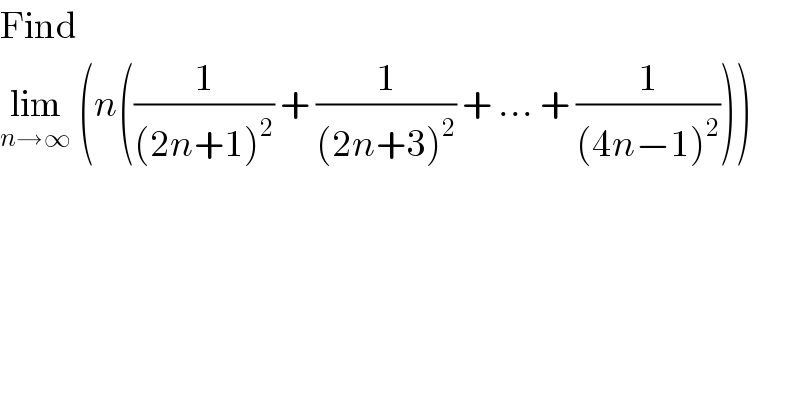
$$\mathrm{Find} \\ $$$$\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:\left({n}\left(\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{1}\right)^{\mathrm{2}} }\:+\:\frac{\mathrm{1}}{\left(\mathrm{2}{n}+\mathrm{3}\right)^{\mathrm{2}} }\:+\:...\:+\:\frac{\mathrm{1}}{\left(\mathrm{4}{n}−\mathrm{1}\right)^{\mathrm{2}} }\right)\right) \\ $$
Commented by Prithwish sen last updated on 23/Jun/19
![lim_(n→∞) (1/n) [(l/((2+(1/n))^2 ))+(1/((2+(3/n))^2 )) +....+(1/((2+((2n−1)/n))^2 ))] = lim_(n→∞) (1/n)Σ_(r=1) ^n (1/((2+((2r−1)/n))^2 )) Putn=(1/h) n→∞ ⇒h→0 = lim_(h→0) h Σ_(r=1) ^n (1/((2+2rh)^2 )) =∫_0 ^1 (dx/((2+2x)^2 )) ∵nh=1=1−0 = (1/4)[−(1/((1+x)))]_0 ^1 =(1/4)[−(1/2)+1] =(1/8)](Q62594.png)
$$\mathrm{li}\underset{\mathrm{n}\rightarrow\infty} {\mathrm{m}}\frac{\mathrm{1}}{\mathrm{n}}\:\left[\frac{\mathrm{l}}{\left(\mathrm{2}+\frac{\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{3}}{\mathrm{n}}\right)^{\mathrm{2}} }\:+....+\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{2n}−\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{2}} }\right] \\ $$$$=\:\mathrm{lim}_{\mathrm{n}\rightarrow\infty} \frac{\mathrm{1}}{\mathrm{n}}\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{2r}−\mathrm{1}}{\mathrm{n}}\right)^{\mathrm{2}} } \\ $$$$\mathrm{Putn}=\frac{\mathrm{1}}{\mathrm{h}}\:\mathrm{n}\rightarrow\infty\:\Rightarrow\mathrm{h}\rightarrow\mathrm{0}\: \\ $$$$=\:\mathrm{lim}_{\mathrm{h}\rightarrow\mathrm{0}} \mathrm{h}\:\underset{\mathrm{r}=\mathrm{1}} {\overset{\mathrm{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}+\mathrm{2rh}\right)^{\mathrm{2}} } \\ $$$$=\underset{\mathrm{0}} {\overset{\mathrm{1}} {\int}}\:\frac{\mathrm{dx}}{\left(\mathrm{2}+\mathrm{2x}\right)^{\mathrm{2}} }\:\:\:\:\because\mathrm{nh}=\mathrm{1}=\mathrm{1}−\mathrm{0} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{4}}\left[−\frac{\mathrm{1}}{\left(\mathrm{1}+\mathrm{x}\right)}\right]_{\mathrm{0}} ^{\mathrm{1}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left[−\frac{\mathrm{1}}{\mathrm{2}}+\mathrm{1}\right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by Joel122 last updated on 23/Jun/19

$$\mathrm{The}\:\mathrm{answer}\:\mathrm{is}\:\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by Tony Lin last updated on 23/Jun/19
![=lim_(n→∞) ((1/2)×(2/n)((1/((2+(1/n))^2 ))+(1/((2+(3/n))^2 ))+...+(1/((4−(1/n))^2 )))) =(1/2)∫_2 ^4 (1/x^2 )dx =(1/2)[−(1/x)]_2 ^4 =−(1/8)+(1/4) =(1/8)](Q62582.png)
$$=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{{n}}\left(\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} }+\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{3}}{{n}}\right)^{\mathrm{2}} }+...+\frac{\mathrm{1}}{\left(\mathrm{4}−\frac{\mathrm{1}}{{n}}\right)^{\mathrm{2}} }\right)\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int_{\mathrm{2}} ^{\mathrm{4}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\left[−\frac{\mathrm{1}}{{x}}\right]_{\mathrm{2}} ^{\mathrm{4}} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{8}}+\frac{\mathrm{1}}{\mathrm{4}} \\ $$$$=\frac{\mathrm{1}}{\mathrm{8}} \\ $$
Commented by JDamian last updated on 23/Jun/19

$${Please},\:{would}\:{you}\:{mind}\:{to}\:{explain}\:{how}\:{the}\:{sum} \\ $$$${of}\:{a}\:{discrete}\:{sucession}\:{turns}\:{into}\:{an}\:{integral} \\ $$$${in}\:\Re? \\ $$
Commented by Tony Lin last updated on 23/Jun/19
![The definite integral of a continuous function f(x) over the interval[a , b] ,denoted by ∫_a ^b f(x)dx, is the limit of Riemann sum as the number of subdivisions approaches infinity i.e ∫_a ^b f(x)dx=lim_(n→∞) Σ_(k=1) ^n △xf(x_k ) where △x=((b−a)/n) and x_k =a+k△x now we have △x=(2/n) , means the constant width of the rectangle, and x_k is the x value of the right edge of the k^(th) rectangle,from x_1 =2+(1/n) to x_n = 4−(1/n) ,then f(x_k ) will give us the height of each rectangle ,and here f(x)=(1/x^2 ) , so the area of the k^(th) rectangle is (2/n)×(1/((2+(2/n)k)^2 )) , and we sum that for values of k from 1 to n R(n)=lim_(n→∞) Σ_(k=1) ^n (1/((2+(2/n)k)^2 ))×(2/n) now we can represent the actual area as a limit: ∫_(2 ) ^4 (1/x^2 )dx=lim_(n→∞) Σ_(k=1) ^n (1/((2+(2/n)k)^2 ))×(2/n)=(1/4) but now it gives (1/n) not (2/n) , so it needs to be multiplied by (1/2)](Q62606.png)
$${The}\:{definite}\:{integral}\:{of}\:{a}\:{continuous} \\ $$$${function}\:{f}\left({x}\right)\:{over}\:{the}\:{interval}\left[{a}\:,\:{b}\right] \\ $$$$,{denoted}\:{by}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx},\:{is}\:{the}\:{limit}\:{of}\: \\ $$$${Riemann}\:{sum}\:{as}\:{the}\:{number}\:{of} \\ $$$${subdivisions}\:{approaches}\:{infinity} \\ $$$${i}.{e}\:\int_{{a}} ^{{b}} {f}\left({x}\right){dx}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\bigtriangleup{xf}\left({x}_{{k}} \right) \\ $$$${where}\:\bigtriangleup{x}=\frac{{b}−{a}}{{n}}\:{and}\:{x}_{{k}} ={a}+{k}\bigtriangleup{x} \\ $$$${now}\:{we}\:{have}\:\bigtriangleup{x}=\frac{\mathrm{2}}{{n}}\:,\:{means}\:{the} \\ $$$${constant}\:{width}\:{of}\:{the}\:{rectangle}, \\ $$$${and}\:{x}_{{k}} \:{is}\:{the}\:{x}\:{value}\:{of}\:{the}\:{right}\: \\ $$$${edge}\:{of}\:{the}\:{k}^{{th}} \:{rectangle},{from} \\ $$$${x}_{\mathrm{1}} =\mathrm{2}+\frac{\mathrm{1}}{{n}}\:{to}\:{x}_{{n}} =\:\mathrm{4}−\frac{\mathrm{1}}{{n}}\:,{then}\:{f}\left({x}_{{k}} \right) \\ $$$${will}\:{give}\:{us}\:{the}\:{height}\:{of}\:\:{each} \\ $$$${rectangle}\:,{and}\:{here}\:{f}\left({x}\right)=\frac{\mathrm{1}}{{x}^{\mathrm{2}} }\:,\:{so}\:{the} \\ $$$${area}\:{of}\:{the}\:{k}^{{th}} \:{rectangle}\:{is} \\ $$$$\frac{\mathrm{2}}{{n}}×\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{2}}{{n}}{k}\right)^{\mathrm{2}} }\:,\:{and}\:{we}\:{sum}\:{that}\:{for} \\ $$$${values}\:{of}\:{k}\:{from}\:\mathrm{1}\:{to}\:{n} \\ $$$${R}\left({n}\right)=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{2}}{{n}}{k}\right)^{\mathrm{2}} }×\frac{\mathrm{2}}{{n}} \\ $$$${now}\:{we}\:{can}\:{represent}\:{the}\:{actual} \\ $$$${area}\:{as}\:{a}\:{limit}: \\ $$$$\int_{\mathrm{2}\:} ^{\mathrm{4}} \frac{\mathrm{1}}{{x}^{\mathrm{2}} }{dx}=\underset{{n}\rightarrow\infty} {\mathrm{lim}}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{\mathrm{1}}{\left(\mathrm{2}+\frac{\mathrm{2}}{{n}}{k}\right)^{\mathrm{2}} }×\frac{\mathrm{2}}{{n}}=\frac{\mathrm{1}}{\mathrm{4}} \\ $$$${but}\:{now}\:{it}\:{gives}\:\frac{\mathrm{1}}{{n}}\:{not}\:\frac{\mathrm{2}}{{n}}\:, \\ $$$${so}\:{it}\:{needs}\:{to}\:{be}\:{multiplied}\:{by}\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$
Commented by Joel122 last updated on 24/Jun/19
$${thank}\:{you}\:{very}\:{much} \\ $$
