
Previous in Relation and Functions Next in Relation and Functions
Question Number 132932 by bobhans last updated on 17/Feb/21
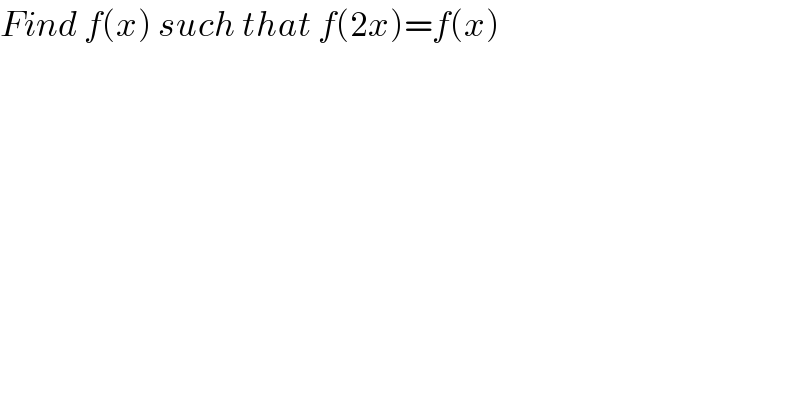
$${Find}\:{f}\left({x}\right)\:{such}\:{that}\:{f}\left(\mathrm{2}{x}\right)={f}\left({x}\right) \\ $$
Answered by Olaf last updated on 17/Feb/21
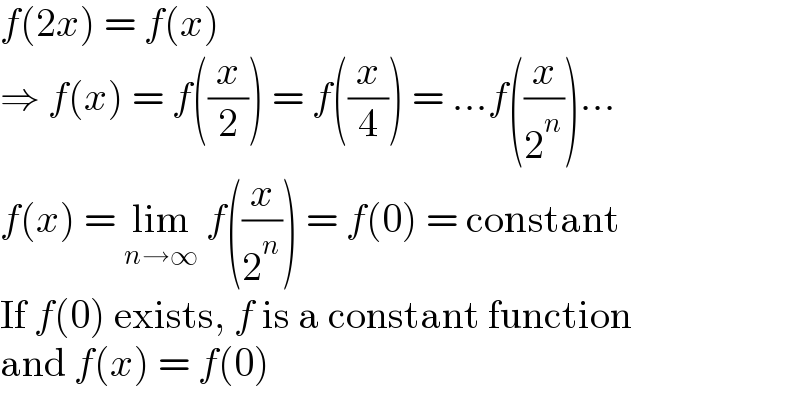
$${f}\left(\mathrm{2}{x}\right)\:=\:{f}\left({x}\right) \\ $$$$\Rightarrow\:{f}\left({x}\right)\:=\:{f}\left(\frac{{x}}{\mathrm{2}}\right)\:=\:{f}\left(\frac{{x}}{\mathrm{4}}\right)\:=\:...{f}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)... \\ $$$${f}\left({x}\right)\:=\:\underset{{n}\rightarrow\infty} {\mathrm{lim}}\:{f}\left(\frac{{x}}{\mathrm{2}^{{n}} }\right)\:=\:{f}\left(\mathrm{0}\right)\:=\:\mathrm{constant} \\ $$$$\mathrm{If}\:{f}\left(\mathrm{0}\right)\:\mathrm{exists},\:{f}\:\mathrm{is}\:\mathrm{a}\:\mathrm{constant}\:\mathrm{function} \\ $$$$\mathrm{and}\:{f}\left({x}\right)\:=\:{f}\left(\mathrm{0}\right) \\ $$
