
Question Number 29202 by ajfour last updated on 05/Feb/18
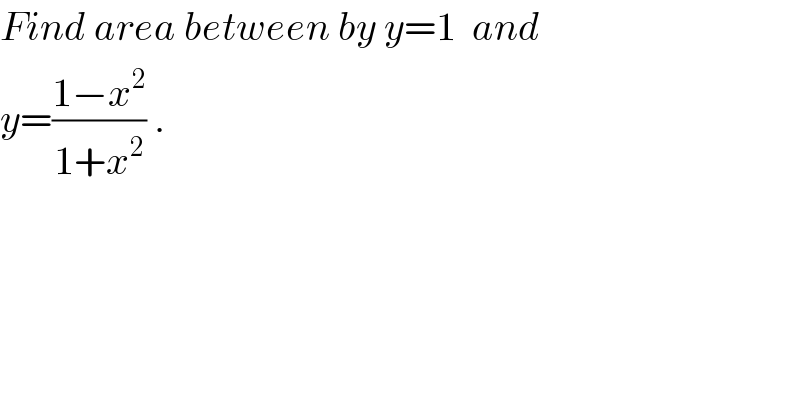
$${Find}\:{area}\:{between}\:{by}\:{y}=\mathrm{1}\:\:{and} \\ $$$${y}=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:. \\ $$
Answered by mrW2 last updated on 05/Feb/18
![y=((1−x^2 )/(1+x^2 ))=(2/(1+x^2 ))−1 if x→±∞, y→y_(min) =−1 if x=0, y=y_(max) =1 if x=±1, y=0 Area between y=−1 and y=((1−x^2 )/(1+x^2 )): A=2∫_0 ^(+∞) (y+1)dx =2∫_0 ^(+∞) ((2/(1+x^2 )))dx =4∫_0 ^(+∞) ((1/(1+x^2 )))dx =4[tan^(−1) x]_0 ^(+∞) =4((π/2)−0) =2π](Q29233.png)
$${y}=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }=\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }−\mathrm{1} \\ $$$${if}\:{x}\rightarrow\pm\infty,\:{y}\rightarrow{y}_{{min}} =−\mathrm{1} \\ $$$${if}\:{x}=\mathrm{0},\:{y}={y}_{{max}} =\mathrm{1} \\ $$$${if}\:{x}=\pm\mathrm{1},\:{y}=\mathrm{0} \\ $$$$ \\ $$$${Area}\:{between}\:{y}=−\mathrm{1}\:{and}\:{y}=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }: \\ $$$${A}=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \left({y}+\mathrm{1}\right){dx} \\ $$$$=\mathrm{2}\int_{\mathrm{0}} ^{+\infty} \left(\frac{\mathrm{2}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\mathrm{4}\int_{\mathrm{0}} ^{+\infty} \left(\frac{\mathrm{1}}{\mathrm{1}+{x}^{\mathrm{2}} }\right){dx} \\ $$$$=\mathrm{4}\left[\mathrm{tan}^{−\mathrm{1}} {x}\right]_{\mathrm{0}} ^{+\infty} \\ $$$$=\mathrm{4}\left(\frac{\pi}{\mathrm{2}}−\mathrm{0}\right) \\ $$$$=\mathrm{2}\pi \\ $$
Commented by mrW2 last updated on 05/Feb/18
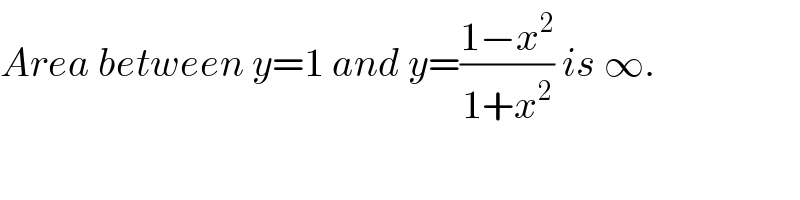
$${Area}\:{between}\:{y}=\mathrm{1}\:{and}\:{y}=\frac{\mathrm{1}−{x}^{\mathrm{2}} }{\mathrm{1}+{x}^{\mathrm{2}} }\:{is}\:\infty. \\ $$
Commented by ajfour last updated on 05/Feb/18
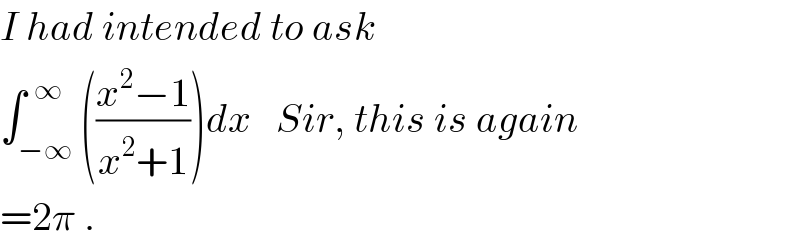
$${I}\:{had}\:{intended}\:{to}\:{ask} \\ $$$$\int_{−\infty} ^{\:\:\infty} \left(\frac{{x}^{\mathrm{2}} −\mathrm{1}}{{x}^{\mathrm{2}} +\mathrm{1}}\right){dx}\:\:\:{Sir},\:{this}\:{is}\:{again} \\ $$$$=\mathrm{2}\pi\:. \\ $$
Commented by mrW2 last updated on 05/Feb/18

$${I}\:{see}. \\ $$
