
Question Number 10856 by Joel576 last updated on 27/Feb/17
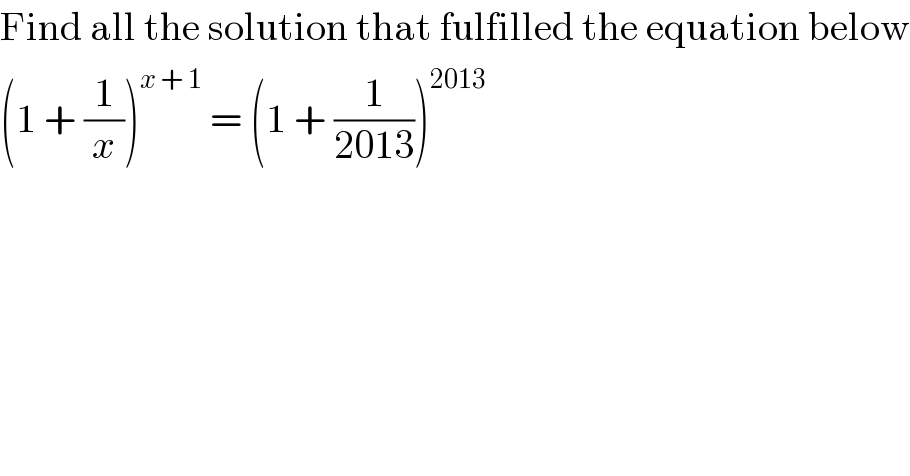
$$\mathrm{Find}\:\mathrm{all}\:\mathrm{the}\:\mathrm{solution}\:\mathrm{that}\:\mathrm{fulfilled}\:\mathrm{the}\:\mathrm{equation}\:\mathrm{below} \\ $$$$\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{{x}}\right)^{{x}\:+\:\mathrm{1}} \:=\:\left(\mathrm{1}\:+\:\frac{\mathrm{1}}{\mathrm{2013}}\right)^{\mathrm{2013}} \\ $$
Answered by DrDaveR last updated on 12/Mar/17
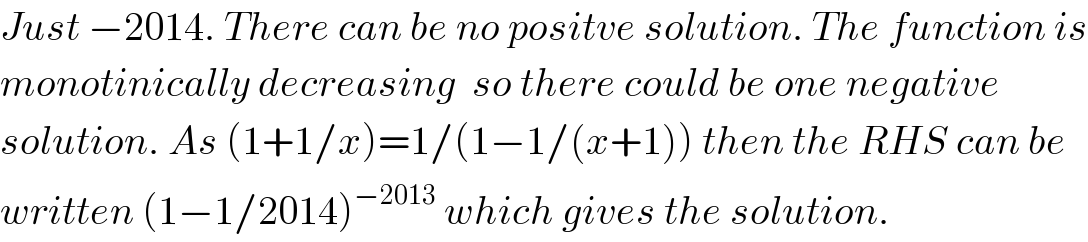
$${Just}\:−\mathrm{2014}.\:{There}\:{can}\:{be}\:{no}\:{positve}\:{solution}.\:{The}\:{function}\:{is} \\ $$$${monotinically}\:{decreasing}\:\:{so}\:{there}\:{could}\:{be}\:{one}\:{negative}\: \\ $$$${solution}.\:{As}\:\left(\mathrm{1}+\mathrm{1}/{x}\right)=\mathrm{1}/\left(\mathrm{1}−\mathrm{1}/\left({x}+\mathrm{1}\right)\right)\:{then}\:{the}\:{RHS}\:{can}\:{be} \\ $$$${written}\:\left(\mathrm{1}−\mathrm{1}/\mathrm{2014}\right)^{−\mathrm{2013}} \:{which}\:{gives}\:{the}\:{solution}. \\ $$
