Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 216995 by Rasheed.Sindhi last updated on 26/Feb/25

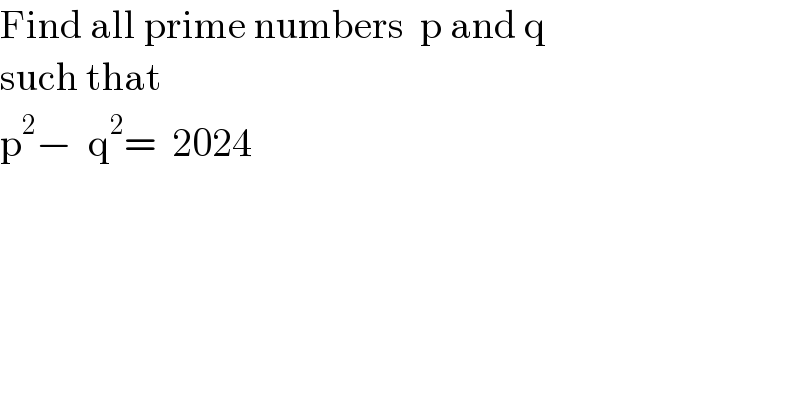
Find all prime numbers p and q such that p^2 − q^2 = 2024

$$\mathrm{Find}\:\mathrm{all}\:\mathrm{prime}\:\mathrm{numbers}\:\:\mathrm{p}\:\mathrm{and}\:\mathrm{q}\: \\ $$$$\mathrm{such}\:\mathrm{that} \\ $$$$\mathrm{p}^{\mathrm{2}} −\:\:\mathrm{q}^{\mathrm{2}} =\:\:\mathrm{2024} \\ $$

Answered by Marzuk last updated on 26/Feb/25

(p+q)(p−q)=2024 2024 = 2×1012 = 4×506 =8× 253 =88×23 =1×2024 =22×92 =11×184 =44×46 p+q+p−q=2p that means sum of the each pair has to be divisible by 2 2+1012=1014 4+506=510 8+253=261 88+23=111 1+2024=2025 22+92=114 11+184=195 44+46=90 so we have left 4 pairs 2×1012 4×506 22×92 44×46 lets see if the dividend is the sumof each pair and the divisor is 2 then the quotient is ∈ P ((Σ(2,1012))/2) ∉ P ((Σ(4,506))/2) ∉ P ((Σ(22,92))/2) ∉ P ((Σ(44,46))/2) ∉ P So,the set of all possible prime values of is ∅

$$ \\ $$$$\left({p}+{q}\right)\left({p}−{q}\right)=\mathrm{2024} \\ $$$$\mathrm{2024}\:=\:\mathrm{2}×\mathrm{1012} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\:\mathrm{4}×\mathrm{506} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{8}×\:\mathrm{253} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{88}×\mathrm{23} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{1}×\mathrm{2024} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{22}×\mathrm{92} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{11}×\mathrm{184} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:=\mathrm{44}×\mathrm{46} \\ $$$${p}+{q}+{p}−{q}=\mathrm{2}{p} \\ $$$${that}\:{means}\:{sum}\:{of}\:{the}\:{each}\:{pair}\:{has} \\ $$$${to}\:{be}\:{divisible}\:{by}\:\mathrm{2} \\ $$$$\mathrm{2}+\mathrm{1012}=\mathrm{1014} \\ $$$$\mathrm{4}+\mathrm{506}=\mathrm{510} \\ $$$$\mathrm{8}+\mathrm{253}=\mathrm{261} \\ $$$$\mathrm{88}+\mathrm{23}=\mathrm{111} \\ $$$$\mathrm{1}+\mathrm{2024}=\mathrm{2025} \\ $$$$\mathrm{22}+\mathrm{92}=\mathrm{114} \\ $$$$\mathrm{11}+\mathrm{184}=\mathrm{195} \\ $$$$\mathrm{44}+\mathrm{46}=\mathrm{90} \\ $$$${so}\:{we}\:{have}\:{left}\:\mathrm{4}\:{pairs} \\ $$$$\mathrm{2}×\mathrm{1012} \\ $$$$\mathrm{4}×\mathrm{506} \\ $$$$\mathrm{22}×\mathrm{92} \\ $$$$\mathrm{44}×\mathrm{46} \\ $$$${lets}\:{see}\:{if}\:{the}\:{dividend}\:{is}\:{the}\:{sumof}\:{each} \\ $$$${pair}\:{and}\:{the}\:{divisor}\:{is}\:\mathrm{2}\:{then}\:{the}\:{quotient} \\ $$$${is}\:\in\:\mathbb{P} \\ $$$$\frac{\Sigma\left(\mathrm{2},\mathrm{1012}\right)}{\mathrm{2}}\:\:\notin\:\mathbb{P} \\ $$$$\frac{\Sigma\left(\mathrm{4},\mathrm{506}\right)}{\mathrm{2}}\:\notin\:\mathbb{P} \\ $$$$\frac{\Sigma\left(\mathrm{22},\mathrm{92}\right)}{\mathrm{2}}\:\notin\:\mathbb{P} \\ $$$$\frac{\Sigma\left(\mathrm{44},\mathrm{46}\right)}{\mathrm{2}}\:\notin\:\mathbb{P}\: \\ $$$${So},{the}\:{set}\:{of}\:{all}\:{possible}\:{prime}\:{values}\:{of} \\ $$$${is}\:\emptyset\: \\ $$

Commented by Rasheed.Sindhi last updated on 26/Feb/25

Thanks sir!

$$\mathcal{T}{hanks}\:{sir}! \\ $$

Answered by mehdee7396 last updated on 26/Feb/25

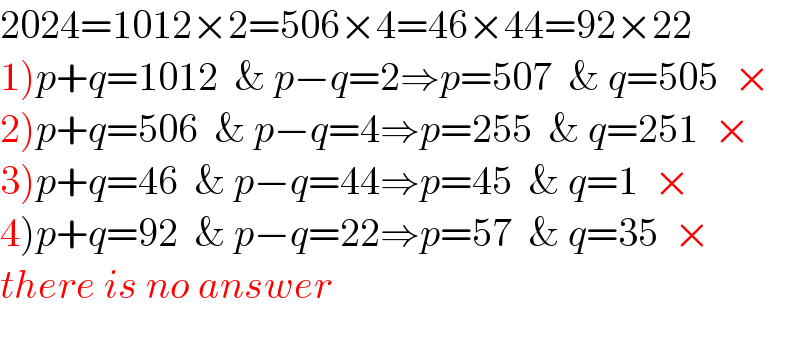
2024=1012×2=506×4=46×44=92×22 1)p+q=1012 & p−q=2⇒p=507 & q=505 × 2)p+q=506 & p−q=4⇒p=255 & q=251 × 3)p+q=46 & p−q=44⇒p=45 & q=1 × 4)p+q=92 & p−q=22⇒p=57 & q=35 × there is no answer

$$\mathrm{2024}=\mathrm{1012}×\mathrm{2}=\mathrm{506}×\mathrm{4}=\mathrm{46}×\mathrm{44}=\mathrm{92}×\mathrm{22} \\ $$$$\left.\mathrm{1}\right){p}+{q}=\mathrm{1012}\:\:\&\:{p}−{q}=\mathrm{2}\Rightarrow{p}=\mathrm{507}\:\:\&\:{q}=\mathrm{505}\:\:× \\ $$$$\left.\mathrm{2}\right){p}+{q}=\mathrm{506}\:\:\&\:{p}−{q}=\mathrm{4}\Rightarrow{p}=\mathrm{255}\:\:\&\:{q}=\mathrm{251}\:\:× \\ $$$$\left.\mathrm{3}\right){p}+{q}=\mathrm{46}\:\:\&\:{p}−{q}=\mathrm{44}\Rightarrow{p}=\mathrm{45}\:\:\&\:{q}=\mathrm{1}\:\:× \\ $$$$\left.\mathrm{4}\right){p}+{q}=\mathrm{92}\:\:\&\:{p}−{q}=\mathrm{22}\Rightarrow{p}=\mathrm{57}\:\:\&\:{q}=\mathrm{35}\:\:× \\ $$$${there}\:{is}\:{no}\:{answer} \\ $$$$\: \\ $$

Commented by Rasheed.Sindhi last updated on 26/Feb/25

Thanx sir!

$$\mathbb{T}\mathrm{hanx}\:\mathrm{sir}! \\ $$

Answered by MathematicalUser2357 last updated on 01/Mar/25

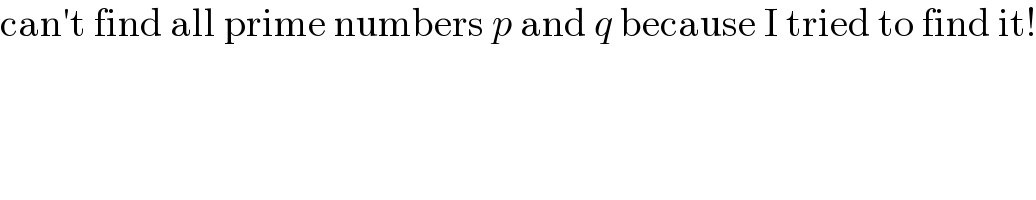
can′t find all prime numbers p and q because I tried to find it!

$$\mathrm{can}'\mathrm{t}\:\mathrm{find}\:\mathrm{all}\:\mathrm{prime}\:\mathrm{numbers}\:{p}\:\mathrm{and}\:{q}\:\mathrm{because}\:\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{find}\:\mathrm{it}! \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com