Question and Answers Forum

All Questions      Topic List

Matrices and Determinants Questions

Previous in All Question      Next in All Question      

Previous in Matrices and Determinants      Next in Matrices and Determinants      

Question Number 199847 by cortano12 last updated on 10/Nov/23

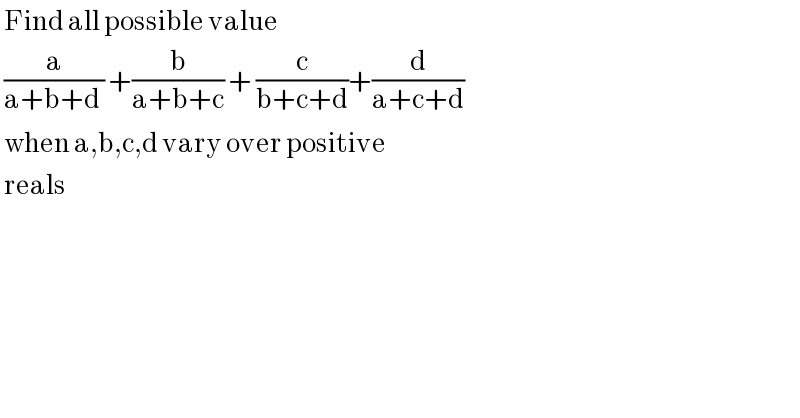
Find all possible value (a/(a+b+d )) +(b/(a+b+c)) + (c/(b+c+d))+(d/(a+c+d)) when a,b,c,d vary over positive reals

$$\:\mathrm{Find}\:\mathrm{all}\:\mathrm{possible}\:\mathrm{value}\: \\ $$$$\:\frac{\mathrm{a}}{\mathrm{a}+\mathrm{b}+\mathrm{d}\:}\:+\frac{\mathrm{b}}{\mathrm{a}+\mathrm{b}+\mathrm{c}}\:+\:\frac{\mathrm{c}}{\mathrm{b}+\mathrm{c}+\mathrm{d}}+\frac{\mathrm{d}}{\mathrm{a}+\mathrm{c}+\mathrm{d}}\: \\ $$$$\:\mathrm{when}\:\mathrm{a},\mathrm{b},\mathrm{c},\mathrm{d}\:\mathrm{vary}\:\mathrm{over}\:\mathrm{positive} \\ $$$$\:\mathrm{reals}\: \\ $$

Commented by Frix last updated on 10/Nov/23

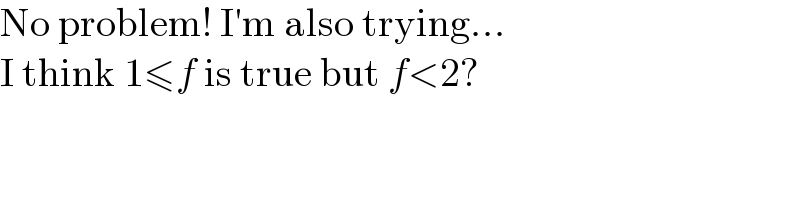
No problem! I′m also trying... I think 1≤f is true but f<2?

$$\mathrm{No}\:\mathrm{problem}!\:\mathrm{I}'\mathrm{m}\:\mathrm{also}\:\mathrm{trying}... \\ $$$$\mathrm{I}\:\mathrm{think}\:\mathrm{1}\leqslant{f}\:\mathrm{is}\:\mathrm{true}\:\mathrm{but}\:{f}<\mathrm{2}? \\ $$

Commented by witcher3 last updated on 10/Nov/23

i didnt want delate Y re coment

$$\mathrm{i}\:\mathrm{didnt}\:\mathrm{want}\:\mathrm{delate}\:\mathrm{Y}\:\mathrm{re}\:\mathrm{coment} \\ $$

Commented by witcher3 last updated on 10/Nov/23

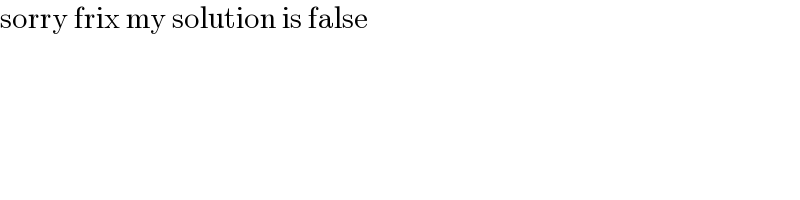
sorry frix my solution is false

$$\mathrm{sorry}\:\mathrm{frix}\:\mathrm{my}\:\mathrm{solution}\:\mathrm{is}\:\mathrm{false} \\ $$

Commented by witcher3 last updated on 12/Nov/23

f<2 i?think also

$$\mathrm{f}<\mathrm{2}\:\mathrm{i}?\mathrm{think}\:\mathrm{also} \\ $$

Commented by witcher3 last updated on 12/Nov/23

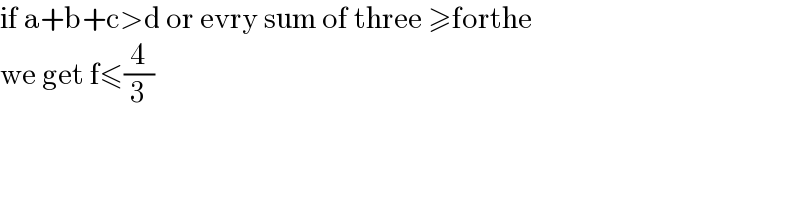
if a+b+c>d or evry sum of three ≥forthe we get f≤(4/3)

$$\mathrm{if}\:\mathrm{a}+\mathrm{b}+\mathrm{c}>\mathrm{d}\:\mathrm{or}\:\mathrm{evry}\:\mathrm{sum}\:\mathrm{of}\:\mathrm{three}\:\geqslant\mathrm{forthe} \\ $$$$\mathrm{we}\:\mathrm{get}\:\mathrm{f}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$$$ \\ $$

Commented by Frix last updated on 12/Nov/23

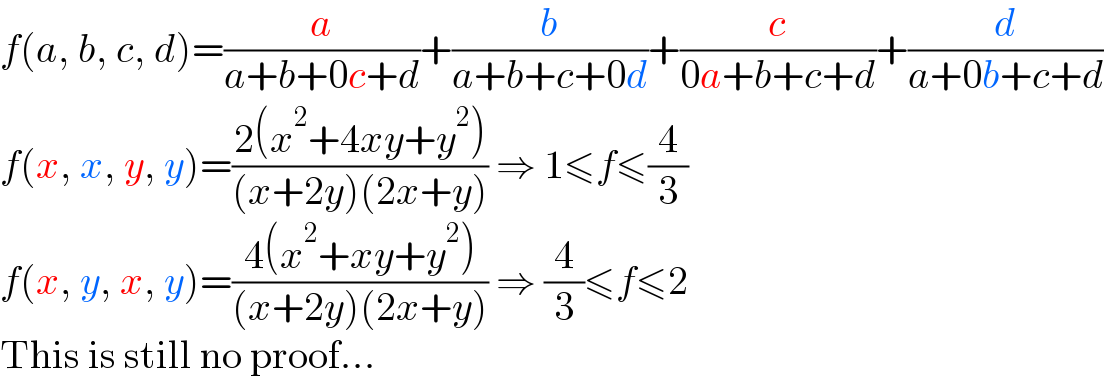
f(a, b, c, d)=(a/(a+b+0c+d))+(b/(a+b+c+0d))+(c/(0a+b+c+d))+(d/(a+0b+c+d)) f(x, x, y, y)=((2(x^2 +4xy+y^2 ))/((x+2y)(2x+y))) ⇒ 1≤f≤(4/3) f(x, y, x, y)=((4(x^2 +xy+y^2 ))/((x+2y)(2x+y))) ⇒ (4/3)≤f≤2 This is still no proof...

$${f}\left({a},\:{b},\:{c},\:{d}\right)=\frac{{a}}{{a}+{b}+\mathrm{0}{c}+{d}}+\frac{{b}}{{a}+{b}+{c}+\mathrm{0}{d}}+\frac{{c}}{\mathrm{0}{a}+{b}+{c}+{d}}+\frac{{d}}{{a}+\mathrm{0}{b}+{c}+{d}} \\ $$$${f}\left({x},\:{x},\:{y},\:{y}\right)=\frac{\mathrm{2}\left({x}^{\mathrm{2}} +\mathrm{4}{xy}+{y}^{\mathrm{2}} \right)}{\left({x}+\mathrm{2}{y}\right)\left(\mathrm{2}{x}+{y}\right)}\:\Rightarrow\:\mathrm{1}\leqslant{f}\leqslant\frac{\mathrm{4}}{\mathrm{3}} \\ $$$${f}\left({x},\:{y},\:{x},\:{y}\right)=\frac{\mathrm{4}\left({x}^{\mathrm{2}} +{xy}+{y}^{\mathrm{2}} \right)}{\left({x}+\mathrm{2}{y}\right)\left(\mathrm{2}{x}+{y}\right)}\:\Rightarrow\:\frac{\mathrm{4}}{\mathrm{3}}\leqslant{f}\leqslant\mathrm{2} \\ $$$$\mathrm{This}\:\mathrm{is}\:\mathrm{still}\:\mathrm{no}\:\mathrm{proof}... \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com