Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 216783 by ArshadS last updated on 20/Feb/25

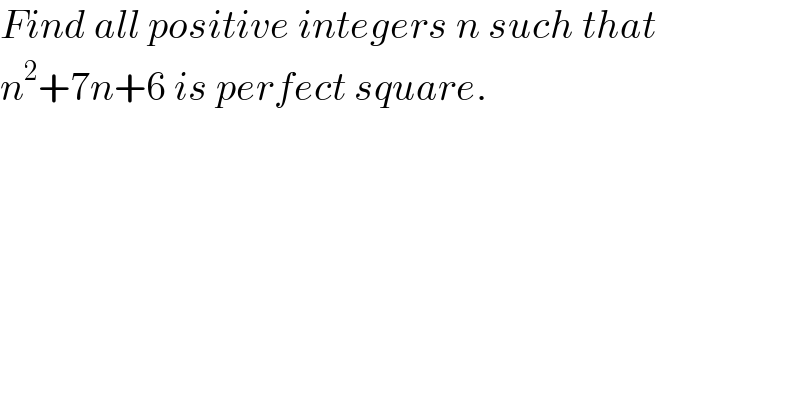
Find all positive integers n such that n^2 +7n+6 is perfect square.

$${Find}\:{all}\:{positive}\:{integers}\:{n}\:{such}\:{that} \\ $$$${n}^{\mathrm{2}} +\mathrm{7}{n}+\mathrm{6}\:{is}\:{perfect}\:{square}. \\ $$

Answered by mehdee7396 last updated on 20/Feb/25

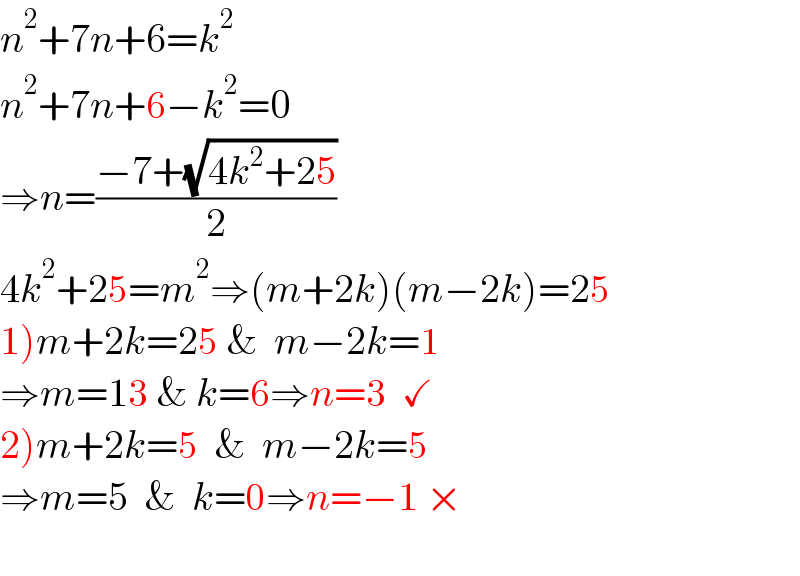
n^2 +7n+6=k^2 n^2 +7n+6−k^2 =0 ⇒n=((−7+(√(4k^2 +25)))/2) 4k^2 +25=m^2 ⇒(m+2k)(m−2k)=25 1)m+2k=25 & m−2k=1 ⇒m=13 & k=6⇒n=3 ✓ 2)m+2k=5 & m−2k=5 ⇒m=5 & k=0⇒n=−1 ×

$${n}^{\mathrm{2}} +\mathrm{7}{n}+\mathrm{6}={k}^{\mathrm{2}} \\ $$$${n}^{\mathrm{2}} +\mathrm{7}{n}+\mathrm{6}−{k}^{\mathrm{2}} =\mathrm{0} \\ $$$$\Rightarrow{n}=\frac{−\mathrm{7}+\sqrt{\mathrm{4}{k}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{2}} \\ $$$$\mathrm{4}{k}^{\mathrm{2}} +\mathrm{25}={m}^{\mathrm{2}} \Rightarrow\left({m}+\mathrm{2}{k}\right)\left({m}−\mathrm{2}{k}\right)=\mathrm{25} \\ $$$$\left.\mathrm{1}\right){m}+\mathrm{2}{k}=\mathrm{25}\:\&\:\:{m}−\mathrm{2}{k}=\mathrm{1} \\ $$$$\Rightarrow{m}=\mathrm{13}\:\&\:{k}=\mathrm{6}\Rightarrow{n}=\mathrm{3}\:\:\checkmark \\ $$$$\left.\mathrm{2}\right){m}+\mathrm{2}{k}=\mathrm{5}\:\:\&\:\:{m}−\mathrm{2}{k}=\mathrm{5} \\ $$$$\Rightarrow{m}=\mathrm{5}\:\:\&\:\:{k}=\mathrm{0}\Rightarrow{n}=−\mathrm{1}\:× \\ $$$$ \\ $$

Commented by ArshadS last updated on 21/Feb/25

Thanks sir!

$$\mathbb{T}\mathrm{hanks}\:\mathrm{sir}! \\ $$

Answered by Hanuda354 last updated on 21/Feb/25

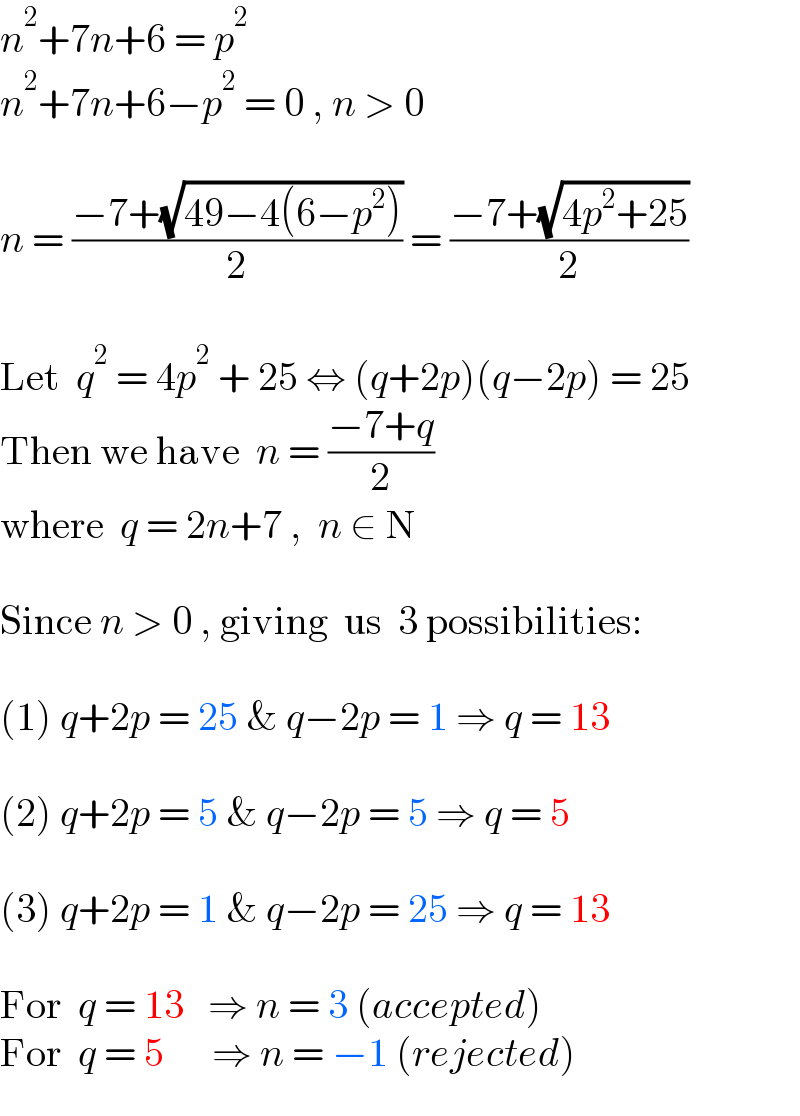
n^2 +7n+6 = p^2 n^2 +7n+6−p^2 = 0 , n > 0 n = ((−7+(√(49−4(6−p^2 ))))/2) = ((−7+(√(4p^2 +25)))/2) Let q^2 = 4p^2 + 25 ⇔ (q+2p)(q−2p) = 25 Then we have n = ((−7+q)/2) where q = 2n+7 , n ∈ N Since n > 0 , giving us 3 possibilities: (1) q+2p = 25 & q−2p = 1 ⇒ q = 13 (2) q+2p = 5 & q−2p = 5 ⇒ q = 5 (3) q+2p = 1 & q−2p = 25 ⇒ q = 13 For q = 13 ⇒ n = 3 (accepted) For q = 5 ⇒ n = −1 (rejected)

$${n}^{\mathrm{2}} +\mathrm{7}{n}+\mathrm{6}\:=\:{p}^{\mathrm{2}} \\ $$$${n}^{\mathrm{2}} +\mathrm{7}{n}+\mathrm{6}−{p}^{\mathrm{2}} \:=\:\mathrm{0}\:,\:{n}\:>\:\mathrm{0} \\ $$$$ \\ $$$${n}\:=\:\frac{−\mathrm{7}+\sqrt{\mathrm{49}−\mathrm{4}\left(\mathrm{6}−{p}^{\mathrm{2}} \right)}}{\mathrm{2}}\:=\:\frac{−\mathrm{7}+\sqrt{\mathrm{4}{p}^{\mathrm{2}} +\mathrm{25}}}{\mathrm{2}} \\ $$$$ \\ $$$$\mathrm{Let}\:\:{q}^{\mathrm{2}} \:=\:\mathrm{4}{p}^{\mathrm{2}} \:+\:\mathrm{25}\:\Leftrightarrow\:\left({q}+\mathrm{2}{p}\right)\left({q}−\mathrm{2}{p}\right)\:=\:\mathrm{25} \\ $$$$\mathrm{Then}\:\mathrm{we}\:\mathrm{have}\:\:{n}\:=\:\frac{−\mathrm{7}+{q}}{\mathrm{2}} \\ $$$$\mathrm{where}\:\:{q}\:=\:\mathrm{2}{n}+\mathrm{7}\:,\:\:{n}\:\in\:\mathrm{N} \\ $$$$ \\ $$$$\mathrm{Since}\:{n}\:>\:\mathrm{0}\:,\:\mathrm{giving}\:\:\mathrm{us}\:\:\mathrm{3}\:\mathrm{possibilities}: \\ $$$$ \\ $$$$\left(\mathrm{1}\right)\:{q}+\mathrm{2}{p}\:=\:\mathrm{25}\:\&\:{q}−\mathrm{2}{p}\:=\:\mathrm{1}\:\Rightarrow\:{q}\:=\:\mathrm{13} \\ $$$$ \\ $$$$\left(\mathrm{2}\right)\:{q}+\mathrm{2}{p}\:=\:\mathrm{5}\:\&\:{q}−\mathrm{2}{p}\:=\:\mathrm{5}\:\Rightarrow\:{q}\:=\:\mathrm{5} \\ $$$$ \\ $$$$\left(\mathrm{3}\right)\:{q}+\mathrm{2}{p}\:=\:\mathrm{1}\:\&\:{q}−\mathrm{2}{p}\:=\:\mathrm{25}\:\Rightarrow\:{q}\:=\:\mathrm{13} \\ $$$$ \\ $$$$\mathrm{For}\:\:{q}\:=\:\mathrm{13}\:\:\:\Rightarrow\:{n}\:=\:\mathrm{3}\:\left({accepted}\right) \\ $$$$\mathrm{For}\:\:{q}\:=\:\mathrm{5}\:\:\:\:\:\:\Rightarrow\:{n}\:=\:−\mathrm{1}\:\left({rejected}\right) \\ $$

Commented by ArshadS last updated on 21/Feb/25

Thanks sir!

$$\mathcal{T}{hanks}\:{sir}! \\ $$

Answered by Rasheed.Sindhi last updated on 21/Feb/25

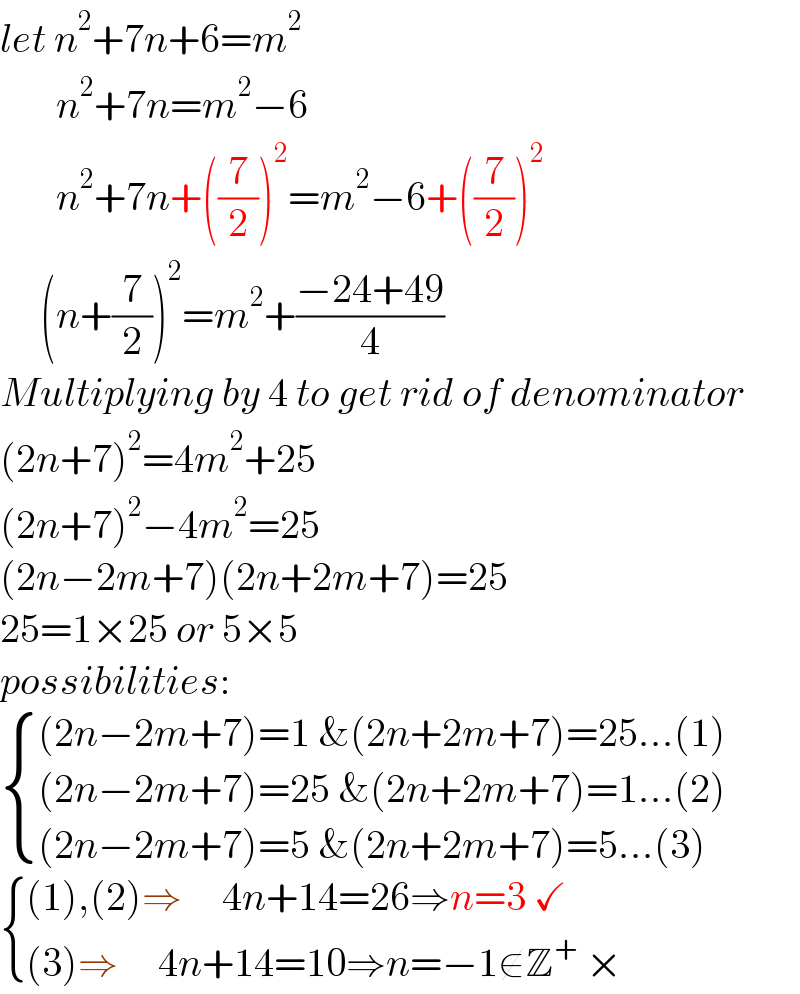
let n^2 +7n+6=m^2 n^2 +7n=m^2 −6 n^2 +7n+((7/2))^2 =m^2 −6+((7/2))^2 (n+(7/2))^2 =m^2 +((−24+49)/4) Multiplying by 4 to get rid of denominator (2n+7)^2 =4m^2 +25 (2n+7)^2 −4m^2 =25 (2n−2m+7)(2n+2m+7)=25 25=1×25 or 5×5 possibilities: { (((2n−2m+7)=1 &(2n+2m+7)=25...(1))),(((2n−2m+7)=25 &(2n+2m+7)=1...(2))),(((2n−2m+7)=5 &(2n+2m+7)=5...(3))) :} { (((1),(2)⇒ 4n+14=26⇒n=3 ✓)),(((3)⇒ 4n+14=10⇒n=−1∉Z^+ ×)) :}

$${let}\:{n}^{\mathrm{2}} +\mathrm{7}{n}+\mathrm{6}={m}^{\mathrm{2}} \\ $$$$\:\:\:\:\:\:\:{n}^{\mathrm{2}} +\mathrm{7}{n}={m}^{\mathrm{2}} −\mathrm{6} \\ $$$$\:\:\:\:\:\:\:{n}^{\mathrm{2}} +\mathrm{7}{n}+\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} ={m}^{\mathrm{2}} −\mathrm{6}+\left(\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} \\ $$$$\:\:\:\:\:\left({n}+\frac{\mathrm{7}}{\mathrm{2}}\right)^{\mathrm{2}} ={m}^{\mathrm{2}} +\frac{−\mathrm{24}+\mathrm{49}}{\mathrm{4}} \\ $$$${Multiplying}\:{by}\:\mathrm{4}\:{to}\:{get}\:{rid}\:{of}\:{denominator} \\ $$$$\left(\mathrm{2}{n}+\mathrm{7}\right)^{\mathrm{2}} =\mathrm{4}{m}^{\mathrm{2}} +\mathrm{25} \\ $$$$\left(\mathrm{2}{n}+\mathrm{7}\right)^{\mathrm{2}} −\mathrm{4}{m}^{\mathrm{2}} =\mathrm{25} \\ $$$$\left(\mathrm{2}{n}−\mathrm{2}{m}+\mathrm{7}\right)\left(\mathrm{2}{n}+\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{25} \\ $$$$\mathrm{25}=\mathrm{1}×\mathrm{25}\:{or}\:\mathrm{5}×\mathrm{5} \\ $$$${possibilities}: \\ $$$$\begin{cases}{\left(\mathrm{2}{n}−\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{1}\:\&\left(\mathrm{2}{n}+\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{25}...\left(\mathrm{1}\right)}\\{\left(\mathrm{2}{n}−\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{25}\:\&\left(\mathrm{2}{n}+\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{1}...\left(\mathrm{2}\right)}\\{\left(\mathrm{2}{n}−\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{5}\:\&\left(\mathrm{2}{n}+\mathrm{2}{m}+\mathrm{7}\right)=\mathrm{5}...\left(\mathrm{3}\right)}\end{cases} \\ $$$$\begin{cases}{\left(\mathrm{1}\right),\left(\mathrm{2}\right)\Rightarrow\:\:\:\:\:\mathrm{4}{n}+\mathrm{14}=\mathrm{26}\Rightarrow{n}=\mathrm{3}\:\checkmark}\\{\left(\mathrm{3}\right)\Rightarrow\:\:\:\:\:\mathrm{4}{n}+\mathrm{14}=\mathrm{10}\Rightarrow{n}=−\mathrm{1}\notin\mathbb{Z}^{+} \:×}\end{cases} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com