
Question Number 153012 by bobhans last updated on 04/Sep/21
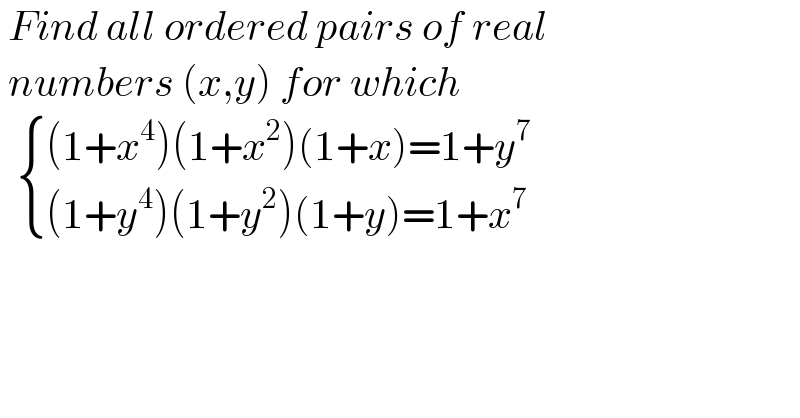
$$\:{Find}\:{all}\:{ordered}\:{pairs}\:{of}\:{real}\: \\ $$$$\:{numbers}\:\left({x},{y}\right)\:{for}\:{which} \\ $$$$\:\:\begin{cases}{\left(\mathrm{1}+{x}^{\mathrm{4}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}\right)=\mathrm{1}+{y}^{\mathrm{7}} }\\{\left(\mathrm{1}+{y}^{\mathrm{4}} \right)\left(\mathrm{1}+{y}^{\mathrm{2}} \right)\left(\mathrm{1}+{y}\right)=\mathrm{1}+{x}^{\mathrm{7}} }\end{cases} \\ $$
Commented by mr W last updated on 04/Sep/21
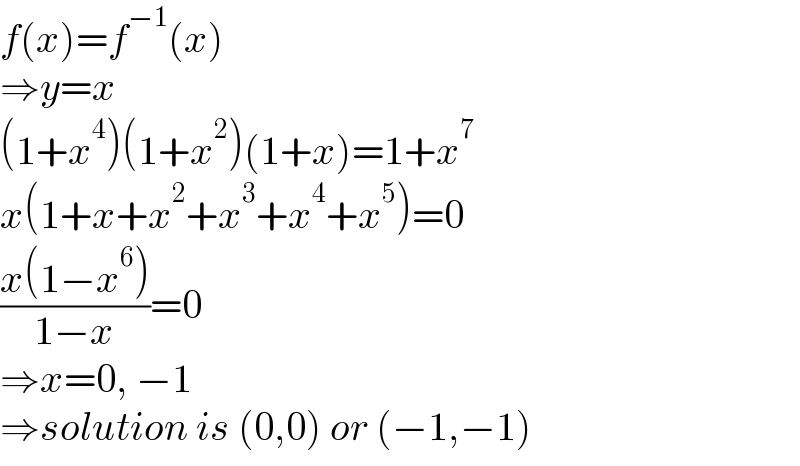
$${f}\left({x}\right)={f}^{−\mathrm{1}} \left({x}\right) \\ $$$$\Rightarrow{y}={x} \\ $$$$\left(\mathrm{1}+{x}^{\mathrm{4}} \right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)\left(\mathrm{1}+{x}\right)=\mathrm{1}+{x}^{\mathrm{7}} \\ $$$${x}\left(\mathrm{1}+{x}+{x}^{\mathrm{2}} +{x}^{\mathrm{3}} +{x}^{\mathrm{4}} +{x}^{\mathrm{5}} \right)=\mathrm{0} \\ $$$$\frac{{x}\left(\mathrm{1}−{x}^{\mathrm{6}} \right)}{\mathrm{1}−{x}}=\mathrm{0} \\ $$$$\Rightarrow{x}=\mathrm{0},\:−\mathrm{1} \\ $$$$\Rightarrow{solution}\:{is}\:\left(\mathrm{0},\mathrm{0}\right)\:{or}\:\left(−\mathrm{1},−\mathrm{1}\right) \\ $$
