Question and Answers Forum

All Questions      Topic List

Number Theory Questions

Previous in All Question      Next in All Question      

Previous in Number Theory      Next in Number Theory      

Question Number 196672 by Rasheed.Sindhi last updated on 29/Aug/23

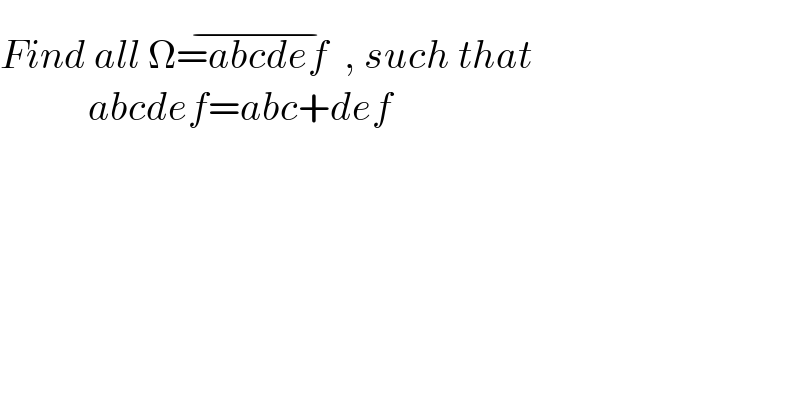
Find all Ω=abcdef ^(−) , such that abcdef=abc+def

$${Find}\:{all}\:\Omega\overline {={abcdef}\:\:},\:{such}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:{abcdef}={abc}+{def} \\ $$

Commented by Rasheed.Sindhi last updated on 29/Aug/23

Q#196659

$${Q}#\mathrm{196659} \\ $$

Answered by Rasheed.Sindhi last updated on 30/Aug/23

abcdef=abc+def abcdef−abc=def abc(def−1)=def abc=((def)/(def−1)) ⇒ (def−1)∣ def⇒def−1=1 ⇒def=2 { ((d=2,e=1,f=1)),((d=1,e=2,f=1)),((d=1,e=1,f=2)) :} def=211,121,112 abc=((def)/(def−1))=(2/1)=2 abc=211,121,112 Ω=abcdef^(−) =211211,211121,211112, 121211,121121,121112, 112211,112121,112112

$${abcdef}={abc}+{def} \\ $$$${abcdef}−{abc}={def} \\ $$$${abc}\left({def}−\mathrm{1}\right)={def} \\ $$$${abc}=\frac{{def}}{{def}−\mathrm{1}}\:\:\:\:\Rightarrow\:\left({def}−\mathrm{1}\right)\mid\:{def}\Rightarrow{def}−\mathrm{1}=\mathrm{1} \\ $$$$\Rightarrow{def}=\mathrm{2} \\ $$$$\begin{cases}{{d}=\mathrm{2},{e}=\mathrm{1},{f}=\mathrm{1}}\\{{d}=\mathrm{1},{e}=\mathrm{2},{f}=\mathrm{1}}\\{{d}=\mathrm{1},{e}=\mathrm{1},{f}=\mathrm{2}}\end{cases} \\ $$$${def}=\mathrm{211},\mathrm{121},\mathrm{112} \\ $$$${abc}=\frac{{def}}{{def}−\mathrm{1}}=\frac{\mathrm{2}}{\mathrm{1}}=\mathrm{2} \\ $$$${abc}=\mathrm{211},\mathrm{121},\mathrm{112} \\ $$$$\Omega=\overline {{abcdef}} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:=\mathrm{211211},\mathrm{211121},\mathrm{211112}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{121211},\mathrm{121121},\mathrm{121112}, \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathrm{112211},\mathrm{112121},\mathrm{112112} \\ $$

Commented by Tawa11 last updated on 29/Aug/23

Long time sir.

$$\mathrm{Long}\:\mathrm{time}\:\mathrm{sir}. \\ $$

Commented by Rasheed.Sindhi last updated on 30/Aug/23

Yes miss, nowadays I rarely can share any posts and you also less participate! Anyway thanks miss.

$${Yes}\:{miss},\:{nowadays}\:{I}\:{rarely}\:{can} \\ $$$$\:{share}\:{any}\:{posts}\:{and}\:{you}\:{also}\:{less} \\ $$$$\:{participate}! \\ $$$${Anyway}\:{thanks}\:{miss}. \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com