Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 206066 by hardmath last updated on 06/Apr/24

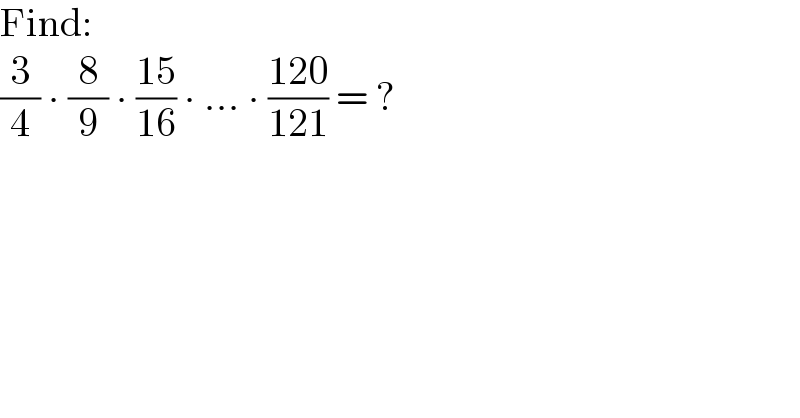
Find: (3/4) ∙ (8/9) ∙ ((15)/(16)) ∙ ... ∙ ((120)/(121)) = ?

$$\mathrm{Find}: \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\:\centerdot\:\frac{\mathrm{8}}{\mathrm{9}}\:\centerdot\:\frac{\mathrm{15}}{\mathrm{16}}\:\centerdot\:...\:\centerdot\:\frac{\mathrm{120}}{\mathrm{121}}\:=\:? \\ $$

Answered by mr W last updated on 06/Apr/24

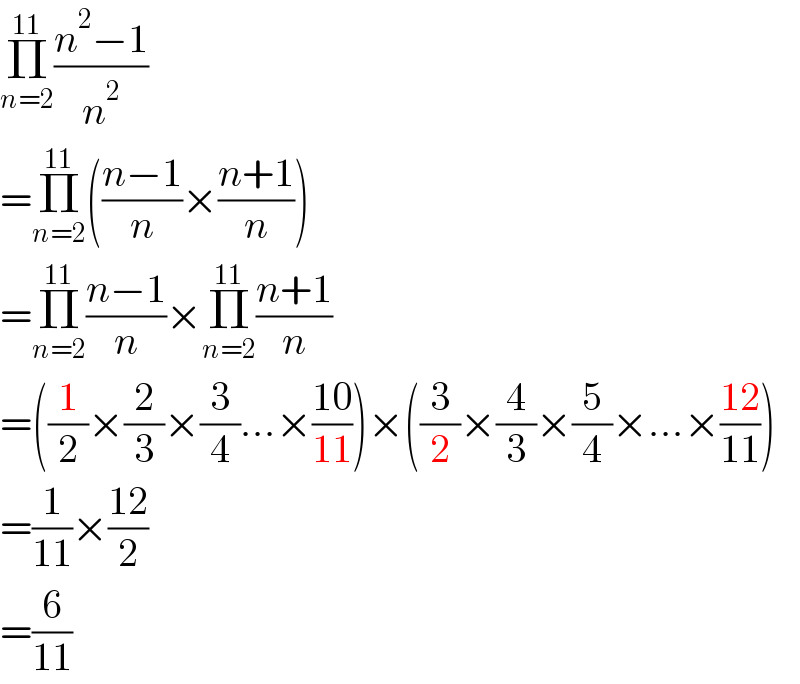
Π_(n=2) ^(11) ((n^2 −1)/n^2 ) =Π_(n=2) ^(11) (((n−1)/n)×((n+1)/n)) =Π_(n=2) ^(11) ((n−1)/n)×Π_(n=2) ^(11) ((n+1)/n) =((1/2)×(2/3)×(3/4)...×((10)/(11)))×((3/2)×(4/3)×(5/4)×...×((12)/(11))) =(1/(11))×((12)/2) =(6/(11))

$$\underset{{n}=\mathrm{2}} {\overset{\mathrm{11}} {\prod}}\frac{{n}^{\mathrm{2}} −\mathrm{1}}{{n}^{\mathrm{2}} } \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{\mathrm{11}} {\prod}}\left(\frac{{n}−\mathrm{1}}{{n}}×\frac{{n}+\mathrm{1}}{{n}}\right) \\ $$$$=\underset{{n}=\mathrm{2}} {\overset{\mathrm{11}} {\prod}}\frac{{n}−\mathrm{1}}{{n}}×\underset{{n}=\mathrm{2}} {\overset{\mathrm{11}} {\prod}}\frac{{n}+\mathrm{1}}{{n}} \\ $$$$=\left(\frac{\mathrm{1}}{\mathrm{2}}×\frac{\mathrm{2}}{\mathrm{3}}×\frac{\mathrm{3}}{\mathrm{4}}...×\frac{\mathrm{10}}{\mathrm{11}}\right)×\left(\frac{\mathrm{3}}{\mathrm{2}}×\frac{\mathrm{4}}{\mathrm{3}}×\frac{\mathrm{5}}{\mathrm{4}}×...×\frac{\mathrm{12}}{\mathrm{11}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{11}}×\frac{\mathrm{12}}{\mathrm{2}} \\ $$$$=\frac{\mathrm{6}}{\mathrm{11}} \\ $$

Commented by hardmath last updated on 06/Apr/24

cool dear professor thankyou

$$\mathrm{cool}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{thankyou} \\ $$

Answered by MATHEMATICSAM last updated on 06/Apr/24

We can see that each term in terms of n is ((n^2 − 1)/n^2 ) where n = 2, 3,4, ... , 11 respectively. ((n^2 − 1)/n^2 ) = (((n + 1)(n − 1))/(n.n)) (3/4) × (8/9) × ((15)/(16)) × ... × ((120)/(121)) = ((3 × 1)/(2 × 2)) × ((4 × 2)/(3 × 3)) × ((5 × 3)/(4 × 4)) × ... × ((12 × 10)/(11 × 11)) = (1/2) × ((12)/(11)) = (6/(11)) (Ans)

$$\mathrm{We}\:\mathrm{can}\:\mathrm{see}\:\mathrm{that}\:\mathrm{each}\:\mathrm{term}\:\mathrm{in}\:\mathrm{terms}\:\mathrm{of} \\ $$$${n}\:\mathrm{is}\:\frac{{n}^{\mathrm{2}} \:−\:\mathrm{1}}{{n}^{\mathrm{2}} }\:\mathrm{where}\:{n}\:=\:\mathrm{2},\:\mathrm{3},\mathrm{4},\:...\:,\:\mathrm{11}\: \\ $$$$\mathrm{respectively}. \\ $$$$\frac{{n}^{\mathrm{2}} \:−\:\mathrm{1}}{{n}^{\mathrm{2}} }\:=\:\frac{\left({n}\:+\:\mathrm{1}\right)\left({n}\:−\:\mathrm{1}\right)}{{n}.{n}}\: \\ $$$$ \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\:×\:\frac{\mathrm{8}}{\mathrm{9}}\:×\:\frac{\mathrm{15}}{\mathrm{16}}\:×\:...\:×\:\frac{\mathrm{120}}{\mathrm{121}} \\ $$$$=\:\frac{\cancel{\mathrm{3}}\:×\:\mathrm{1}}{\mathrm{2}\:×\:\cancel{\mathrm{2}}}\:×\:\frac{\cancel{\mathrm{4}}\:×\:\cancel{\mathrm{2}}}{\cancel{\mathrm{3}}\:×\:\cancel{\mathrm{3}}}\:×\:\frac{\cancel{\mathrm{5}}\:×\:\cancel{\mathrm{3}}}{\cancel{\mathrm{4}}\:×\:\cancel{\mathrm{4}}}\:×\:...\:×\:\frac{\mathrm{12}\:×\:\cancel{\mathrm{10}}}{\cancel{\mathrm{11}}\:×\:\mathrm{11}} \\ $$$$=\:\frac{\mathrm{1}}{\mathrm{2}}\:×\:\frac{\mathrm{12}}{\mathrm{11}}\:=\:\frac{\mathrm{6}}{\mathrm{11}}\:\left(\mathrm{Ans}\right)\:\: \\ $$

Commented by hardmath last updated on 06/Apr/24

thank you dear professor cool

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor}\:\mathrm{cool} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com