Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 216836 by hardmath last updated on 22/Feb/25

Find: (((1 + tan1°)(1 + tan2°)...(1 + tan44°))/((1−tan46°)(1−tan47°)...(1−tan89°))) = ?

$$\mathrm{Find}: \\ $$$$\frac{\left(\mathrm{1}\:+\:\mathrm{tan1}°\right)\left(\mathrm{1}\:+\:\mathrm{tan2}°\right)...\left(\mathrm{1}\:+\:\mathrm{tan44}°\right)}{\left(\mathrm{1}−\mathrm{tan46}°\right)\left(\mathrm{1}−\mathrm{tan47}°\right)...\left(\mathrm{1}−\mathrm{tan89}°\right)}\:=\:? \\ $$

Answered by BaliramKumar last updated on 22/Feb/25

1

$$\mathrm{1} \\ $$

Answered by mehdee7396 last updated on 22/Feb/25

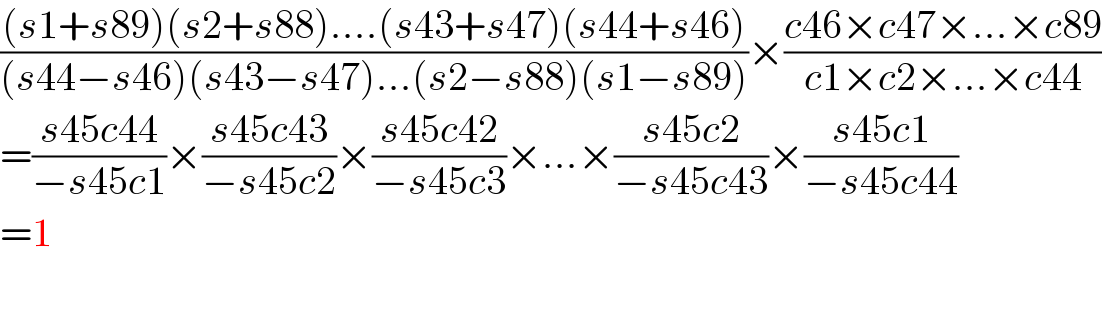
(((s1+s89)(s2+s88)....(s43+s47)(s44+s46))/((s44−s46)(s43−s47)...(s2−s88)(s1−s89)))×((c46×c47×...×c89)/(c1×c2×...×c44)) =((s45c44)/(−s45c1))×((s45c43)/(−s45c2))×((s45c42)/(−s45c3))×...×((s45c2)/(−s45c43))×((s45c1)/(−s45c44)) =1

$$\frac{\left({s}\mathrm{1}+{s}\mathrm{89}\right)\left({s}\mathrm{2}+{s}\mathrm{88}\right)....\left({s}\mathrm{43}+{s}\mathrm{47}\right)\left({s}\mathrm{44}+{s}\mathrm{46}\right)}{\left({s}\mathrm{44}−{s}\mathrm{46}\right)\left({s}\mathrm{43}−{s}\mathrm{47}\right)...\left({s}\mathrm{2}−{s}\mathrm{88}\right)\left({s}\mathrm{1}−{s}\mathrm{89}\right)}×\frac{{c}\mathrm{46}×{c}\mathrm{47}×...×{c}\mathrm{89}}{{c}\mathrm{1}×{c}\mathrm{2}×...×{c}\mathrm{44}} \\ $$$$=\frac{{s}\mathrm{45}{c}\mathrm{44}}{−{s}\mathrm{45}{c}\mathrm{1}}×\frac{{s}\mathrm{45}{c}\mathrm{43}}{−{s}\mathrm{45}{c}\mathrm{2}}×\frac{{s}\mathrm{45}{c}\mathrm{42}}{−{s}\mathrm{45}{c}\mathrm{3}}×...×\frac{{s}\mathrm{45}{c}\mathrm{2}}{−{s}\mathrm{45}{c}\mathrm{43}}×\frac{{s}\mathrm{45}{c}\mathrm{1}}{−{s}\mathrm{45}{c}\mathrm{44}} \\ $$$$=\mathrm{1}\:\: \\ $$$$ \\ $$

Commented by hardmath last updated on 22/Feb/25

s=sinus c=cosinus

$$\mathrm{s}=\mathrm{sinus} \\ $$$$\mathrm{c}=\mathrm{cosinus} \\ $$

Answered by MrGaster last updated on 23/Feb/25

Let P=Π_(k=1) ^(44) (1+tan k°)∧Q=Π_(k=46) ^(89) (1−tan k°).Find((P/Q)) tan(90°−x°)=cot x°⊢tan(90^° −x°)=cot x°,we have: tan(90°−k°)=cot k°=(1/(tan k°)) ⇒1−tan(90°−k)=1−(1/(tan k°))=((tan k°−1)/(tan k°)) Now consider the product: P∙Π_(k=1) ^(44) ((tan k°−1)/(tan k°))=Π_(k=1) ^(44) (1+tan k°)∙((tan k°−1)/(tan k°))=Π_(k=1) ^(44) (((tan k°+1)(tan k°−1))/(tan k°)) =Π_(k=1) ^(44) ((tan^2 k°−1)/(tan k°)) tan(45°+x°)=((1+tan x°)/(1−tanx°)) ⊢tan(45^° +k°)∙tan(45°−k°)=1 ⇒tan(45°+k°)=(1/(tan(45°−k°))) This implies: tan(45°+k°)∙tan(45∙k°)=((1+tan k°)/(1−tan k))∙((1−tan k)/(1+tan k))=1 so,Π simplifies to: P∙Π_(k=1) ^(44) ((tan k°−1)/(tan k°))=Π_(k=1) ^(44) ((tan^2 k°−1)/(tan k°))=Π_(k=1) ^(44) tan(45^° +k°)∙tan(45°−k°) =Π_(k=1) ^(44) 1=1 so,P=Π_(k=1) ^(44) ((tan k°)/(tan k°−1)),Now consider: (P/Q)=((Π_(k=1) ^(44) (1+tan k°))/(Π_(k=46) ^(89) (1−tan k°)))=Π_(k=1) ^(44) ((1+tan k°)/(1−tan(90°−k°))) =Π_(k=1) ^(44) ((1+tan k°)/(1−cot k°))=Π_(k=1) ^(44) ((1+tan k°)/((1−tan k°)/(tan k°))) =Π_(k=1) ^(44) ((tan k°(1+tan k°))/(1−tan k°)) tan(45°+x°)=((1+tan x°)/(1−tan x°)) ⊢tan(45°+k^° )=((1+tan k°)/(1−tan k°)) ⇒(P/Q)=Π_(k=1) ^(44) tan(45°+k°)=tan(45°+1°)∙tan(45+°2)∙…∙tan(45°+44°) ∵tan(45°+x°)=((1+tan x°)/(1−tan x))⇒(P/Q)=((1+tan 1)/(1−tan 1°))∙((1+tan 2°)/(1−tan 2°))∙…∙((1+tan 44°)/(1−tan 44°)) so,= determinant ((1))

$$\mathrm{Let}\:{P}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\left(\mathrm{1}+\mathrm{tan}\:{k}°\right)\wedge{Q}=\underset{{k}=\mathrm{46}} {\overset{\mathrm{89}} {\prod}}\left(\mathrm{1}−\mathrm{tan}\:{k}°\right).\mathrm{Find}\left(\frac{{P}}{{Q}}\right) \\ $$$$\mathrm{tan}\left(\mathrm{90}°−{x}°\right)=\mathrm{cot}\:{x}°\vdash\mathrm{tan}\left(\mathrm{90}^{°} −{x}°\right)=\mathrm{cot}\:{x}°,\mathrm{we}\:\mathrm{have}: \\ $$$$\mathrm{tan}\left(\mathrm{90}°−{k}°\right)=\mathrm{cot}\:{k}°=\frac{\mathrm{1}}{\mathrm{tan}\:{k}°} \\ $$$$\Rightarrow\mathrm{1}−\mathrm{tan}\left(\mathrm{90}°−{k}\right)=\mathrm{1}−\frac{\mathrm{1}}{\mathrm{tan}\:{k}°}=\frac{\mathrm{tan}\:{k}°−\mathrm{1}}{\mathrm{tan}\:{k}°} \\ $$$$\mathrm{Now}\:\mathrm{consider}\:\mathrm{the}\:\mathrm{product}: \\ $$$${P}\centerdot\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{tan}\:{k}°−\mathrm{1}}{\mathrm{tan}\:{k}°}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\left(\mathrm{1}+\mathrm{tan}\:{k}°\right)\centerdot\frac{\mathrm{tan}\:{k}°−\mathrm{1}}{\mathrm{tan}\:{k}°}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\left(\mathrm{tan}\:{k}°+\mathrm{1}\right)\left(\mathrm{tan}\:{k}°−\mathrm{1}\right)}{\mathrm{tan}\:{k}°} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{tan}^{\mathrm{2}} {k}°−\mathrm{1}}{\mathrm{tan}\:{k}°} \\ $$$$\mathrm{tan}\left(\mathrm{45}°+{x}°\right)=\frac{\mathrm{1}+\mathrm{tan}\:{x}°}{\mathrm{1}−\mathrm{tan}{x}°}\:\vdash\mathrm{tan}\left(\mathrm{45}^{°} +{k}°\right)\centerdot\mathrm{tan}\left(\mathrm{45}°−{k}°\right)=\mathrm{1} \\ $$$$\Rightarrow\mathrm{tan}\left(\mathrm{45}°+{k}°\right)=\frac{\mathrm{1}}{\mathrm{tan}\left(\mathrm{45}°−{k}°\right)} \\ $$$$\mathrm{This}\:\mathrm{implies}: \\ $$$$\mathrm{tan}\left(\mathrm{45}°+{k}°\right)\centerdot\mathrm{tan}\left(\mathrm{45}\centerdot{k}°\right)=\frac{\mathrm{1}+\mathrm{tan}\:{k}°}{\mathrm{1}−\mathrm{tan}\:{k}}\centerdot\frac{\mathrm{1}−\mathrm{tan}\:{k}}{\mathrm{1}+\mathrm{tan}\:{k}}=\mathrm{1} \\ $$$$\mathrm{so},\Pi\:\mathrm{simplifies}\:\mathrm{to}: \\ $$$${P}\centerdot\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{tan}\:{k}°−\mathrm{1}}{\mathrm{tan}\:{k}°}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{tan}^{\mathrm{2}} {k}°−\mathrm{1}}{\mathrm{tan}\:{k}°}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\mathrm{tan}\left(\mathrm{45}^{°} +{k}°\right)\centerdot\mathrm{tan}\left(\mathrm{45}°−{k}°\right) \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\mathrm{1}=\mathrm{1} \\ $$$$\mathrm{so},{P}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{tan}\:{k}°}{\mathrm{tan}\:{k}°−\mathrm{1}},\mathrm{Now}\:\mathrm{consider}: \\ $$$$\frac{{P}}{{Q}}=\frac{\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\left(\mathrm{1}+\mathrm{tan}\:{k}°\right)}{\underset{{k}=\mathrm{46}} {\overset{\mathrm{89}} {\prod}}\left(\mathrm{1}−\mathrm{tan}\:{k}°\right)}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{1}+\mathrm{tan}\:{k}°}{\mathrm{1}−\mathrm{tan}\left(\mathrm{90}°−{k}°\right)} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{1}+\mathrm{tan}\:{k}°}{\mathrm{1}−\mathrm{cot}\:{k}°}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{1}+\mathrm{tan}\:{k}°}{\frac{\mathrm{1}−\mathrm{tan}\:{k}°}{\mathrm{tan}\:{k}°}} \\ $$$$=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\frac{\mathrm{tan}\:{k}°\left(\mathrm{1}+\mathrm{tan}\:{k}°\right)}{\mathrm{1}−\mathrm{tan}\:{k}°} \\ $$$$\mathrm{tan}\left(\mathrm{45}°+{x}°\right)=\frac{\mathrm{1}+\mathrm{tan}\:{x}°}{\mathrm{1}−\mathrm{tan}\:{x}°}\:\vdash\mathrm{tan}\left(\mathrm{45}°+{k}^{°} \right)=\frac{\mathrm{1}+\mathrm{tan}\:{k}°}{\mathrm{1}−\mathrm{tan}\:{k}°} \\ $$$$\Rightarrow\frac{{P}}{{Q}}=\underset{{k}=\mathrm{1}} {\overset{\mathrm{44}} {\prod}}\mathrm{tan}\left(\mathrm{45}°+{k}°\right)=\mathrm{tan}\left(\mathrm{45}°+\mathrm{1}°\right)\centerdot\mathrm{tan}\left(\mathrm{45}+°\mathrm{2}\right)\centerdot\ldots\centerdot\mathrm{tan}\left(\mathrm{45}°+\mathrm{44}°\right) \\ $$$$\because\mathrm{tan}\left(\mathrm{45}°+{x}°\right)=\frac{\mathrm{1}+\mathrm{tan}\:{x}°}{\mathrm{1}−\mathrm{tan}\:{x}}\Rightarrow\frac{{P}}{{Q}}=\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{1}}{\mathrm{1}−\mathrm{tan}\:\mathrm{1}°}\centerdot\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{2}°}{\mathrm{1}−\mathrm{tan}\:\mathrm{2}°}\centerdot\ldots\centerdot\frac{\mathrm{1}+\mathrm{tan}\:\mathrm{44}°}{\mathrm{1}−\mathrm{tan}\:\mathrm{44}°} \\ $$$$\mathrm{so},=\begin{array}{|c|}{\mathrm{1}}\\\hline\end{array} \\ $$

Commented by hardmath last updated on 23/Feb/25

Excellent solution, thank you very much dear professor

$$ \\ $$Excellent solution, thank you very much dear professor

Terms of Service

Privacy Policy

Contact: info@tinkutara.com