Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 215893 by hardmath last updated on 20/Jan/25

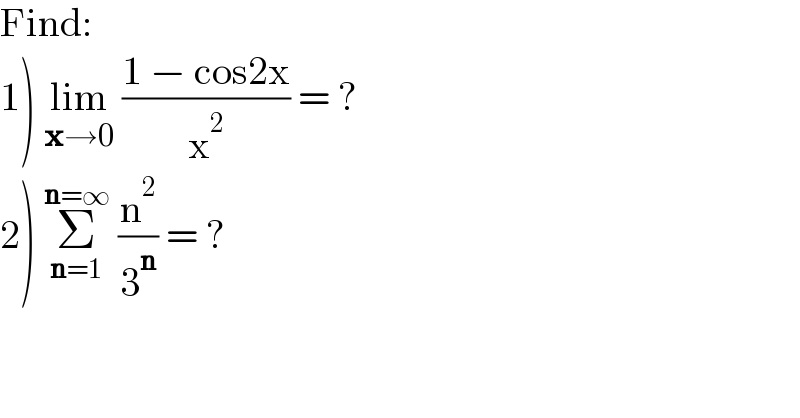
Find: 1) lim_(x→0) ((1 − cos2x)/x^2 ) = ? 2) Σ_(n=1) ^(n=∞) (n^2 /3^n ) = ?

$$\mathrm{Find}: \\ $$$$\left.\mathrm{1}\right)\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{1}\:−\:\mathrm{cos2x}}{\mathrm{x}^{\mathrm{2}} }\:=\:? \\ $$$$\left.\mathrm{2}\right)\:\underset{\boldsymbol{\mathrm{n}}=\mathrm{1}} {\overset{\boldsymbol{\mathrm{n}}=\infty} {\sum}}\:\frac{\mathrm{n}^{\mathrm{2}} }{\mathrm{3}^{\boldsymbol{\mathrm{n}}} }\:=\:? \\ $$

Answered by mathmax last updated on 23/Jan/25

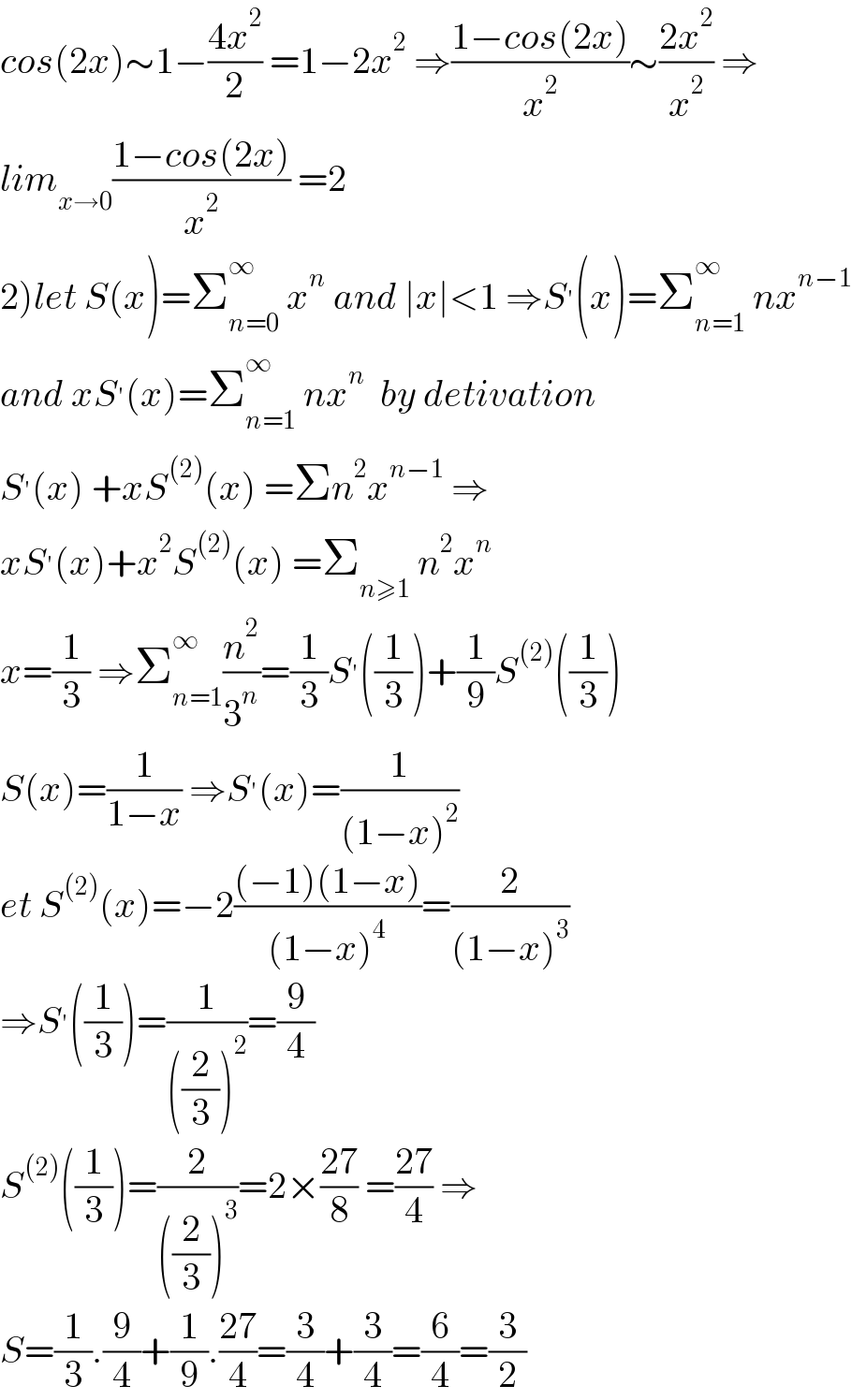
cos(2x)∼1−((4x^2 )/2) =1−2x^2 ⇒((1−cos(2x))/x^2 )∼((2x^2 )/x^2 ) ⇒ lim_(x→0) ((1−cos(2x))/x^2 ) =2 2)let S(x)=Σ_(n=0) ^∞ x^n and ∣x∣<1 ⇒S^′ (x)=Σ_(n=1) ^∞ nx^(n−1) and xS^′ (x)=Σ_(n=1) ^∞ nx^n by detivation S^′ (x) +xS^((2)) (x) =Σn^2 x^(n−1) ⇒ xS^′ (x)+x^2 S^((2)) (x) =Σ_(n≥1) n^2 x^n x=(1/3) ⇒Σ_(n=1) ^∞ (n^2 /3^n )=(1/3)S^′ ((1/3))+(1/9)S^((2)) ((1/3)) S(x)=(1/(1−x)) ⇒S^′ (x)=(1/((1−x)^2 )) et S^((2)) (x)=−2(((−1)(1−x))/((1−x)^4 ))=(2/((1−x)^3 )) ⇒S^′ ((1/3))=(1/(((2/3))^2 ))=(9/4) S^((2)) ((1/3))=(2/(((2/3))^3 ))=2×((27)/8) =((27)/4) ⇒ S=(1/3).(9/4)+(1/9).((27)/4)=(3/4)+(3/4)=(6/4)=(3/2)

$${cos}\left(\mathrm{2}{x}\right)\sim\mathrm{1}−\frac{\mathrm{4}{x}^{\mathrm{2}} }{\mathrm{2}}\:=\mathrm{1}−\mathrm{2}{x}^{\mathrm{2}} \:\Rightarrow\frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} }\sim\frac{\mathrm{2}{x}^{\mathrm{2}} }{{x}^{\mathrm{2}} }\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \frac{\mathrm{1}−{cos}\left(\mathrm{2}{x}\right)}{{x}^{\mathrm{2}} }\:=\mathrm{2} \\ $$$$\left.\mathrm{2}\right){let}\:{S}\left({x}\right)=\sum_{{n}=\mathrm{0}} ^{\infty} \:{x}^{{n}} \:{and}\:\mid{x}\mid<\mathrm{1}\:\Rightarrow{S}^{'} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}−\mathrm{1}} \\ $$$${and}\:{xS}^{'} \left({x}\right)=\sum_{{n}=\mathrm{1}} ^{\infty} \:{nx}^{{n}} \:\:{by}\:{detivation} \\ $$$${S}^{'} \left({x}\right)\:+{xS}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\Sigma{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} \:\Rightarrow \\ $$$${xS}^{'} \left({x}\right)+{x}^{\mathrm{2}} {S}^{\left(\mathrm{2}\right)} \left({x}\right)\:=\sum_{{n}\geqslant\mathrm{1}} \:{n}^{\mathrm{2}} {x}^{{n}} \:\:\: \\ $$$${x}=\frac{\mathrm{1}}{\mathrm{3}}\:\Rightarrow\sum_{{n}=\mathrm{1}} ^{\infty} \frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }=\frac{\mathrm{1}}{\mathrm{3}}{S}^{'} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)+\frac{\mathrm{1}}{\mathrm{9}}{S}^{\left(\mathrm{2}\right)} \left(\frac{\mathrm{1}}{\mathrm{3}}\right) \\ $$$${S}\left({x}\right)=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow{S}^{'} \left({x}\right)=\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$${et}\:{S}^{\left(\mathrm{2}\right)} \left({x}\right)=−\mathrm{2}\frac{\left(−\mathrm{1}\right)\left(\mathrm{1}−{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{4}} }=\frac{\mathrm{2}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\Rightarrow{S}^{'} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{1}}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{2}} }=\frac{\mathrm{9}}{\mathrm{4}} \\ $$$${S}^{\left(\mathrm{2}\right)} \left(\frac{\mathrm{1}}{\mathrm{3}}\right)=\frac{\mathrm{2}}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} }=\mathrm{2}×\frac{\mathrm{27}}{\mathrm{8}}\:=\frac{\mathrm{27}}{\mathrm{4}}\:\Rightarrow \\ $$$${S}=\frac{\mathrm{1}}{\mathrm{3}}.\frac{\mathrm{9}}{\mathrm{4}}+\frac{\mathrm{1}}{\mathrm{9}}.\frac{\mathrm{27}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{4}}+\frac{\mathrm{3}}{\mathrm{4}}=\frac{\mathrm{6}}{\mathrm{4}}=\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Answered by AntonCWX last updated on 21/Jan/25

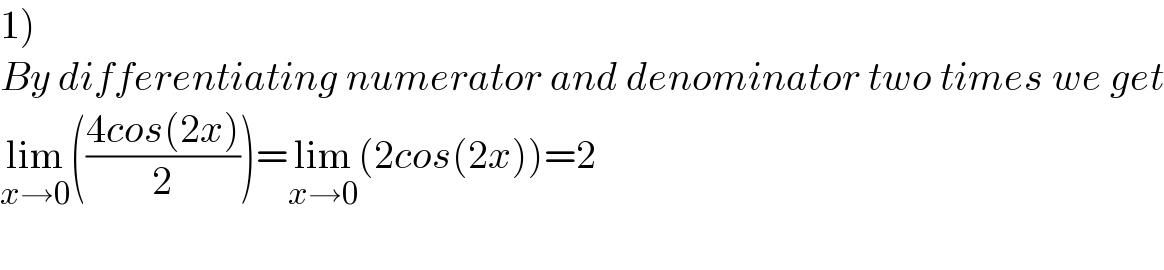
1) By differentiating numerator and denominator two times we get lim_(x→0) (((4cos(2x))/2))=lim_(x→0) (2cos(2x))=2

$$\left.\mathrm{1}\right) \\ $$$${By}\:{differentiating}\:{numerator}\:{and}\:{denominator}\:{two}\:{times}\:{we}\:{get} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{4}{cos}\left(\mathrm{2}{x}\right)}{\mathrm{2}}\right)=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\mathrm{2}{cos}\left(\mathrm{2}{x}\right)\right)=\mathrm{2} \\ $$$$ \\ $$

Commented by hardmath last updated on 21/Jan/25

1. Answer: 1

$$\mathrm{1}.\:\mathrm{Answer}:\:\mathrm{1} \\ $$

Commented by AntonCWX last updated on 21/Jan/25

Since you have the answer. I won′t bother to solve the second one.

$${Since}\:{you}\:{have}\:{the}\:{answer}. \\ $$$${I}\:{won}'{t}\:{bother}\:{to}\:{solve}\:{the}\:{second}\:{one}. \\ $$

Commented by mr W last updated on 21/Jan/25

to hardmath: you should show why the answer for 1) is 1. i think the solution and result from AntonCWX sir is correct.

$${to}\:{hardmath}: \\ $$$${you}\:{should}\:{show}\:{why}\:{the}\:{answer}\:{for} \\ $$$$\left.\mathrm{1}\right)\:{is}\:\mathrm{1}. \\ $$$${i}\:{think}\:{the}\:{solution}\:{and}\:{result}\:{from} \\ $$$${AntonCWX}\:{sir}\:{is}\:{correct}. \\ $$

Answered by mr W last updated on 21/Jan/25

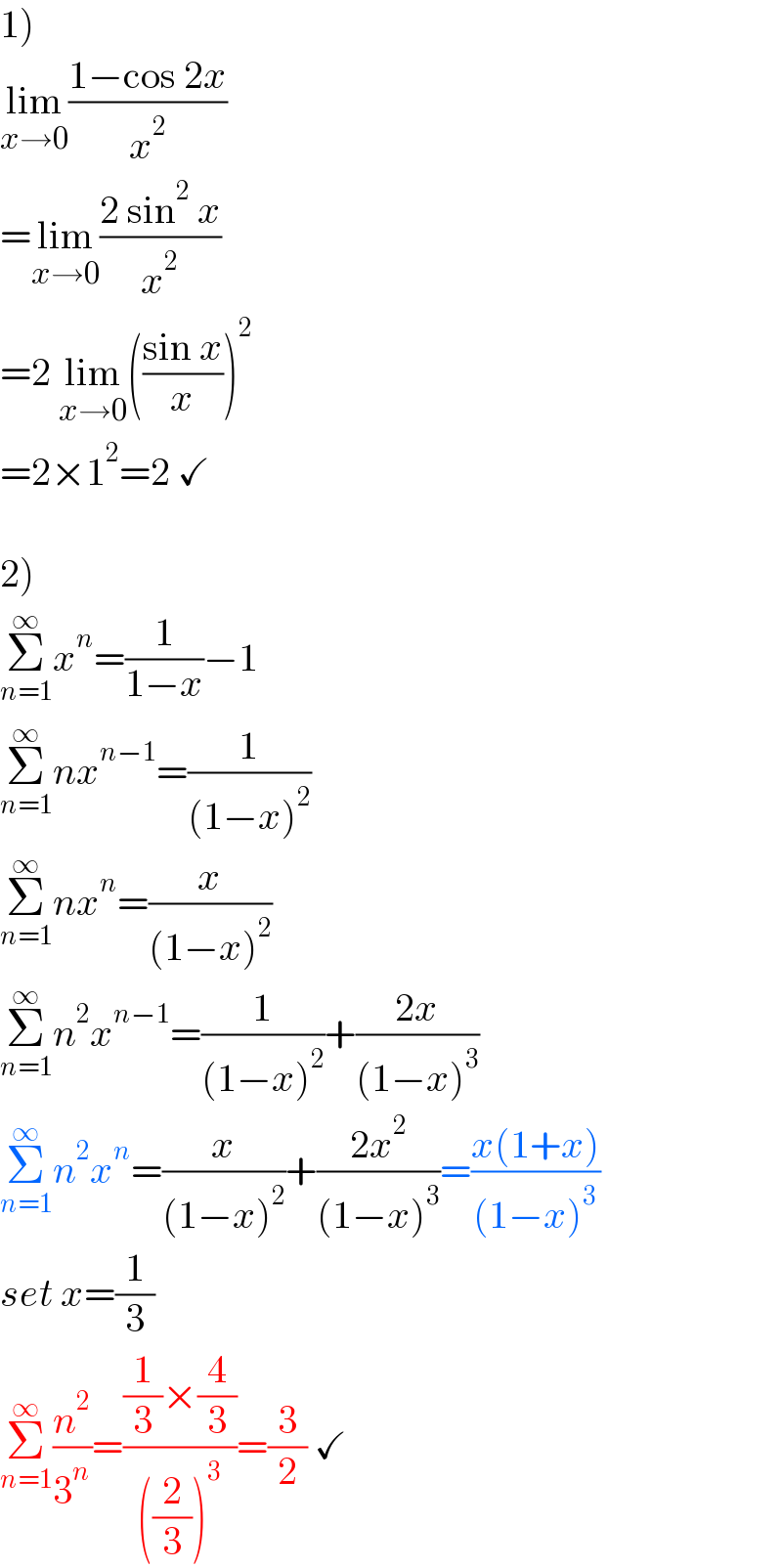
1) lim_(x→0) ((1−cos 2x)/x^2 ) =lim_(x→0) ((2 sin^2 x)/x^2 ) =2 lim_(x→0) (((sin x)/x))^2 =2×1^2 =2 ✓ 2) Σ_(n=1) ^∞ x^n =(1/(1−x))−1 Σ_(n=1) ^∞ nx^(n−1) =(1/((1−x)^2 )) Σ_(n=1) ^∞ nx^n =(x/((1−x)^2 )) Σ_(n=1) ^∞ n^2 x^(n−1) =(1/((1−x)^2 ))+((2x)/((1−x)^3 )) Σ_(n=1) ^∞ n^2 x^n =(x/((1−x)^2 ))+((2x^2 )/((1−x)^3 ))=((x(1+x))/((1−x)^3 )) set x=(1/3) Σ_(n=1) ^∞ (n^2 /3^n )=(((1/3)×(4/3))/(((2/3))^3 ))=(3/2) ✓

$$\left.\mathrm{1}\right) \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{1}−\mathrm{cos}\:\mathrm{2}{x}}{{x}^{\mathrm{2}} } \\ $$$$=\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\frac{\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:{x}}{{x}^{\mathrm{2}} } \\ $$$$=\mathrm{2}\:\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\left(\frac{\mathrm{sin}\:{x}}{{x}}\right)^{\mathrm{2}} \\ $$$$=\mathrm{2}×\mathrm{1}^{\mathrm{2}} =\mathrm{2}\:\checkmark \\ $$$$ \\ $$$$\left.\mathrm{2}\right) \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{{n}} =\frac{\mathrm{1}}{\mathrm{1}−{x}}−\mathrm{1} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{nx}^{{n}} =\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}−\mathrm{1}} =\frac{\mathrm{1}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}{n}^{\mathrm{2}} {x}^{{n}} =\frac{{x}}{\left(\mathrm{1}−{x}\right)^{\mathrm{2}} }+\frac{\mathrm{2}{x}^{\mathrm{2}} }{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} }=\frac{{x}\left(\mathrm{1}+{x}\right)}{\left(\mathrm{1}−{x}\right)^{\mathrm{3}} } \\ $$$${set}\:{x}=\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{{n}^{\mathrm{2}} }{\mathrm{3}^{{n}} }=\frac{\frac{\mathrm{1}}{\mathrm{3}}×\frac{\mathrm{4}}{\mathrm{3}}}{\left(\frac{\mathrm{2}}{\mathrm{3}}\right)^{\mathrm{3}} }=\frac{\mathrm{3}}{\mathrm{2}}\:\checkmark \\ $$

Answered by MathematicalUser2357 last updated on 21/Jan/25

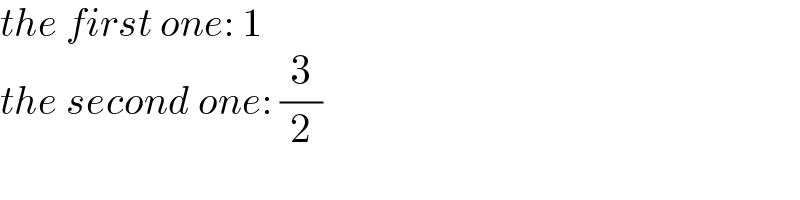
the first one: 1 the second one: (3/2)

$${the}\:{first}\:{one}:\:\mathrm{1} \\ $$$${the}\:{second}\:{one}:\:\frac{\mathrm{3}}{\mathrm{2}} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com