Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 192149 by Shrinava last updated on 09/May/23

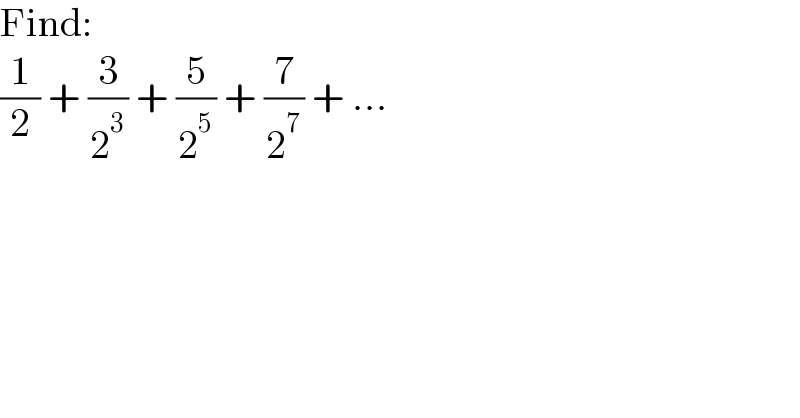
Find: (1/2) + (3/2^3 ) + (5/2^5 ) + (7/2^7 ) + ...

$$\mathrm{Find}: \\ $$$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }\:+\:\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }\:+\:\frac{\mathrm{7}}{\mathrm{2}^{\mathrm{7}} }\:+\:... \\ $$

Answered by aleks041103 last updated on 09/May/23

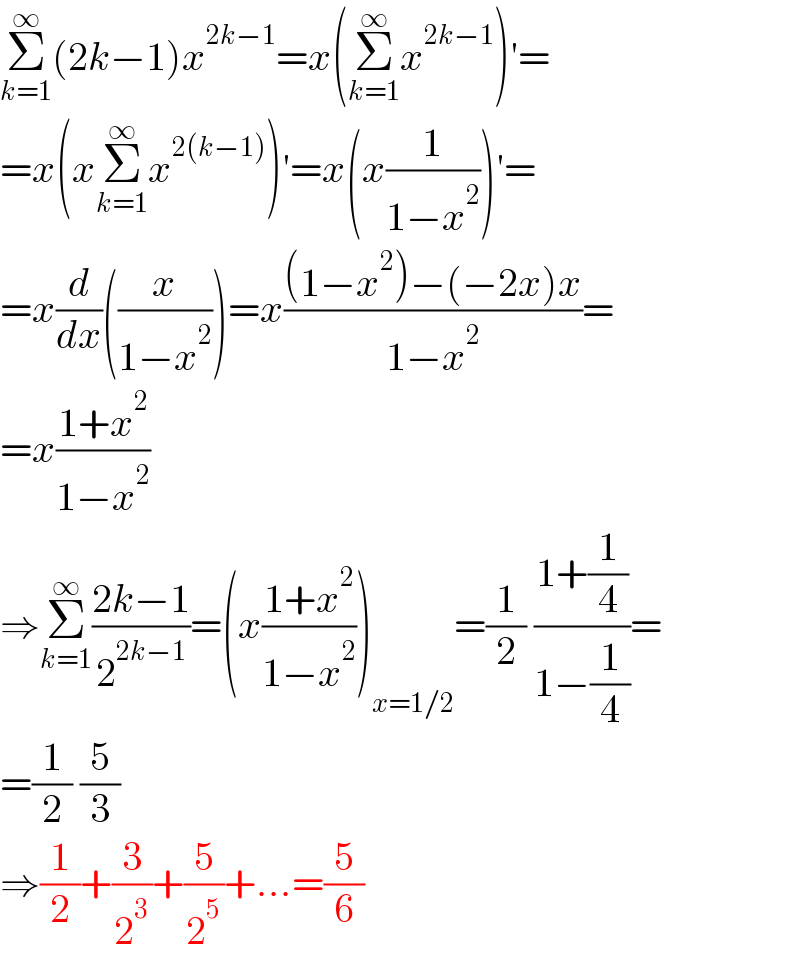
Σ_(k=1) ^∞ (2k−1)x^(2k−1) =x(Σ_(k=1) ^∞ x^(2k−1) )′= =x(xΣ_(k=1) ^∞ x^(2(k−1)) )′=x(x(1/(1−x^2 )))′= =x(d/dx)((x/(1−x^2 )))=x(((1−x^2 )−(−2x)x)/(1−x^2 ))= =x((1+x^2 )/(1−x^2 )) ⇒Σ_(k=1) ^∞ ((2k−1)/2^(2k−1) )=(x((1+x^2 )/(1−x^2 )))_(x=1/2) =(1/2) ((1+(1/4))/(1−(1/4)))= =(1/2) (5/3) ⇒(1/2)+(3/2^3 )+(5/2^5 )+...=(5/6)

$$\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\mathrm{2}{k}−\mathrm{1}\right){x}^{\mathrm{2}{k}−\mathrm{1}} ={x}\left(\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{\mathrm{2}{k}−\mathrm{1}} \right)'= \\ $$$$={x}\left({x}\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}{x}^{\mathrm{2}\left({k}−\mathrm{1}\right)} \right)'={x}\left({x}\frac{\mathrm{1}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)'= \\ $$$$={x}\frac{{d}}{{dx}}\left(\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)={x}\frac{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)−\left(−\mathrm{2}{x}\right){x}}{\mathrm{1}−{x}^{\mathrm{2}} }= \\ $$$$={x}\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} } \\ $$$$\Rightarrow\underset{{k}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}} }=\left({x}\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\mathrm{1}−{x}^{\mathrm{2}} }\right)_{{x}=\mathrm{1}/\mathrm{2}} =\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{1}+\frac{\mathrm{1}}{\mathrm{4}}}{\mathrm{1}−\frac{\mathrm{1}}{\mathrm{4}}}= \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\:\frac{\mathrm{5}}{\mathrm{3}} \\ $$$$\Rightarrow\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }+...=\frac{\mathrm{5}}{\mathrm{6}} \\ $$

Commented by deleteduser1 last updated on 09/May/23

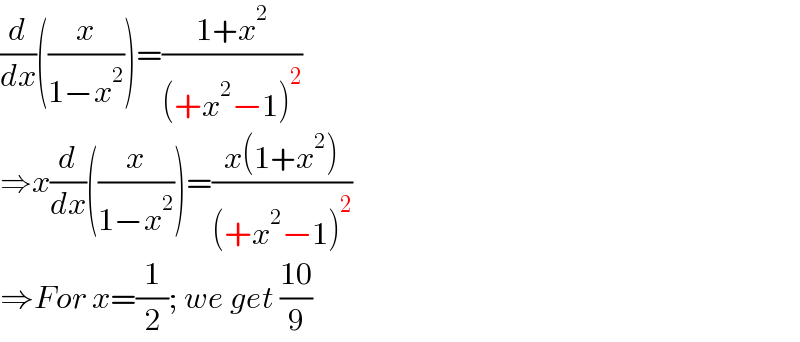
(d/dx)((x/(1−x^2 )))=((1+x^2 )/((+x^2 −1)^2 )) ⇒x(d/dx)((x/(1−x^2 )))=((x(1+x^2 ))/((+x^2 −1)^2 )) ⇒For x=(1/2); we get ((10)/9)

$$\frac{{d}}{{dx}}\left(\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\frac{\mathrm{1}+{x}^{\mathrm{2}} }{\left(+{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{x}\frac{{d}}{{dx}}\left(\frac{{x}}{\mathrm{1}−{x}^{\mathrm{2}} }\right)=\frac{{x}\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{\left(+{x}^{\mathrm{2}} −\mathrm{1}\right)^{\mathrm{2}} } \\ $$$$\Rightarrow{For}\:{x}=\frac{\mathrm{1}}{\mathrm{2}};\:{we}\:{get}\:\frac{\mathrm{10}}{\mathrm{9}} \\ $$

Commented by BaliramKumar last updated on 09/May/23

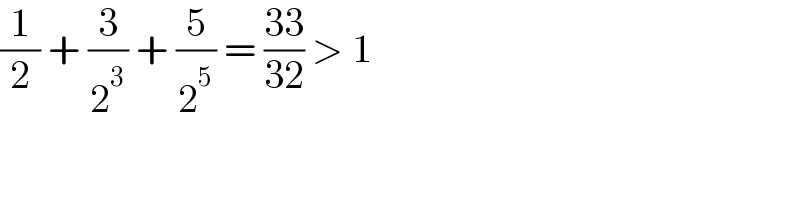
(1/2) + (3/2^3 ) + (5/2^5 ) = ((33)/(32)) > 1

$$\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }\:+\:\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }\:=\:\frac{\mathrm{33}}{\mathrm{32}}\:>\:\mathrm{1} \\ $$

Answered by mehdee42 last updated on 09/May/23

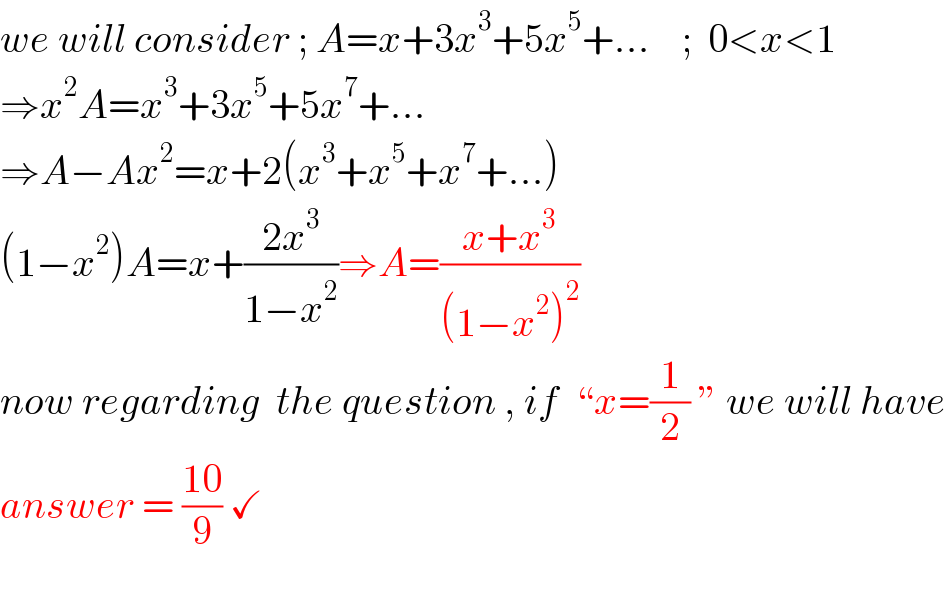
we will consider ; A=x+3x^3 +5x^5 +... ; 0<x<1 ⇒x^2 A=x^3 +3x^5 +5x^7 +... ⇒A−Ax^2 =x+2(x^3 +x^5 +x^7 +...) (1−x^2 )A=x+((2x^3 )/(1−x^2 ))⇒A=((x+x^3 )/((1−x^2 )^2 )) now regarding the question , if “x=(1/2) ” we will have answer = ((10)/9) ✓

$${we}\:{will}\:{consider}\:;\:{A}={x}+\mathrm{3}{x}^{\mathrm{3}} +\mathrm{5}{x}^{\mathrm{5}} +...\:\:\:\:;\:\:\mathrm{0}<{x}<\mathrm{1} \\ $$$$\Rightarrow{x}^{\mathrm{2}} {A}={x}^{\mathrm{3}} +\mathrm{3}{x}^{\mathrm{5}} +\mathrm{5}{x}^{\mathrm{7}} +... \\ $$$$\Rightarrow{A}−{Ax}^{\mathrm{2}} ={x}+\mathrm{2}\left({x}^{\mathrm{3}} +{x}^{\mathrm{5}} +{x}^{\mathrm{7}} +...\right) \\ $$$$\left(\mathrm{1}−{x}^{\mathrm{2}} \right){A}={x}+\frac{\mathrm{2}{x}^{\mathrm{3}} }{\mathrm{1}−{x}^{\mathrm{2}} }\Rightarrow{A}=\frac{{x}+{x}^{\mathrm{3}} }{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}} } \\ $$$${now}\:{regarding}\:\:{the}\:{question}\:,\:{if}\:\:``{x}=\frac{\mathrm{1}}{\mathrm{2}}\:''\:{we}\:{will}\:{have} \\ $$$${answer}\:=\:\frac{\mathrm{10}}{\mathrm{9}}\:\checkmark \\ $$$$ \\ $$

Answered by universe last updated on 09/May/23

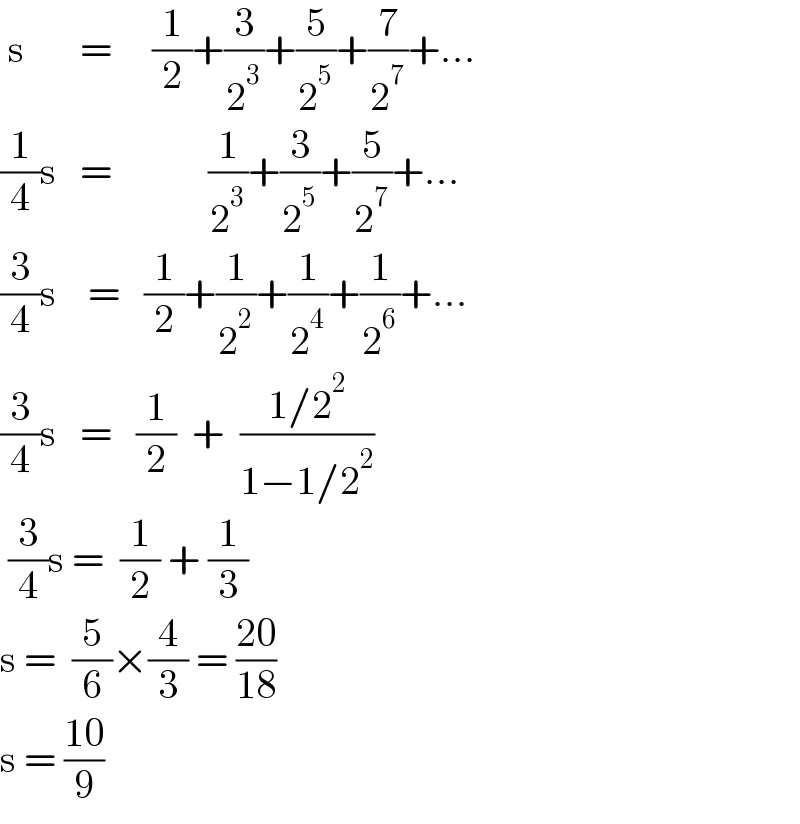
s = (1/2)+(3/2^3 )+(5/2^5 )+(7/2^7 )+... (1/4)s = (1/2^3 )+(3/2^5 )+(5/2^7 )+... (3/4)s = (1/2)+(1/2^2 )+(1/2^4 )+(1/2^6 )+... (3/4)s = (1/2) + ((1/2^2 )/(1−1/2^2 )) (3/4)s = (1/2) + (1/3) s = (5/6)×(4/3) = ((20)/(18)) s = ((10)/9)

$$\:\mathrm{s}\:\:\:\:\:\:\:=\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{5}} }+\frac{\mathrm{7}}{\mathrm{2}^{\mathrm{7}} }+... \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\mathrm{s}\:\:\:=\:\:\:\:\:\:\:\:\:\:\:\:\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{3}} }+\frac{\mathrm{3}}{\mathrm{2}^{\mathrm{5}} }+\frac{\mathrm{5}}{\mathrm{2}^{\mathrm{7}} }+... \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\mathrm{s}\:\:\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{2}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{4}} }+\frac{\mathrm{1}}{\mathrm{2}^{\mathrm{6}} }+... \\ $$$$\frac{\mathrm{3}}{\mathrm{4}}\mathrm{s}\:\:\:=\:\:\:\frac{\mathrm{1}}{\mathrm{2}}\:\:+\:\:\frac{\mathrm{1}/\mathrm{2}^{\mathrm{2}} }{\mathrm{1}−\mathrm{1}/\mathrm{2}^{\mathrm{2}} } \\ $$$$\:\frac{\mathrm{3}}{\mathrm{4}}\mathrm{s}\:=\:\:\frac{\mathrm{1}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{3}} \\ $$$$\mathrm{s}\:=\:\:\frac{\mathrm{5}}{\mathrm{6}}×\frac{\mathrm{4}}{\mathrm{3}}\:=\:\frac{\mathrm{20}}{\mathrm{18}} \\ $$$$\mathrm{s}\:=\:\frac{\mathrm{10}}{\mathrm{9}} \\ $$

Answered by York12 last updated on 09/May/23

that′s AGP

$${that}'{s}\:{AGP} \\ $$

Answered by manxsol last updated on 11/May/23

t_k =q ((2k−1)/2^(2k−1 ) )

$$\:{t}_{{k}} ={q}\:\:\:\:\:\frac{\mathrm{2}{k}−\mathrm{1}}{\mathrm{2}^{\mathrm{2}{k}−\mathrm{1}\:\:} } \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com