Question Number 159292 by HongKing last updated on 15/Nov/21
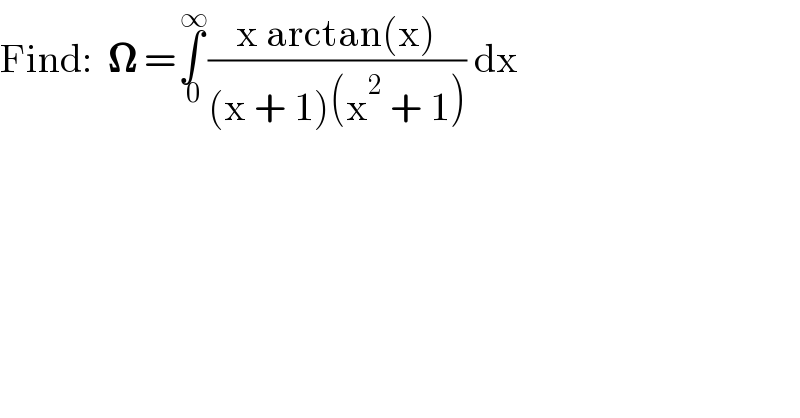
$$\mathrm{Find}:\:\:\boldsymbol{\Omega}\:=\underset{\:\mathrm{0}} {\overset{\:\infty} {\int}}\frac{\mathrm{x}\:\mathrm{arctan}\left(\mathrm{x}\right)}{\left(\mathrm{x}\:+\:\mathrm{1}\right)\left(\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{1}\right)}\:\mathrm{dx} \\ $$$$ \\ $$
Answered by mindispower last updated on 15/Nov/21
![=β«_0 ^β ((arctan(x))/(1+x^2 ))β((arctan(x))/((1+x)(1+x^2 )))dx =(Ο^2 /8)ββ«_0 ^(Ο/2) ((xcos(x))/(cos(x)+sin(x)))dxβ£_(=A) B=β«_0 ^(Ο/2) ((xsin(x))/(sin(x)+cos(x))) A+B=(Ο^2 /8) AβB=β«_0 ^(Ο/2) ((x(cos(x)βsin(x)))/(cos(x)+sin(x)))dx =[xln(cos(x)+sin(x))]_0 ^(Ο/2) ββ«_0 ^(Ο/2) ln(cos(x)+sin(x){dx =ββ«_0 ^(Ο/2) ln((β2)sin(x+(Ο/4)))d=β(Ο/2)ln((β2))ββ«_(Ο/4) ^((3Ο)/4) ln(sin(x))dx =ββ«_(Ο/4) ^(Ο/2) ln(sin(x))dxββ«_0 ^(Ο/4) lncos(x) =β2β«_0 ^(Ο/4) ln(cos(x))dx=β2.(1/4)(2GβΟln(2)) catalan constant A=(1/2)(AβB+A+B)=(1/2)((Ο^2 /8)β(Ο/2)ln((β2))βG+(Ο/2)ln(2)) =(Ο^2 /(16))+(Ο/8)ln(2)β(G/2) Ξ©=(Ο^2 /(16))+(G/2)β((Οln(2))/8)](Q159304.png)
$$=\int_{\mathrm{0}} ^{\infty} \frac{{arctan}\left({x}\right)}{\mathrm{1}+{x}^{\mathrm{2}} }β\frac{{arctan}\left({x}\right)}{\left(\mathrm{1}+{x}\right)\left(\mathrm{1}+{x}^{\mathrm{2}} \right)}{dx} \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{8}}β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{xcos}\left({x}\right)}{{cos}\left({x}\right)+{sin}\left({x}\right)}{dx}\mid_{={A}} \\ $$$${B}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{xsin}\left({x}\right)}{{sin}\left({x}\right)+{cos}\left({x}\right)} \\ $$$${A}+{B}=\frac{\pi^{\mathrm{2}} }{\mathrm{8}} \\ $$$${A}β{B}=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{x}\left({cos}\left({x}\right)β{sin}\left({x}\right)\right)}{{cos}\left({x}\right)+{sin}\left({x}\right)}{dx} \\ $$$$=\left[{xln}\left({cos}\left({x}\right)+{sin}\left({x}\right)\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({cos}\left({x}\right)+{sin}\left({x}\right)\left\{{dx}\right.\right. \\ $$$$=β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left(\sqrt{\mathrm{2}}{sin}\left({x}+\frac{\pi}{\mathrm{4}}\right)\right){d}=β\frac{\pi}{\mathrm{2}}{ln}\left(\sqrt{\mathrm{2}}\right)β\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\mathrm{3}\pi}{\mathrm{4}}} {ln}\left({sin}\left({x}\right)\right){dx} \\ $$$$=β\int_{\frac{\pi}{\mathrm{4}}} ^{\frac{\pi}{\mathrm{2}}} {ln}\left({sin}\left({x}\right)\right){dx}β\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {lncos}\left({x}\right) \\ $$$$=β\mathrm{2}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{4}}} {ln}\left({cos}\left({x}\right)\right){dx}=β\mathrm{2}.\frac{\mathrm{1}}{\mathrm{4}}\left(\mathrm{2}{G}β\pi{ln}\left(\mathrm{2}\right)\right) \\ $$$${catalan}\:{constant} \\ $$$${A}=\frac{\mathrm{1}}{\mathrm{2}}\left({A}β{B}+{A}+{B}\right)=\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{8}}β\frac{\pi}{\mathrm{2}}{ln}\left(\sqrt{\mathrm{2}}\right)β{G}+\frac{\pi}{\mathrm{2}}{ln}\left(\mathrm{2}\right)\right) \\ $$$$=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\frac{\pi}{\mathrm{8}}{ln}\left(\mathrm{2}\right)β\frac{{G}}{\mathrm{2}} \\ $$$$\Omega=\frac{\pi^{\mathrm{2}} }{\mathrm{16}}+\frac{{G}}{\mathrm{2}}β\frac{\pi{ln}\left(\mathrm{2}\right)}{\mathrm{8}} \\ $$$$ \\ $$
Commented by HongKing last updated on 15/Nov/21
$$\mathrm{cool}\:\mathrm{my}\:\mathrm{dear}\:\mathrm{Ser}\:\mathrm{thank}\:\mathrm{you}\:\mathrm{so}\:\mathrm{much} \\ $$
Commented by mindispower last updated on 15/Nov/21
$${you}\:{are}\:{welcom} \\ $$$${have}\:{a}\:{nice}\:{day} \\ $$$$ \\ $$
Commented by HongKing last updated on 15/Nov/21
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{my}\:\mathrm{dear}\:\boldsymbol{\mathrm{S}}\mathrm{er} \\ $$