Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 1780 by 112358 last updated on 23/Sep/15

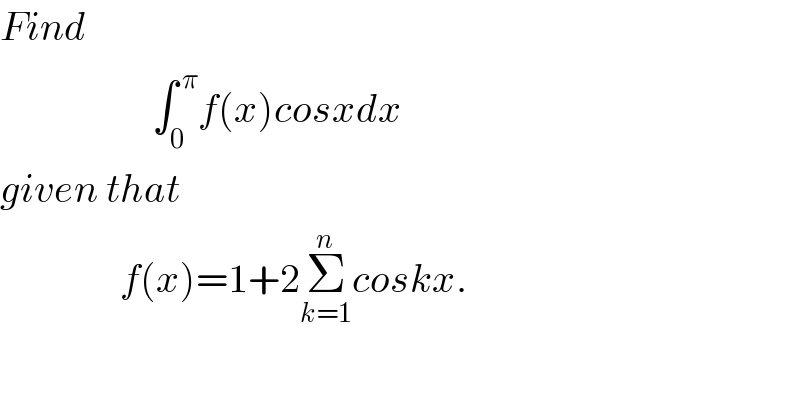
Find ∫_0 ^( π) f(x)cosxdx given that f(x)=1+2Σ_(k=1) ^n coskx.

$${Find}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\pi} {f}\left({x}\right){cosxdx} \\ $$$${given}\:{that}\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:{f}\left({x}\right)=\mathrm{1}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{coskx}.\: \\ $$

Commented by Rasheed Soomro last updated on 23/Sep/15

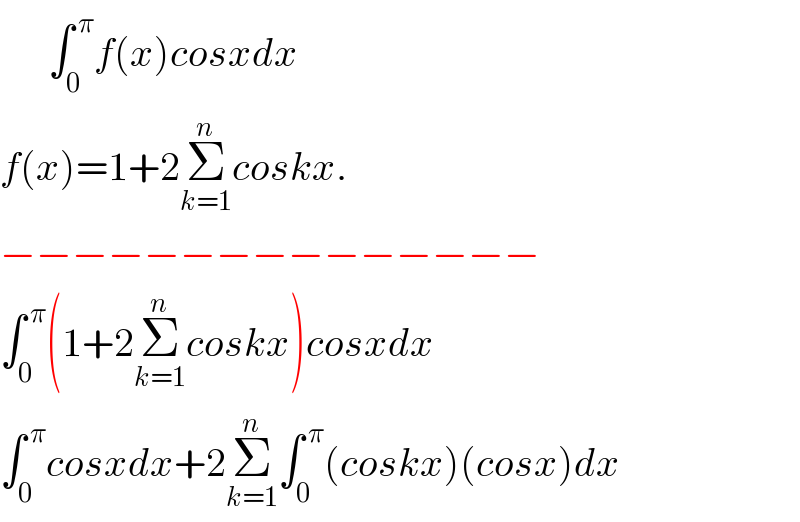
∫_0 ^( π) f(x)cosxdx f(x)=1+2Σ_(k=1) ^n coskx. −−−−−−−−−−−−−−− ∫_0 ^( π) (1+2Σ_(k=1) ^n coskx)cosxdx ∫_0 ^( π) cosxdx+2Σ_(k=1) ^n ∫_0 ^( π) (coskx)(cosx)dx

$$\:\:\:\:\:\:\int_{\mathrm{0}} ^{\:\pi} {f}\left({x}\right){cosxdx} \\ $$$${f}\left({x}\right)=\mathrm{1}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{coskx}.\: \\ $$$$−−−−−−−−−−−−−−− \\ $$$$\int_{\mathrm{0}} ^{\:\pi} \left(\mathrm{1}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}{coskx}\right){cosxdx} \\ $$$$\int_{\mathrm{0}} ^{\:\pi} {cosxdx}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\int_{\mathrm{0}} ^{\:\pi} \left({coskx}\right)\left({cosx}\right){dx} \\ $$

Answered by 123456 last updated on 24/Sep/15

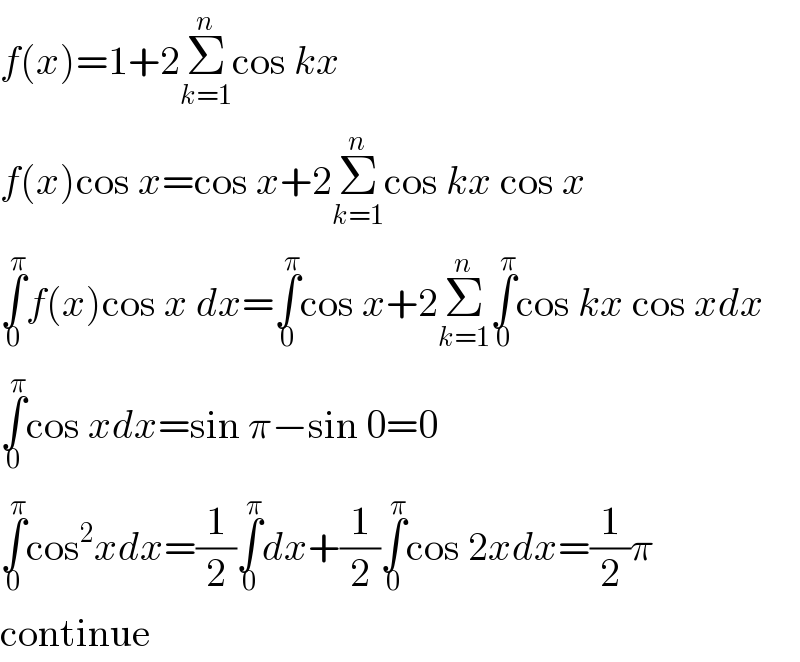
f(x)=1+2Σ_(k=1) ^n cos kx f(x)cos x=cos x+2Σ_(k=1) ^n cos kx cos x ∫_0 ^π f(x)cos x dx=∫_0 ^π cos x+2Σ_(k=1) ^n ∫_0 ^π cos kx cos xdx ∫_0 ^π cos xdx=sin π−sin 0=0 ∫_0 ^π cos^2 xdx=(1/2)∫_0 ^π dx+(1/2)∫_0 ^π cos 2xdx=(1/2)π continue

$${f}\left({x}\right)=\mathrm{1}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\:{kx} \\ $$$${f}\left({x}\right)\mathrm{cos}\:{x}=\mathrm{cos}\:{x}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\mathrm{cos}\:{kx}\:\mathrm{cos}\:{x} \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}{f}\left({x}\right)\mathrm{cos}\:{x}\:{dx}=\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{cos}\:{x}+\mathrm{2}\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{cos}\:{kx}\:\mathrm{cos}\:{xdx} \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{cos}\:{xdx}=\mathrm{sin}\:\pi−\mathrm{sin}\:\mathrm{0}=\mathrm{0}\: \\ $$$$\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{cos}^{\mathrm{2}} {xdx}=\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\pi} {\int}}{dx}+\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{0}} {\overset{\pi} {\int}}\mathrm{cos}\:\mathrm{2}{xdx}=\frac{\mathrm{1}}{\mathrm{2}}\pi \\ $$$$\mathrm{continue} \\ $$

Commented by 112358 last updated on 29/Sep/15

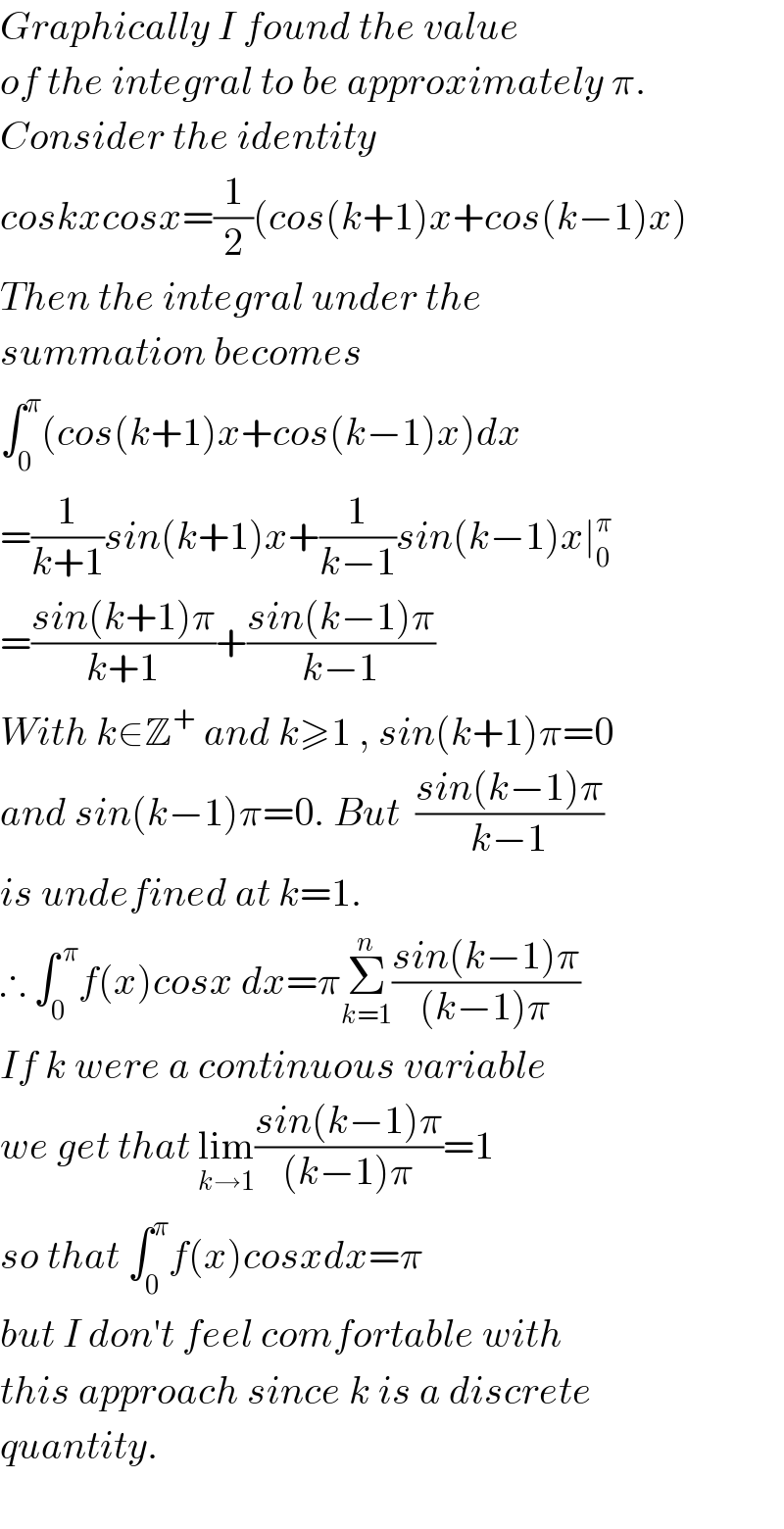
Graphically I found the value of the integral to be approximately π. Consider the identity coskxcosx=(1/2)(cos(k+1)x+cos(k−1)x) Then the integral under the summation becomes ∫_0 ^π (cos(k+1)x+cos(k−1)x)dx =(1/(k+1))sin(k+1)x+(1/(k−1))sin(k−1)x∣_0 ^π =((sin(k+1)π)/(k+1))+((sin(k−1)π)/(k−1)) With k∈Z^+ and k≥1 , sin(k+1)π=0 and sin(k−1)π=0. But ((sin(k−1)π)/(k−1)) is undefined at k=1. ∴ ∫_0 ^( π) f(x)cosx dx=πΣ_(k=1) ^n ((sin(k−1)π)/((k−1)π)) If k were a continuous variable we get that lim_(k→1) ((sin(k−1)π)/((k−1)π))=1 so that ∫_0 ^π f(x)cosxdx=π but I don′t feel comfortable with this approach since k is a discrete quantity.

$${Graphically}\:{I}\:{found}\:{the}\:{value} \\ $$$${of}\:{the}\:{integral}\:{to}\:{be}\:{approximately}\:\pi. \\ $$$${Consider}\:{the}\:{identity} \\ $$$${coskxcosx}=\frac{\mathrm{1}}{\mathrm{2}}\left({cos}\left({k}+\mathrm{1}\right){x}+{cos}\left({k}−\mathrm{1}\right){x}\right) \\ $$$${Then}\:{the}\:{integral}\:{under}\:{the}\: \\ $$$${summation}\:{becomes} \\ $$$$\int_{\mathrm{0}} ^{\pi} \left({cos}\left({k}+\mathrm{1}\right){x}+{cos}\left({k}−\mathrm{1}\right){x}\right){dx} \\ $$$$=\frac{\mathrm{1}}{{k}+\mathrm{1}}{sin}\left({k}+\mathrm{1}\right){x}+\frac{\mathrm{1}}{{k}−\mathrm{1}}{sin}\left({k}−\mathrm{1}\right){x}\mid_{\mathrm{0}} ^{\pi} \\ $$$$=\frac{{sin}\left({k}+\mathrm{1}\right)\pi}{{k}+\mathrm{1}}+\frac{{sin}\left({k}−\mathrm{1}\right)\pi}{{k}−\mathrm{1}} \\ $$$${With}\:{k}\in\mathbb{Z}^{+} \:{and}\:{k}\geqslant\mathrm{1}\:,\:{sin}\left({k}+\mathrm{1}\right)\pi=\mathrm{0} \\ $$$${and}\:{sin}\left({k}−\mathrm{1}\right)\pi=\mathrm{0}.\:{But}\:\:\frac{{sin}\left({k}−\mathrm{1}\right)\pi}{{k}−\mathrm{1}} \\ $$$${is}\:{undefined}\:{at}\:{k}=\mathrm{1}. \\ $$$$\therefore\:\int_{\mathrm{0}} ^{\:\pi} {f}\left({x}\right){cosx}\:{dx}=\pi\underset{{k}=\mathrm{1}} {\overset{{n}} {\sum}}\frac{{sin}\left({k}−\mathrm{1}\right)\pi}{\left({k}−\mathrm{1}\right)\pi} \\ $$$${If}\:{k}\:{were}\:{a}\:{continuous}\:{variable} \\ $$$${we}\:{get}\:{that}\:\underset{{k}\rightarrow\mathrm{1}} {\mathrm{lim}}\frac{{sin}\left({k}−\mathrm{1}\right)\pi}{\left({k}−\mathrm{1}\right)\pi}=\mathrm{1} \\ $$$${so}\:{that}\:\int_{\mathrm{0}} ^{\pi} {f}\left({x}\right){cosxdx}=\pi \\ $$$${but}\:{I}\:{don}'{t}\:{feel}\:{comfortable}\:{with} \\ $$$${this}\:{approach}\:{since}\:{k}\:{is}\:{a}\:{discrete} \\ $$$${quantity}. \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com