
Question Number 207170 by hardmath last updated on 08/May/24
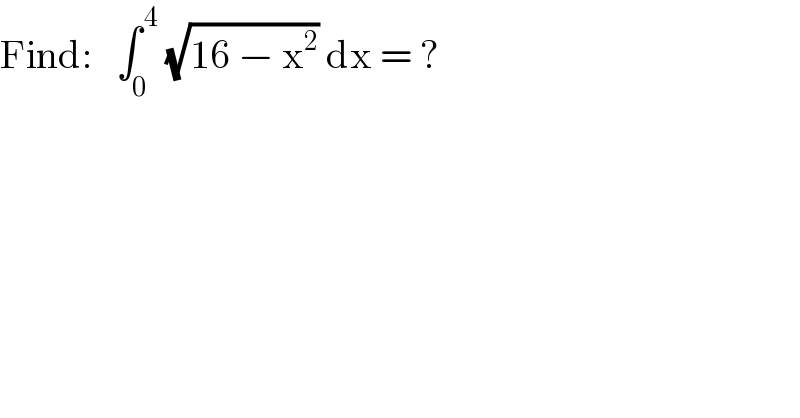
$$\mathrm{Find}:\:\:\:\int_{\mathrm{0}} ^{\:\mathrm{4}} \:\sqrt{\mathrm{16}\:−\:\mathrm{x}^{\mathrm{2}} }\:\mathrm{dx}\:=\:? \\ $$
Commented by MM42 last updated on 08/May/24
![x=4sinθ⇒dx=4cosθdθ ∫_0 ^(π/2) 16cos^2 θdθ=∫_0 ^(π/2) 8(1+cos2θ)dθ =8(θ+(1/2)sin2θ)]_0 ^(π/2) =4π ✓](Q207171.png)
$${x}=\mathrm{4}{sin}\theta\Rightarrow{dx}=\mathrm{4}{cos}\theta{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \:\mathrm{16}{cos}^{\mathrm{2}} \theta{d}\theta=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \mathrm{8}\left(\mathrm{1}+{cos}\mathrm{2}\theta\right){d}\theta \\ $$$$\left.=\mathrm{8}\left(\theta+\frac{\mathrm{1}}{\mathrm{2}}{sin}\mathrm{2}\theta\right)\right]_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \\ $$$$=\mathrm{4}\pi\:\:\checkmark \\ $$$$ \\ $$
Commented by hardmath last updated on 08/May/24

$$\mathrm{Answer}:\:\:\mathrm{4}\pi \\ $$
Commented by MM42 last updated on 08/May/24
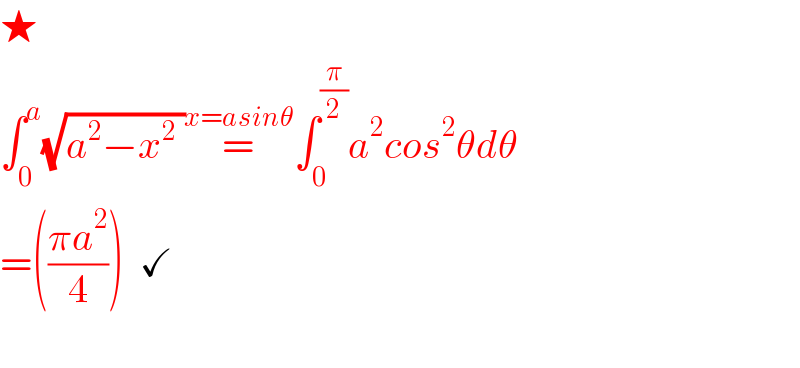
$$\bigstar \\ $$$$\int_{\mathrm{0}} ^{{a}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:}\overset{{x}={asin}\theta} {=}\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} {a}^{\mathrm{2}} {cos}^{\mathrm{2}} \theta{d}\theta \\ $$$$=\left(\frac{\pi{a}^{\mathrm{2}} }{\mathrm{4}}\right)\:\:\checkmark \\ $$$$ \\ $$
Commented by hardmath last updated on 10/May/24
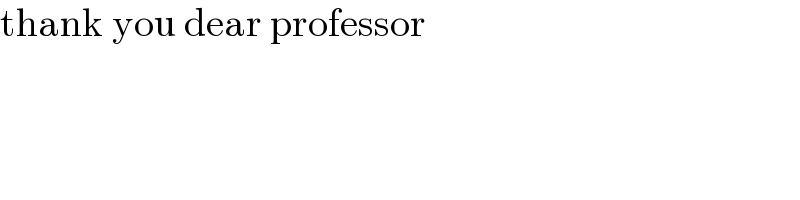
$$\mathrm{thank}\:\mathrm{you}\:\mathrm{dear}\:\mathrm{professor} \\ $$
Answered by Skabetix last updated on 09/May/24
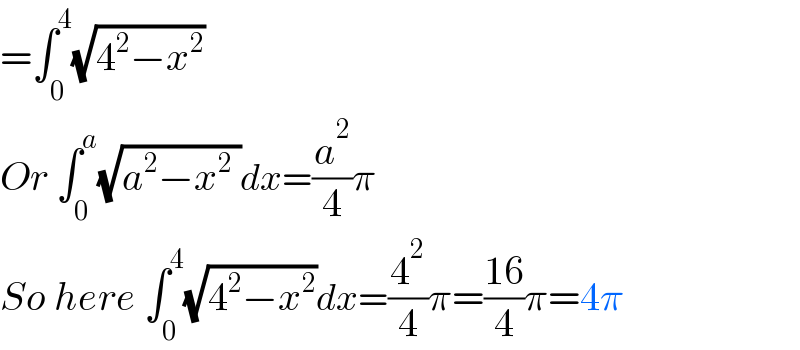
$$=\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{4}^{\mathrm{2}} −{x}^{\mathrm{2}} } \\ $$$${Or}\:\int_{\mathrm{0}} ^{{a}} \sqrt{{a}^{\mathrm{2}} −{x}^{\mathrm{2}} \:}{dx}=\frac{{a}^{\mathrm{2}} }{\mathrm{4}}\pi \\ $$$${So}\:{here}\:\int_{\mathrm{0}} ^{\mathrm{4}} \sqrt{\mathrm{4}^{\mathrm{2}} −{x}^{\mathrm{2}} }{dx}=\frac{\mathrm{4}^{\mathrm{2}} }{\mathrm{4}}\pi=\frac{\mathrm{16}}{\mathrm{4}}\pi=\mathrm{4}\pi \\ $$
