
Question Number 154994 by mathdanisur last updated on 24/Sep/21
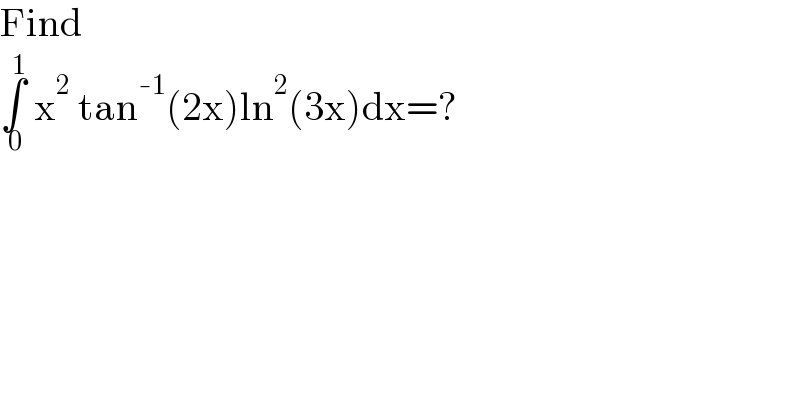
$$\mathrm{Find} \\ $$$$\underset{\:\mathrm{0}} {\overset{\:\mathrm{1}} {\int}}\:\mathrm{x}^{\mathrm{2}} \:\mathrm{tan}^{-\mathrm{1}} \left(\mathrm{2x}\right)\mathrm{ln}^{\mathrm{2}} \left(\mathrm{3x}\right)\mathrm{dx}=? \\ $$
Answered by phanphuoc last updated on 24/Sep/21
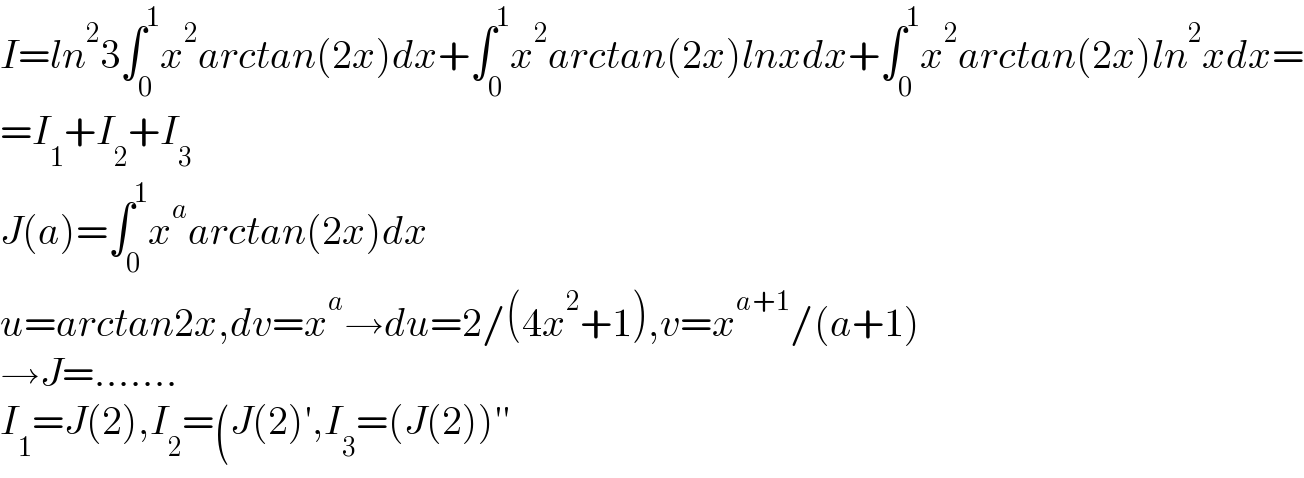
$${I}={ln}^{\mathrm{2}} \mathrm{3}\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {arctan}\left(\mathrm{2}{x}\right){dx}+\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {arctan}\left(\mathrm{2}{x}\right){lnxdx}+\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{\mathrm{2}} {arctan}\left(\mathrm{2}{x}\right){ln}^{\mathrm{2}} {xdx}= \\ $$$$={I}_{\mathrm{1}} +{I}_{\mathrm{2}} +{I}_{\mathrm{3}} \\ $$$${J}\left({a}\right)=\int_{\mathrm{0}} ^{\mathrm{1}} {x}^{{a}} {arctan}\left(\mathrm{2}{x}\right){dx} \\ $$$${u}={arctan}\mathrm{2}{x},{dv}={x}^{{a}} \rightarrow{du}=\mathrm{2}/\left(\mathrm{4}{x}^{\mathrm{2}} +\mathrm{1}\right),{v}={x}^{{a}+\mathrm{1}} /\left({a}+\mathrm{1}\right) \\ $$$$\rightarrow{J}=....... \\ $$$${I}_{\mathrm{1}} ={J}\left(\mathrm{2}\right),{I}_{\mathrm{2}} =\left({J}\left(\mathrm{2}\right)',{I}_{\mathrm{3}} =\left({J}\left(\mathrm{2}\right)\right)''\right. \\ $$
Commented by mathdanisur last updated on 24/Sep/21
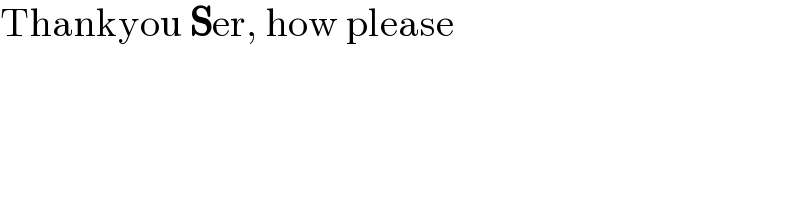
$$\mathrm{Thankyou}\:\boldsymbol{\mathrm{S}}\mathrm{er},\:\mathrm{how}\:\mathrm{please} \\ $$
