Question and Answers Forum

All Questions      Topic List

Algebra Questions

Previous in All Question      Next in All Question      

Previous in Algebra      Next in Algebra      

Question Number 174324 by BaliramKumar last updated on 29/Jul/22

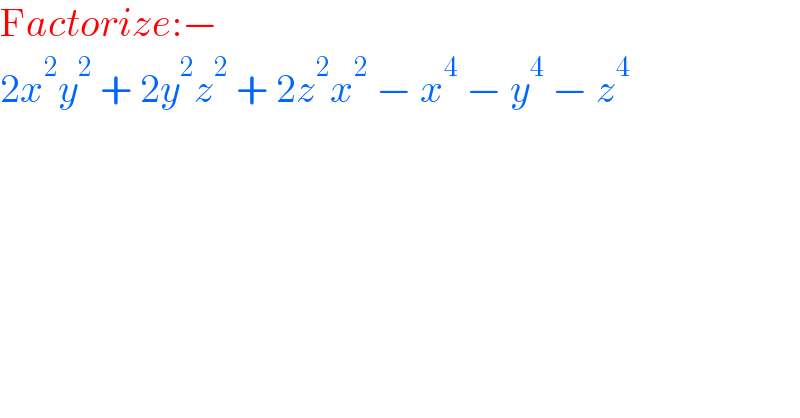
Factorize:− 2x^2 y^2 + 2y^2 z^2 + 2z^2 x^2 − x^4 − y^4 − z^4

$$\mathrm{F}{actorize}:− \\ $$$$\mathrm{2}{x}^{\mathrm{2}} {y}^{\mathrm{2}} \:+\:\mathrm{2}{y}^{\mathrm{2}} {z}^{\mathrm{2}} \:+\:\mathrm{2}{z}^{\mathrm{2}} {x}^{\mathrm{2}} \:−\:{x}^{\mathrm{4}} \:−\:{y}^{\mathrm{4}} \:−\:{z}^{\mathrm{4}} \\ $$

Commented by kaivan.ahmadi last updated on 30/Jul/22

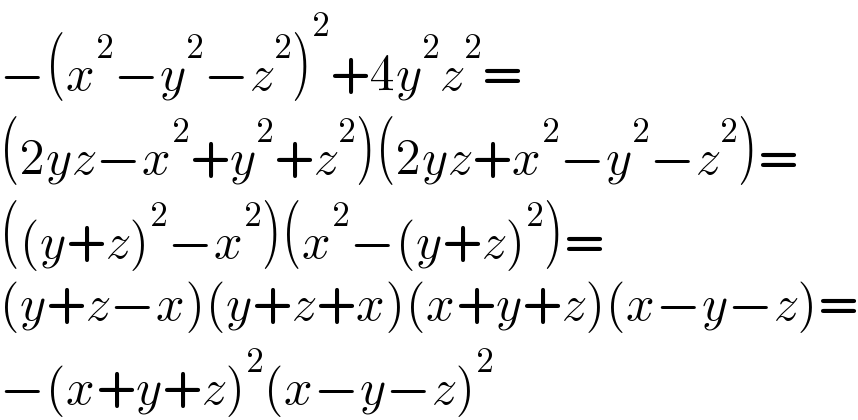
−(x^2 −y^2 −z^2 )^2 +4y^2 z^2 = (2yz−x^2 +y^2 +z^2 )(2yz+x^2 −y^2 −z^2 )= ((y+z)^2 −x^2 )(x^2 −(y+z)^2 )= (y+z−x)(y+z+x)(x+y+z)(x−y−z)= −(x+y+z)^2 (x−y−z)^2

$$−\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} {z}^{\mathrm{2}} = \\ $$$$\left(\mathrm{2}{yz}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\left(\mathrm{2}{yz}+{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)= \\ $$$$\left(\left({y}+{z}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\left({y}+{z}\right)^{\mathrm{2}} \right)= \\ $$$$\left({y}+{z}−{x}\right)\left({y}+{z}+{x}\right)\left({x}+{y}+{z}\right)\left({x}−{y}−{z}\right)= \\ $$$$−\left({x}+{y}+{z}\right)^{\mathrm{2}} \left({x}−{y}−{z}\right)^{\mathrm{2}} \\ $$

Commented by BaliramKumar last updated on 30/Jul/22

recheck answer

$${recheck}\:{answer}\: \\ $$

Commented by dragan91 last updated on 30/Jul/22

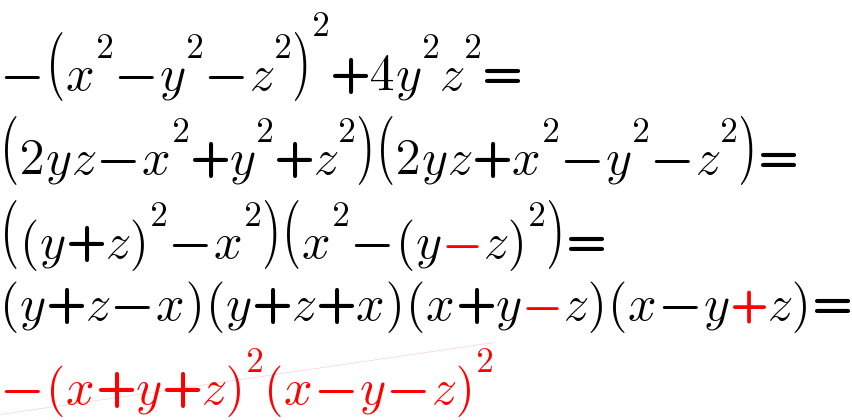
−(x^2 −y^2 −z^2 )^2 +4y^2 z^2 = (2yz−x^2 +y^2 +z^2 )(2yz+x^2 −y^2 −z^2 )= ((y+z)^2 −x^2 )(x^2 −(y−z)^2 )= (y+z−x)(y+z+x)(x+y−z)(x−y+z)= −(x+y+z)^2 (x−y−z)^2

$$−\left({x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)^{\mathrm{2}} +\mathrm{4}{y}^{\mathrm{2}} {z}^{\mathrm{2}} = \\ $$$$\left(\mathrm{2}{yz}−{x}^{\mathrm{2}} +{y}^{\mathrm{2}} +{z}^{\mathrm{2}} \right)\left(\mathrm{2}{yz}+{x}^{\mathrm{2}} −{y}^{\mathrm{2}} −{z}^{\mathrm{2}} \right)= \\ $$$$\left(\left({y}+{z}\right)^{\mathrm{2}} −{x}^{\mathrm{2}} \right)\left({x}^{\mathrm{2}} −\left({y}−{z}\right)^{\mathrm{2}} \right)= \\ $$$$\left({y}+{z}−{x}\right)\left({y}+{z}+{x}\right)\left({x}+{y}−{z}\right)\left({x}−{y}+{z}\right)= \\ $$$$\cancel{−\left({x}+{y}+{z}\right)^{\mathrm{2}} \left({x}−{y}−{z}\right)^{\mathrm{2}} } \\ $$

Commented by Frix last updated on 30/Jul/22

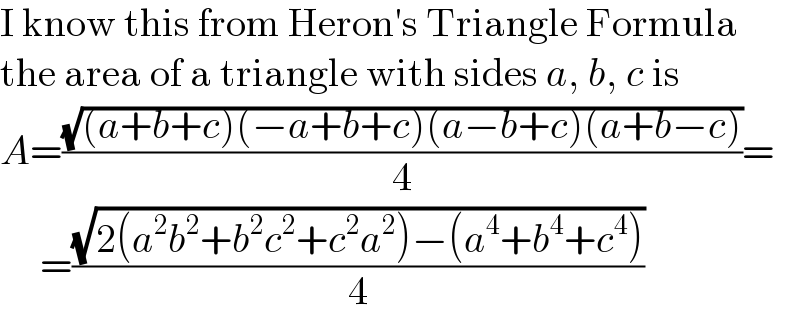
I know this from Heron′s Triangle Formula the area of a triangle with sides a, b, c is A=((√((a+b+c)(−a+b+c)(a−b+c)(a+b−c)))/4)= =((√(2(a^2 b^2 +b^2 c^2 +c^2 a^2 )−(a^4 +b^4 +c^4 )))/4)

$$\mathrm{I}\:\mathrm{know}\:\mathrm{this}\:\mathrm{from}\:\mathrm{Heron}'\mathrm{s}\:\mathrm{Triangle}\:\mathrm{Formula} \\ $$$$\mathrm{the}\:\mathrm{area}\:\mathrm{of}\:\mathrm{a}\:\mathrm{triangle}\:\mathrm{with}\:\mathrm{sides}\:{a},\:{b},\:{c}\:\mathrm{is} \\ $$$${A}=\frac{\sqrt{\left({a}+{b}+{c}\right)\left(−{a}+{b}+{c}\right)\left({a}−{b}+{c}\right)\left({a}+{b}−{c}\right)}}{\mathrm{4}}= \\ $$$$\:\:\:\:\:=\frac{\sqrt{\mathrm{2}\left({a}^{\mathrm{2}} {b}^{\mathrm{2}} +{b}^{\mathrm{2}} {c}^{\mathrm{2}} +{c}^{\mathrm{2}} {a}^{\mathrm{2}} \right)−\left({a}^{\mathrm{4}} +{b}^{\mathrm{4}} +{c}^{\mathrm{4}} \right)}}{\mathrm{4}} \\ $$

Commented by BaliramKumar last updated on 30/Jul/22

Yes sir

$${Yes}\:{sir} \\ $$

Answered by dragan91 last updated on 30/Jul/22

easy

$$\mathrm{easy} \\ $$

Answered by dragan91 last updated on 30/Jul/22

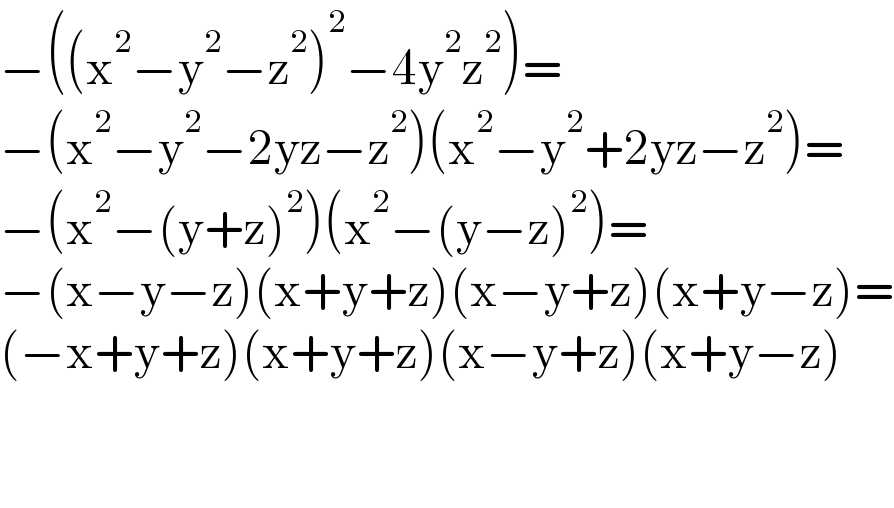
−((x^2 −y^2 −z^2 )^2 −4y^2 z^2 )= −(x^2 −y^2 −2yz−z^2 )(x^2 −y^2 +2yz−z^2 )= −(x^2 −(y+z)^2 )(x^2 −(y−z)^2 )= −(x−y−z)(x+y+z)(x−y+z)(x+y−z)= (−x+y+z)(x+y+z)(x−y+z)(x+y−z)

$$−\left(\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} −\mathrm{z}^{\mathrm{2}} \right)^{\mathrm{2}} −\mathrm{4y}^{\mathrm{2}} \mathrm{z}^{\mathrm{2}} \right)= \\ $$$$−\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} −\mathrm{2yz}−\mathrm{z}^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} +\mathrm{2yz}−\mathrm{z}^{\mathrm{2}} \right)= \\ $$$$−\left(\mathrm{x}^{\mathrm{2}} −\left(\mathrm{y}+\mathrm{z}\right)^{\mathrm{2}} \right)\left(\mathrm{x}^{\mathrm{2}} −\left(\mathrm{y}−\mathrm{z}\right)^{\mathrm{2}} \right)= \\ $$$$−\left(\mathrm{x}−\mathrm{y}−\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right)= \\ $$$$\left(−\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}−\mathrm{y}+\mathrm{z}\right)\left(\mathrm{x}+\mathrm{y}−\mathrm{z}\right) \\ $$$$ \\ $$$$ \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com