
Question Number 211370 by liuxinnan last updated on 07/Sep/24
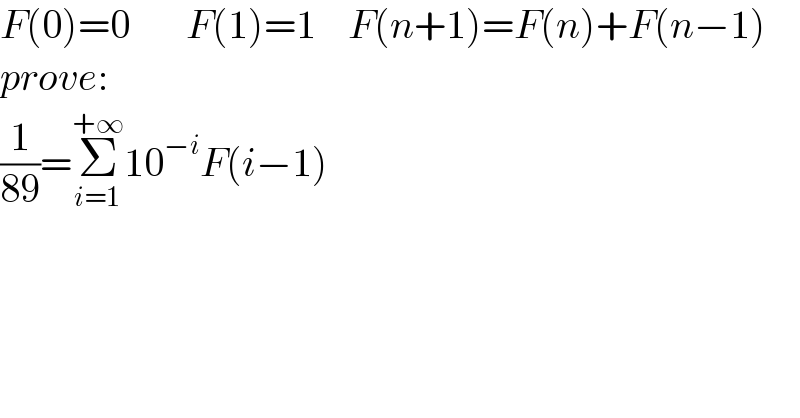
$${F}\left(\mathrm{0}\right)=\mathrm{0}\:\:\:\:\:\:\:{F}\left(\mathrm{1}\right)=\mathrm{1}\:\:\:\:{F}\left({n}+\mathrm{1}\right)={F}\left({n}\right)+{F}\left({n}−\mathrm{1}\right) \\ $$$${prove}: \\ $$$$\frac{\mathrm{1}}{\mathrm{89}}=\underset{{i}=\mathrm{1}} {\overset{+\infty} {\sum}}\mathrm{10}^{−{i}} {F}\left({i}−\mathrm{1}\right) \\ $$
Answered by mr W last updated on 07/Sep/24
![p^2 −p−1=0 ⇒p=((1±(√5))/2) ⇒F(n)=A(((1+(√5))/2))^n +B(((1−(√5))/2))^n F(0)=A+B=0⇒B=−A F(1)=A(((1+(√5))/2))−A(((1−(√5))/2))=1 ⇒A=(1/( (√5))) ⇒F(n)=(1/( (√5)))[(((1+(√5))/2))^n −(((1−(√5))/2))^n ] Σ_(n=1) ^∞ 10^(−n) F(n−1) =Σ_(n=0) ^∞ 10^(−(n+1)) F(n) =(1/(10(√5)))Σ_(n=0) ^∞ (1/(10^n ))[(((1+(√5))/2))^n −(((1−(√5))/2))^n ] =(1/(10(√5)))Σ_(n=0) ^∞ [(((1+(√5))/(20)))^n −(((1−(√5))/(20)))^n ] =(1/(10(√5)))((1/(1−((1+(√5))/(20))))−(1/(1−((1−(√5))/(20))))) =(2/( (√5)))(((19+(√5))/(356))−((19−(√5))/(356))) =(2/( (√5)))(((2(√5))/(356))) =(1/(89)) ✓](Q211371.png)
$${p}^{\mathrm{2}} −{p}−\mathrm{1}=\mathrm{0} \\ $$$$\Rightarrow{p}=\frac{\mathrm{1}\pm\sqrt{\mathrm{5}}}{\mathrm{2}} \\ $$$$\Rightarrow{F}\left({n}\right)={A}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} +{B}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \\ $$$${F}\left(\mathrm{0}\right)={A}+{B}=\mathrm{0}\Rightarrow{B}=−{A} \\ $$$${F}\left(\mathrm{1}\right)={A}\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)−{A}\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)=\mathrm{1}\:\Rightarrow{A}=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}} \\ $$$$\Rightarrow{F}\left({n}\right)=\frac{\mathrm{1}}{\:\sqrt{\mathrm{5}}}\left[\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \right] \\ $$$$\underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\mathrm{10}^{−{n}} {F}\left({n}−\mathrm{1}\right) \\ $$$$=\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{10}^{−\left({n}+\mathrm{1}\right)} {F}\left({n}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}\sqrt{\mathrm{5}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{10}^{{n}} }\left[\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{2}}\right)^{{n}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}\sqrt{\mathrm{5}}}\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left[\left(\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{20}}\right)^{{n}} −\left(\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{20}}\right)^{{n}} \right] \\ $$$$=\frac{\mathrm{1}}{\mathrm{10}\sqrt{\mathrm{5}}}\left(\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}+\sqrt{\mathrm{5}}}{\mathrm{20}}}−\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{1}−\sqrt{\mathrm{5}}}{\mathrm{20}}}\right) \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{19}+\sqrt{\mathrm{5}}}{\mathrm{356}}−\frac{\mathrm{19}−\sqrt{\mathrm{5}}}{\mathrm{356}}\right) \\ $$$$=\frac{\mathrm{2}}{\:\sqrt{\mathrm{5}}}\left(\frac{\mathrm{2}\sqrt{\mathrm{5}}}{\mathrm{356}}\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{89}}\:\checkmark \\ $$
Commented by liuxinnan last updated on 09/Sep/24

$${thanks}\:{sir} \\ $$
