
Question Number 104339 by bemath last updated on 21/Jul/20
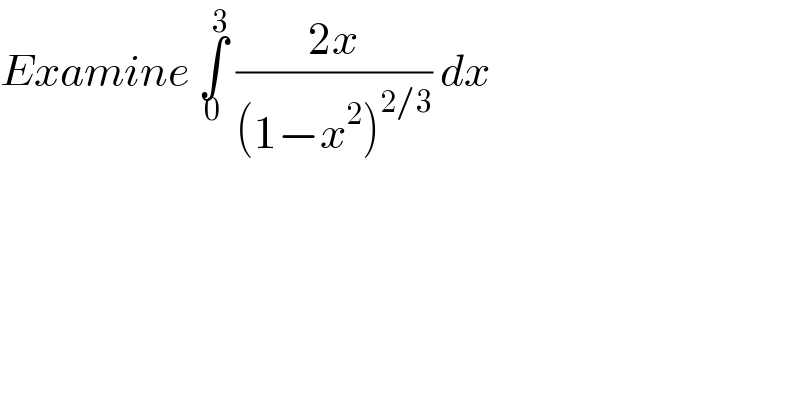
$${Examine}\:\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}/\mathrm{3}} }\:{dx} \\ $$
Commented by bemath last updated on 21/Jul/20

$${thank}\:{you}\:{both} \\ $$
Answered by Ar Brandon last updated on 21/Jul/20
![∫_0 ^3 ((2x)/((1−x^2 )^(2/3) )) dx=−∫_0 ^3 ((−2x)/((1−x^2 )^(2/3) )) dx =−∫_0 ^3 ((d(1−x^2 ))/((1−x^2 )^(2/3) ))=∫_(−8) ^1 u^(−2/3) du =[3(u)^(1/3) ]_(−8) ^1 =3+6=9](Q104340.png)
$$\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}/\mathrm{3}} }\:{dx}=−\underset{\mathrm{0}} {\overset{\mathrm{3}} {\int}}\:\frac{−\mathrm{2}{x}}{\left(\mathrm{1}−{x}^{\mathrm{2}} \right)^{\mathrm{2}/\mathrm{3}} }\:{dx} \\ $$$$=−\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\mathrm{d}\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\mathrm{2}/\mathrm{3}} }=\int_{−\mathrm{8}} ^{\mathrm{1}} \mathrm{u}^{−\mathrm{2}/\mathrm{3}} \mathrm{du} \\ $$$$=\left[\mathrm{3}\sqrt[{\mathrm{3}}]{\mathrm{u}}\right]_{−\mathrm{8}} ^{\mathrm{1}} =\mathrm{3}+\mathrm{6}=\mathrm{9} \\ $$
Answered by bramlex last updated on 21/Jul/20

Answered by Dwaipayan Shikari last updated on 21/Jul/20
![∫_0 ^3 ((2xdx)/((1−x^2 )^(2/3) ))=−∫_0 ^3 (dt/t^(2/3) )=−3[t^(1/3) ]_0 ^3 =−3[(1−x^2 )^(1/3) ]_0 ^3 =9](Q104387.png)
$$\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\mathrm{2xdx}}{\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{2}}{\mathrm{3}}} }=−\int_{\mathrm{0}} ^{\mathrm{3}} \frac{\mathrm{dt}}{\mathrm{t}^{\frac{\mathrm{2}}{\mathrm{3}}} }=−\mathrm{3}\left[\mathrm{t}^{\frac{\mathrm{1}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{3}} =−\mathrm{3}\left[\left(\mathrm{1}−\mathrm{x}^{\mathrm{2}} \right)^{\frac{\mathrm{1}}{\mathrm{3}}} \right]_{\mathrm{0}} ^{\mathrm{3}} =\mathrm{9} \\ $$
