
Question Number 179494 by a.lgnaoui last updated on 29/Oct/22
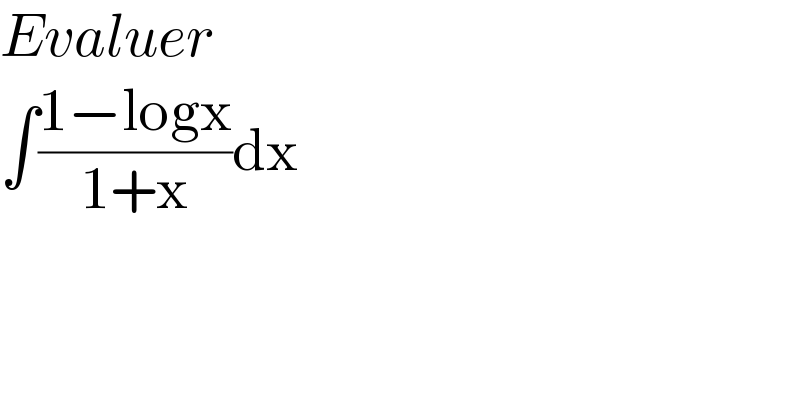
$${Evaluer} \\ $$$$\int\frac{\mathrm{1}−\mathrm{logx}}{\mathrm{1}+\mathrm{x}}\mathrm{dx} \\ $$
Answered by ARUNG_Brandon_MBU last updated on 29/Oct/22
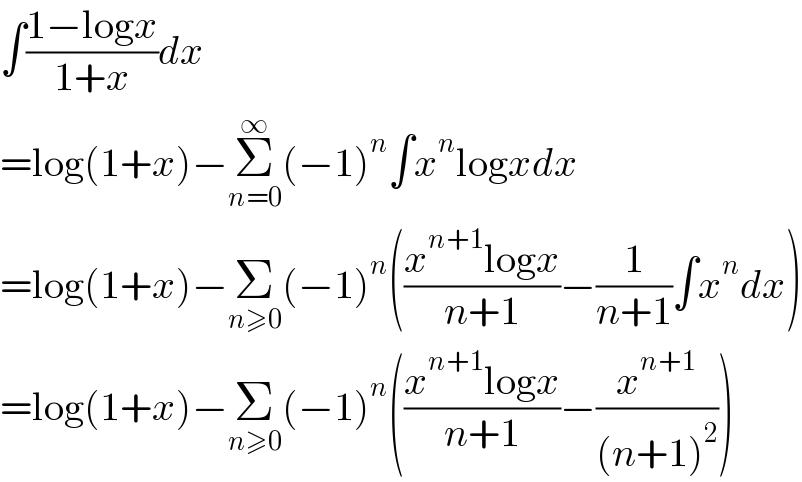
$$\int\frac{\mathrm{1}−\mathrm{log}{x}}{\mathrm{1}+{x}}{dx} \\ $$$$=\mathrm{log}\left(\mathrm{1}+{x}\right)−\underset{{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(−\mathrm{1}\right)^{{n}} \int{x}^{{n}} \mathrm{log}{xdx} \\ $$$$=\mathrm{log}\left(\mathrm{1}+{x}\right)−\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \left(\frac{{x}^{{n}+\mathrm{1}} \mathrm{log}{x}}{{n}+\mathrm{1}}−\frac{\mathrm{1}}{{n}+\mathrm{1}}\int{x}^{{n}} {dx}\right) \\ $$$$=\mathrm{log}\left(\mathrm{1}+{x}\right)−\underset{{n}\geqslant\mathrm{0}} {\sum}\left(−\mathrm{1}\right)^{{n}} \left(\frac{{x}^{{n}+\mathrm{1}} \mathrm{log}{x}}{{n}+\mathrm{1}}−\frac{{x}^{{n}+\mathrm{1}} }{\left({n}+\mathrm{1}\right)^{\mathrm{2}} }\right) \\ $$
Commented by a.lgnaoui last updated on 30/Oct/22
$${good}\:{thank}\:{you} \\ $$
