
Question Number 67471 by AnjanDey last updated on 27/Aug/19
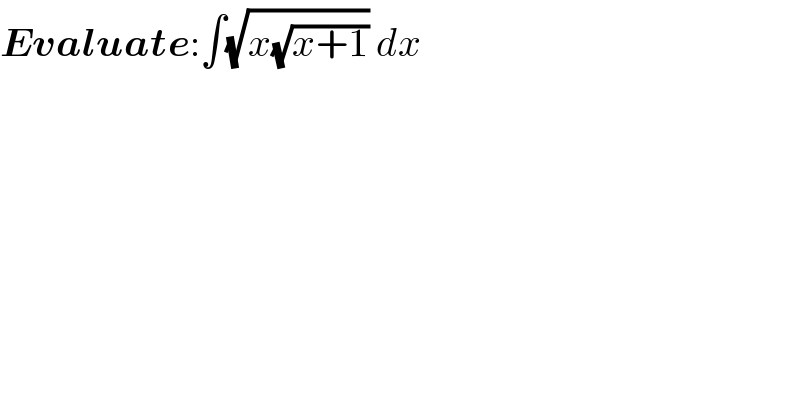
$$\boldsymbol{{Evaluate}}:\int\sqrt{{x}\sqrt{{x}+\mathrm{1}}}\:{dx} \\ $$
Commented by MJS last updated on 28/Aug/19
![∫(√(x(√(x+1))))dx= [t=(√x) → dx=2(√x)dt] =2∫t^2 (t^2 +1)^(1/4) dt= =−(4/(21))∫(dt/((t^2 +1)^(3/4) ))+2∫((t^4 +t^2 +(2/(21)))/((t^2 +1)^(3/4) ))dt =−(4/(21))∫(dt/((t^2 +1)^(3/4) ))+(4/(21))t(3t^2 +1)(t^2 +1)^(1/4) ...I cannot solve the 1^(st) one plus I somehow solved the 2^(nd) one but I really don′t remember how... I lost some papers... anyway (d/dt)[(4/(21))t(3t^2 +1)(t^2 +1)^(1/4) ]=2((t^4 +t^2 +(2/(21)))/((t^2 +1)^(3/4) )) and −(4/(21(t^2 +1)^(3/4) ))+2((t^4 +t^2 +(2/(21)))/((t^2 +1)^(3/4) ))=2t^2 (t^2 +1)^(1/4)](Q67490.png)
$$\int\sqrt{{x}\sqrt{{x}+\mathrm{1}}}{dx}= \\ $$$$\:\:\:\:\:\left[{t}=\sqrt{{x}}\:\rightarrow\:{dx}=\mathrm{2}\sqrt{{x}}{dt}\right] \\ $$$$=\mathrm{2}\int{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} {dt}= \\ $$$$=−\frac{\mathrm{4}}{\mathrm{21}}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }+\mathrm{2}\int\frac{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{21}}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }{dt} \\ $$$$=−\frac{\mathrm{4}}{\mathrm{21}}\int\frac{{dt}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }+\frac{\mathrm{4}}{\mathrm{21}}{t}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$$$...\mathrm{I}\:\mathrm{cannot}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{1}^{\mathrm{st}} \:\mathrm{one} \\ $$$$\mathrm{plus}\:\mathrm{I}\:\mathrm{somehow}\:\mathrm{solved}\:\mathrm{the}\:\mathrm{2}^{\mathrm{nd}} \:\mathrm{one}\:\mathrm{but}\:\mathrm{I}\:\mathrm{really} \\ $$$$\mathrm{don}'\mathrm{t}\:\mathrm{remember}\:\mathrm{how}...\:\mathrm{I}\:\mathrm{lost}\:\mathrm{some}\:\mathrm{papers}... \\ $$$$\mathrm{anyway}\:\frac{{d}}{{dt}}\left[\frac{\mathrm{4}}{\mathrm{21}}{t}\left(\mathrm{3}{t}^{\mathrm{2}} +\mathrm{1}\right)\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \right]=\mathrm{2}\frac{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{21}}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} } \\ $$$$\mathrm{and}\:−\frac{\mathrm{4}}{\mathrm{21}\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }+\mathrm{2}\frac{{t}^{\mathrm{4}} +{t}^{\mathrm{2}} +\frac{\mathrm{2}}{\mathrm{21}}}{\left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{3}}{\mathrm{4}}} }=\mathrm{2}{t}^{\mathrm{2}} \left({t}^{\mathrm{2}} +\mathrm{1}\right)^{\frac{\mathrm{1}}{\mathrm{4}}} \\ $$
Commented by Abdo msup. last updated on 28/Aug/19

$${let}\:{take}\:\:{a}\:{try}\:\:\:{we}\:{do}\:{the}\:{changement}\:\sqrt{{x}+\mathrm{1}}={t}\:\Rightarrow \\ $$$${x}+\mathrm{1}={t}^{\mathrm{2}} \:\Rightarrow{x}\:={t}^{\mathrm{2}} −\mathrm{1}\:\Rightarrow \\ $$$$\int\sqrt{{x}\sqrt{{x}+\mathrm{1}}}{dx}\:=\int\:\:\sqrt{\left({t}^{\mathrm{2}} −\mathrm{1}\right){t}}\left(\mathrm{2}{t}\right){dt} \\ $$$$=\mathrm{2}\:\int\:\:{t}\sqrt{{t}^{\mathrm{3}} −{t}}{dt}\:=\mathrm{2}\int\:{t}\sqrt{{t}\left({t}^{\mathrm{2}} −\mathrm{1}\right)}{dt} \\ $$$$=\mathrm{2}\:\int\:{t}^{\frac{\mathrm{3}}{\mathrm{2}}} \sqrt{{t}^{\mathrm{2}} −\mathrm{1}}{dt}\:\:\:{and}\:{changement}\:{t}\:={ch}\left({u}\right)\:{give} \\ $$$${I}\:=\mathrm{2}\:\int\:\:\:\left({chu}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} {sh}\left({u}\right){sh}\left({u}\right){du} \\ $$$${by}\:{psrts}\:\:\:{f}^{'} ={sh}\left({u}\right)\left({chu}\right)^{\frac{\mathrm{3}}{\mathrm{2}}} \:\:{and}\:{g}={shu} \\ $$$${I}\:=\frac{\mathrm{2}}{\mathrm{5}}\left({chu}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:{sh}\left({u}\right)−\int\:\:\frac{\mathrm{2}}{\mathrm{5}}\left({chu}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} \:{ch}\left({u}\right){du} \\ $$$$=\frac{\mathrm{2}}{\mathrm{5}}\left({chu}\right)^{\frac{\mathrm{5}}{\mathrm{2}}} −\frac{\mathrm{2}}{\mathrm{5}}\:\int\:\:\left({chu}\right)^{\frac{\mathrm{7}}{\mathrm{2}}} \:{du} \\ $$$${the}\:{probleme}\:{is}\:{how}\:{to}\:{calculate}\:{intehral}\:{at} \\ $$$${form}\:\int\:\:\left({chu}\right)^{{r}} {du}\:\:{with}\:{r}\:\in\:{Q}^{+} ?\:\:\:...{be}\:{continued}... \\ $$
Commented by Abdo msup. last updated on 28/Aug/19
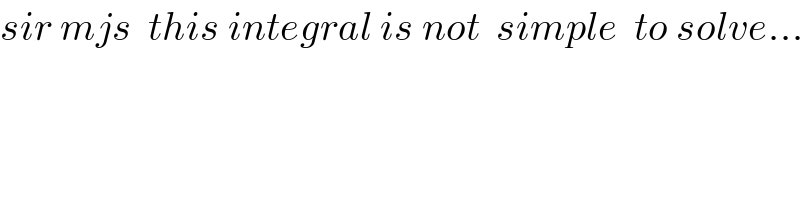
$${sir}\:{mjs}\:\:{this}\:{integral}\:{is}\:{not}\:\:{simple}\:\:{to}\:{solve}... \\ $$
Commented by MJS last updated on 28/Aug/19

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{for}\:\mathrm{trying} \\ $$
