
Question Number 76965 by peter frank last updated on 02/Jan/20
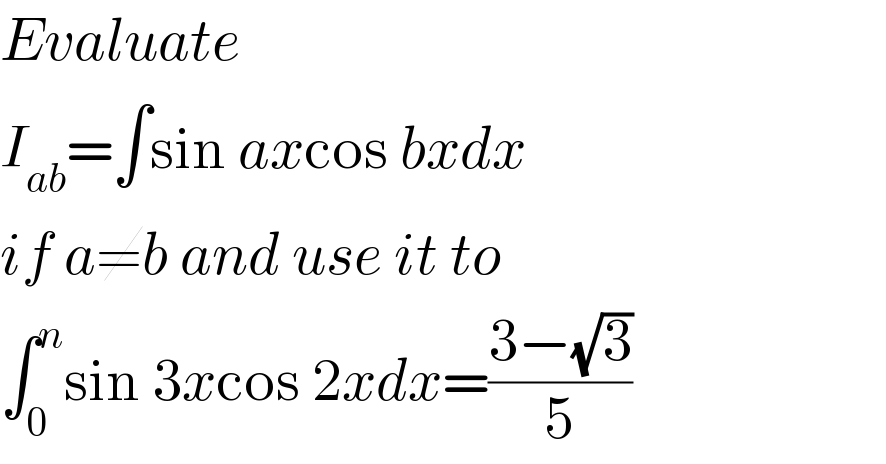
$${Evaluate} \\ $$$${I}_{{ab}} =\int\mathrm{sin}\:{ax}\mathrm{cos}\:{bxdx} \\ $$$${if}\:{a}\neq{b}\:{and}\:{use}\:{it}\:{to} \\ $$$$\int_{\mathrm{0}} ^{{n}} \mathrm{sin}\:\mathrm{3}{x}\mathrm{cos}\:\mathrm{2}{xdx}=\frac{\mathrm{3}−\sqrt{\mathrm{3}}}{\mathrm{5}} \\ $$
Answered by mr W last updated on 01/Jan/20
![sin (ax+bx)=sin ax cos bx+cos ax sin bx sin (ax−bx)=sin ax cos bx−cos ax sin bx ⇒sin ax cos bx=((sin (a+b)x+sin (a−b)x)/2) I=∫sin ax cos bx dx =(1/2)∫(sin (a+b)x+sin (a−b)x)dx =−(1/2)[((cos (a+b)x)/(a+b))+((cos (a−b)x)/(a−b))]+C](Q76969.png)
$$\mathrm{sin}\:\left({ax}+{bx}\right)=\mathrm{sin}\:{ax}\:\mathrm{cos}\:{bx}+\mathrm{cos}\:{ax}\:\mathrm{sin}\:{bx} \\ $$$$\mathrm{sin}\:\left({ax}−{bx}\right)=\mathrm{sin}\:{ax}\:\mathrm{cos}\:{bx}−\mathrm{cos}\:{ax}\:\mathrm{sin}\:{bx} \\ $$$$\Rightarrow\mathrm{sin}\:{ax}\:\mathrm{cos}\:{bx}=\frac{\mathrm{sin}\:\left({a}+{b}\right){x}+\mathrm{sin}\:\left({a}−{b}\right){x}}{\mathrm{2}} \\ $$$${I}=\int\mathrm{sin}\:{ax}\:\mathrm{cos}\:{bx}\:{dx} \\ $$$$=\frac{\mathrm{1}}{\mathrm{2}}\int\left(\mathrm{sin}\:\left({a}+{b}\right){x}+\mathrm{sin}\:\left({a}−{b}\right){x}\right){dx} \\ $$$$=−\frac{\mathrm{1}}{\mathrm{2}}\left[\frac{\mathrm{cos}\:\left({a}+{b}\right){x}}{{a}+{b}}+\frac{\mathrm{cos}\:\left({a}−{b}\right){x}}{{a}−{b}}\right]+{C} \\ $$
Commented by peter frank last updated on 02/Jan/20

$${thank}\:{you} \\ $$
Commented by peter frank last updated on 02/Jan/20
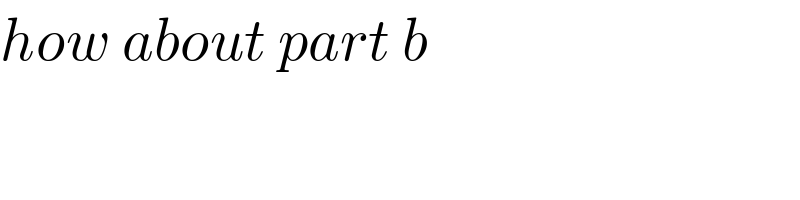
$${how}\:{about}\:{part}\:{b} \\ $$
Commented by mr W last updated on 02/Jan/20
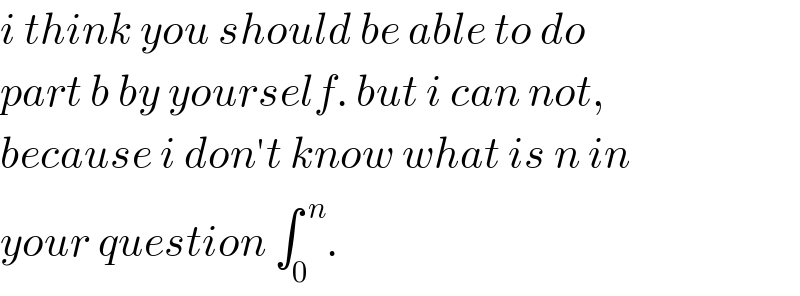
$${i}\:{think}\:{you}\:{should}\:{be}\:{able}\:{to}\:{do} \\ $$$${part}\:{b}\:{by}\:{yourself}.\:{but}\:{i}\:{can}\:{not}, \\ $$$${because}\:{i}\:{don}'{t}\:{know}\:{what}\:{is}\:{n}\:{in} \\ $$$${your}\:{question}\:\int_{\mathrm{0}} ^{\:{n}} . \\ $$
Commented by peter frank last updated on 02/Jan/20

$${thank}\:{you} \\ $$
