Question and Answers Forum

All Questions      Topic List

Limits Questions

Previous in All Question      Next in All Question      

Previous in Limits      Next in Limits      

Question Number 216926 by Engr_Jidda last updated on 24/Feb/25

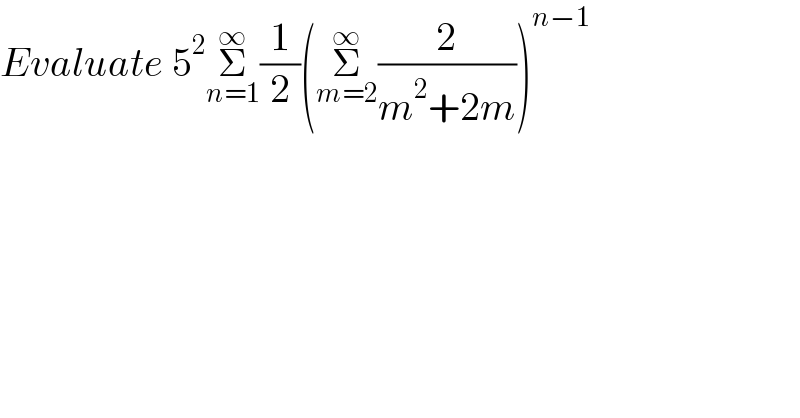
Evaluate 5^2 Σ_(n=1) ^∞ (1/2)(Σ_(m=2) ^∞ (2/(m^2 +2m)))^(n−1)

$${Evaluate}\:\mathrm{5}^{\mathrm{2}} \underset{{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{{m}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{{m}^{\mathrm{2}} +\mathrm{2}{m}}\right)^{{n}−\mathrm{1}} \\ $$

Answered by Wuji last updated on 25/Feb/25

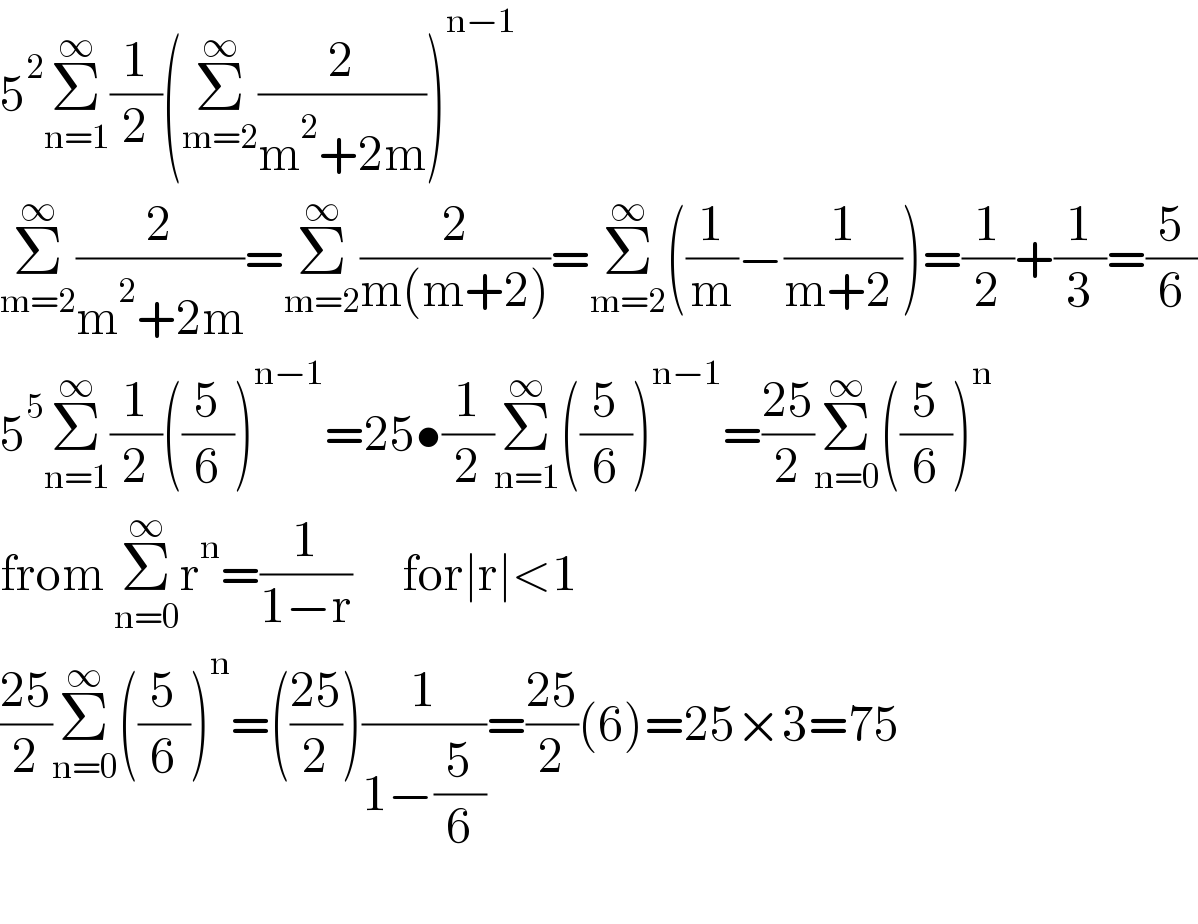
5^2 Σ_(n=1) ^∞ (1/2)(Σ_(m=2) ^∞ (2/(m^2 +2m)))^(n−1) Σ_(m=2) ^∞ (2/(m^2 +2m))=Σ_(m=2) ^∞ (2/(m(m+2)))=Σ_(m=2) ^∞ ((1/m)−(1/(m+2 )))=(1/2)+(1/3)=(5/6) 5^5 Σ_(n=1) ^∞ (1/2)((5/6))^(n−1) =25•(1/2)Σ_(n=1) ^∞ ((5/6))^(n−1) =((25)/2)Σ_(n=0) ^∞ ((5/6))^n from Σ_(n=0) ^∞ r^n =(1/(1−r)) for∣r∣<1 ((25)/2)Σ_(n=0) ^∞ ((5/6))^n =(((25)/2))(1/(1−(5/6)))=((25)/2)(6)=25×3=75

$$\mathrm{5}^{\mathrm{2}} \underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\underset{\mathrm{m}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{m}^{\mathrm{2}} +\mathrm{2m}}\right)^{\mathrm{n}−\mathrm{1}} \\ $$$$\underset{\mathrm{m}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{m}^{\mathrm{2}} +\mathrm{2m}}=\underset{\mathrm{m}=\mathrm{2}} {\overset{\infty} {\sum}}\frac{\mathrm{2}}{\mathrm{m}\left(\mathrm{m}+\mathrm{2}\right)}=\underset{\mathrm{m}=\mathrm{2}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{1}}{\mathrm{m}}−\frac{\mathrm{1}}{\mathrm{m}+\mathrm{2}\:}\right)=\frac{\mathrm{1}}{\mathrm{2}}+\frac{\mathrm{1}}{\mathrm{3}}=\frac{\mathrm{5}}{\mathrm{6}} \\ $$$$\mathrm{5}^{\mathrm{5}} \underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\frac{\mathrm{1}}{\mathrm{2}}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{n}−\mathrm{1}} =\mathrm{25}\bullet\frac{\mathrm{1}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{1}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{n}−\mathrm{1}} =\frac{\mathrm{25}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{n}} \\ $$$$\mathrm{from}\:\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\mathrm{r}^{\mathrm{n}} =\frac{\mathrm{1}}{\mathrm{1}−\mathrm{r}}\:\:\:\:\:\mathrm{for}\mid\mathrm{r}\mid<\mathrm{1} \\ $$$$\frac{\mathrm{25}}{\mathrm{2}}\underset{\mathrm{n}=\mathrm{0}} {\overset{\infty} {\sum}}\left(\frac{\mathrm{5}}{\mathrm{6}}\right)^{\mathrm{n}} =\left(\frac{\mathrm{25}}{\mathrm{2}}\right)\frac{\mathrm{1}}{\mathrm{1}−\frac{\mathrm{5}}{\mathrm{6}}}=\frac{\mathrm{25}}{\mathrm{2}}\left(\mathrm{6}\right)=\mathrm{25}×\mathrm{3}=\mathrm{75} \\ $$$$ \\ $$

Commented by Engr_Jidda last updated on 25/Feb/25

thanks

$${thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com