
Question Number 192452 by Spillover last updated on 18/May/23
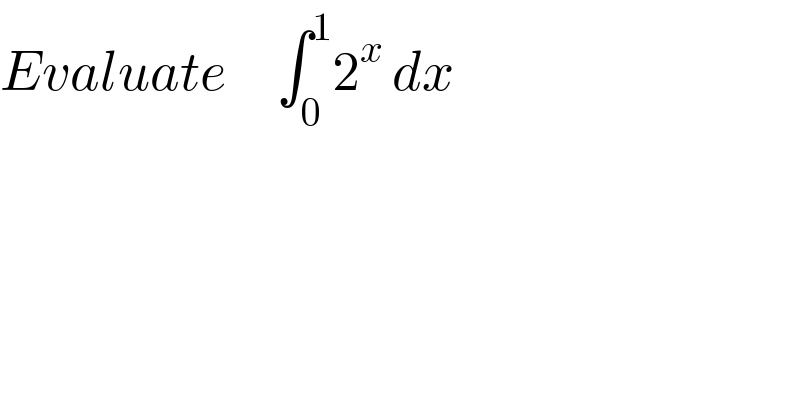
$${Evaluate}\:\:\:\:\:\int_{\mathrm{0}} ^{\mathrm{1}} \mathrm{2}^{{x}\:} {dx}\:\:\: \\ $$$$ \\ $$
Answered by senestro last updated on 18/May/23

$$\mathrm{1}/\mathrm{ln}\:\mathrm{2} \\ $$
Commented by Spillover last updated on 18/May/23
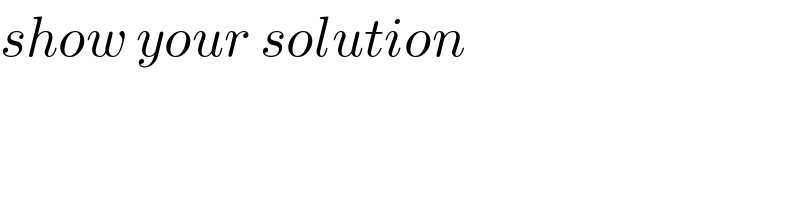
$${show}\:{your}\:{solution} \\ $$
Answered by manxsol last updated on 19/May/23
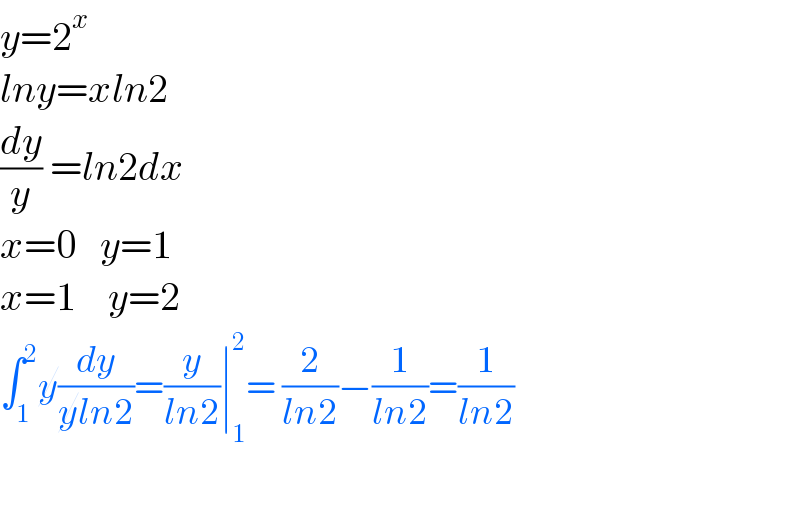
$${y}=\mathrm{2}^{{x}} \\ $$$${lny}={xln}\mathrm{2} \\ $$$$\frac{{dy}}{{y}}\:={ln}\mathrm{2}{dx} \\ $$$${x}=\mathrm{0}\:\:\:{y}=\mathrm{1} \\ $$$${x}=\mathrm{1}\:\:\:\:{y}=\mathrm{2} \\ $$$$\int_{\mathrm{1}} ^{\mathrm{2}} \cancel{{y}}\frac{{dy}}{\cancel{{y}ln}\mathrm{2}}=\frac{{y}}{{ln}\mathrm{2}}\mid_{\mathrm{1}} ^{\mathrm{2}} =\:\frac{\mathrm{2}}{{ln}\mathrm{2}}−\frac{\mathrm{1}}{{ln}\mathrm{2}}=\frac{\mathrm{1}}{{ln}\mathrm{2}} \\ $$$$ \\ $$
