Question and Answers Forum

All Questions      Topic List

Integration Questions

Previous in All Question      Next in All Question      

Previous in Integration      Next in Integration      

Question Number 108954 by mnjuly1970 last updated on 20/Aug/20

Evaluate : Ω=∫_0 ^( 1) ∫_0 ^( 1) (1/(2−x^2 − y^2 )) dxdy=??? ★★♣♣★★

$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\mathscr{E}{valuate}\:: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\Omega=\int_{\mathrm{0}} ^{\:\mathrm{1}} \int_{\mathrm{0}} ^{\:\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}−{x}^{\mathrm{2}} \:−\:{y}^{\mathrm{2}} }\:{dxdy}=???\:\:\: \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\bigstar\bigstar\clubsuit\clubsuit\bigstar\bigstar \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 20/Aug/20

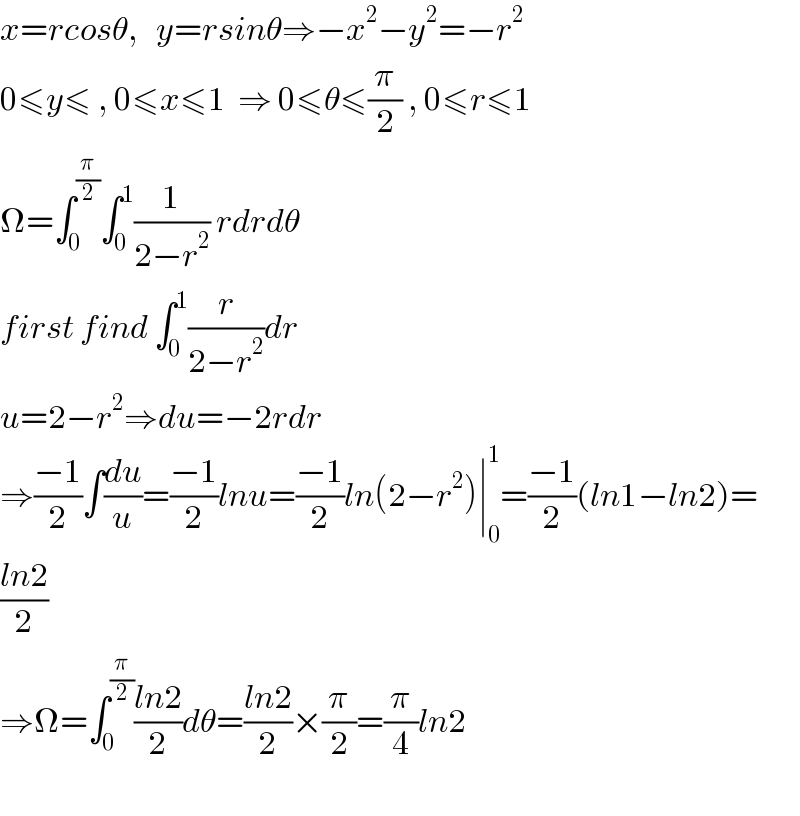
x=rcosθ, y=rsinθ⇒−x^2 −y^2 =−r^2 0≤y≤ , 0≤x≤1 ⇒ 0≤θ≤(π/2) , 0≤r≤1 Ω=∫_0 ^(π/2) ∫_0 ^1 (1/(2−r^2 )) rdrdθ first find ∫_0 ^1 (r/(2−r^2 ))dr u=2−r^2 ⇒du=−2rdr ⇒((−1)/2)∫(du/u)=((−1)/2)lnu=((−1)/2)ln(2−r^2 )∣_0 ^1 =((−1)/2)(ln1−ln2)= ((ln2)/2) ⇒Ω=∫_0 ^(π/2) ((ln2)/2)dθ=((ln2)/2)×(π/2)=(π/4)ln2

$${x}={rcos}\theta,\:\:\:{y}={rsin}\theta\Rightarrow−{x}^{\mathrm{2}} −{y}^{\mathrm{2}} =−{r}^{\mathrm{2}} \\ $$$$\mathrm{0}\leqslant{y}\leqslant\:,\:\mathrm{0}\leqslant{x}\leqslant\mathrm{1}\:\:\Rightarrow\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}\:,\:\mathrm{0}\leqslant{r}\leqslant\mathrm{1} \\ $$$$\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \int_{\mathrm{0}} ^{\mathrm{1}} \frac{\mathrm{1}}{\mathrm{2}−{r}^{\mathrm{2}} }\:{rdrd}\theta \\ $$$${first}\:{find}\:\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{r}}{\mathrm{2}−{r}^{\mathrm{2}} }{dr} \\ $$$${u}=\mathrm{2}−{r}^{\mathrm{2}} \Rightarrow{du}=−\mathrm{2}{rdr} \\ $$$$\Rightarrow\frac{−\mathrm{1}}{\mathrm{2}}\int\frac{{du}}{{u}}=\frac{−\mathrm{1}}{\mathrm{2}}{lnu}=\frac{−\mathrm{1}}{\mathrm{2}}{ln}\left(\mathrm{2}−{r}^{\mathrm{2}} \right)\mid_{\mathrm{0}} ^{\mathrm{1}} =\frac{−\mathrm{1}}{\mathrm{2}}\left({ln}\mathrm{1}−{ln}\mathrm{2}\right)= \\ $$$$\frac{{ln}\mathrm{2}}{\mathrm{2}} \\ $$$$\Rightarrow\Omega=\int_{\mathrm{0}} ^{\frac{\pi}{\mathrm{2}}} \frac{{ln}\mathrm{2}}{\mathrm{2}}{d}\theta=\frac{{ln}\mathrm{2}}{\mathrm{2}}×\frac{\pi}{\mathrm{2}}=\frac{\pi}{\mathrm{4}}{ln}\mathrm{2} \\ $$$$ \\ $$

Commented by mnjuly1970 last updated on 20/Aug/20

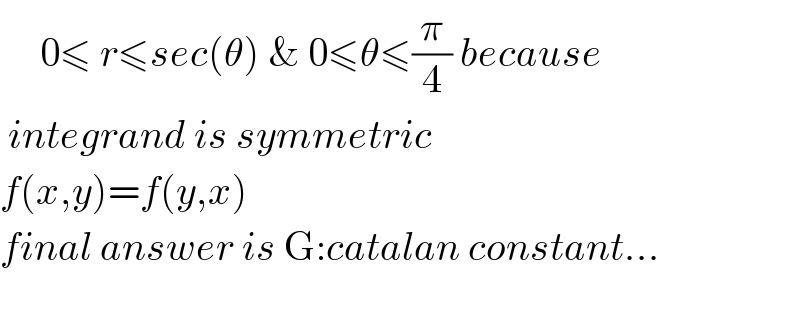
0≤ r≤sec(θ) & 0≤θ≤(π/4) because integrand is symmetric f(x,y)=f(y,x) final answer is G:catalan constant...

$$\:\:\:\:\:\mathrm{0}\leqslant\:{r}\leqslant{sec}\left(\theta\right)\:\&\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{4}}\:{because} \\ $$$$\:{integrand}\:{is}\:{symmetric}\:\: \\ $$$${f}\left({x},{y}\right)={f}\left({y},{x}\right) \\ $$$${final}\:{answer}\:{is}\:\mathrm{G}:{catalan}\:{constant}... \\ $$$$ \\ $$

Commented by kaivan.ahmadi last updated on 20/Aug/20

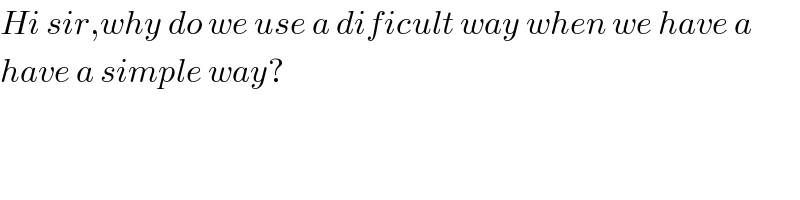
Hi sir,why do we use a dificult way when we have a have a simple way?

$${Hi}\:{sir},{why}\:{do}\:{we}\:{use}\:{a}\:{dificult}\:{way}\:{when}\:{we}\:{have}\:{a} \\ $$$${have}\:{a}\:{simple}\:{way}? \\ $$

Commented by mathmax by abdo last updated on 20/Aug/20

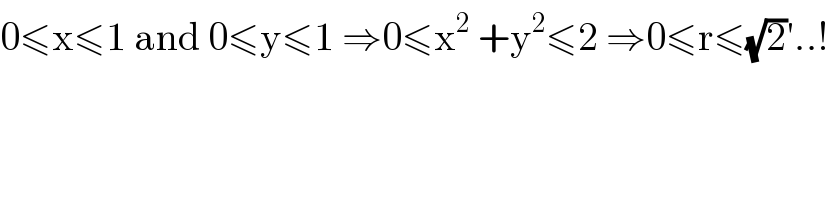
0≤x≤1 and 0≤y≤1 ⇒0≤x^2 +y^2 ≤2 ⇒0≤r≤(√2)′..!

$$\mathrm{0}\leqslant\mathrm{x}\leqslant\mathrm{1}\:\mathrm{and}\:\mathrm{0}\leqslant\mathrm{y}\leqslant\mathrm{1}\:\Rightarrow\mathrm{0}\leqslant\mathrm{x}^{\mathrm{2}} \:+\mathrm{y}^{\mathrm{2}} \leqslant\mathrm{2}\:\Rightarrow\mathrm{0}\leqslant\mathrm{r}\leqslant\sqrt{\mathrm{2}}'..! \\ $$

Commented by kaivan.ahmadi last updated on 21/Aug/20

study polar coordinate system please.

$${study}\:{polar}\:{coordinate}\:{system}\:{please}. \\ $$

Answered by mathmax by abdo last updated on 20/Aug/20

Ω =∫_0 ^1 ∫_0 ^1 ((dxdy)/(2−x^2 −y^2 )) we considere the diffeomorphism { ((x =rcosθ _(⇒ ) Ω =∫∫ _(o≤r≤(√2)and 0≤θ≤(π/2)) (1/(2−r^2 ))r dr dθ)),((y =rsinθ)) :} =(π/2)∫_0 ^(√2) ((rdr)/((2−r^2 ))) =−(π/4) ∫_0 ^(√2) ((−2r)/(2−r^2 ))dr =−(π/4)[ln∣2−r^2 ∣]_0 ^(√2) =∞ this integral is divergent...

$$\Omega\:=\int_{\mathrm{0}} ^{\mathrm{1}} \:\int_{\mathrm{0}} ^{\mathrm{1}} \:\frac{\mathrm{dxdy}}{\mathrm{2}−\mathrm{x}^{\mathrm{2}} −\mathrm{y}^{\mathrm{2}} }\:\:\mathrm{we}\:\mathrm{considere}\:\mathrm{the}\:\mathrm{diffeomorphism} \\ $$$$\begin{cases}{\mathrm{x}\:=\mathrm{rcos}\theta\:\:\:\:\:\:\:\:\:\:\:_{\Rightarrow\:\:} \Omega\:=\int\int\:_{\mathrm{o}\leqslant\mathrm{r}\leqslant\sqrt{\mathrm{2}}\mathrm{and}\:\:\mathrm{0}\leqslant\theta\leqslant\frac{\pi}{\mathrm{2}}} \:\:\:\:\frac{\mathrm{1}}{\mathrm{2}−\mathrm{r}^{\mathrm{2}} }\mathrm{r}\:\mathrm{dr}\:\mathrm{d}\theta}\\{\mathrm{y}\:=\mathrm{rsin}\theta}\end{cases} \\ $$$$=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\frac{\mathrm{rdr}}{\left(\mathrm{2}−\mathrm{r}^{\mathrm{2}} \right)}\:=−\frac{\pi}{\mathrm{4}}\:\int_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:\:\:\frac{−\mathrm{2r}}{\mathrm{2}−\mathrm{r}^{\mathrm{2}} }\mathrm{dr}\:=−\frac{\pi}{\mathrm{4}}\left[\mathrm{ln}\mid\mathrm{2}−\mathrm{r}^{\mathrm{2}} \mid\right]_{\mathrm{0}} ^{\sqrt{\mathrm{2}}} \:=\infty \\ $$$$\mathrm{this}\:\mathrm{integral}\:\mathrm{is}\:\mathrm{divergent}...\:\: \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com