
Question Number 20612 by ajfour last updated on 29/Aug/17
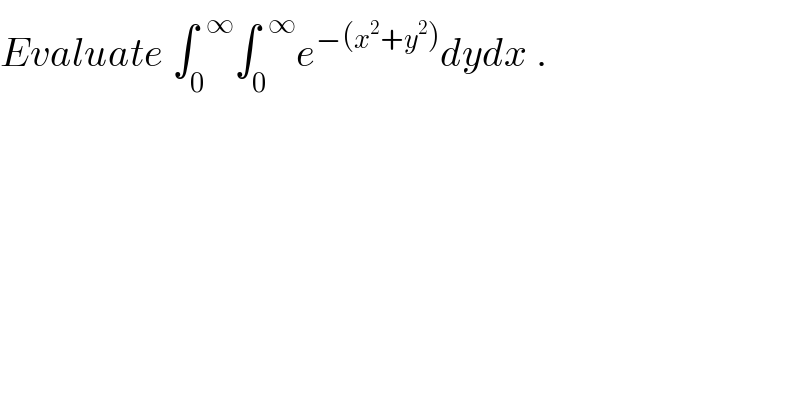
$${Evaluate}\:\int_{\mathrm{0}} ^{\:\:\infty} \int_{\mathrm{0}} ^{\:\:\infty} {e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dydx}\:. \\ $$
Answered by ajfour last updated on 29/Aug/17
![let x^2 +y^2 =r^2 that is x=rcos θ ; y=rsin θ dx=−rsin θdθ ; dy=rcos θdθ ∫_0 ^( ∞) ∫_0 ^( ∞) e^(−(x^2 +y^2 )) dydx =I I=∫_0 ^( ∞) [∫_( 0) ^( π/2) e^(−r^2 ) rdθ]dr =(π/2)∫_0 ^( ∞) e^(−r^2 ) rdr =(π/4)∫_∞ ^( 0) e^(−r^2 ) (−2rdr) I= (π/4)(e^(−r^2 ) )∣_∞ ^0 = (π/4) .](Q20621.png)
$${let}\:\:{x}^{\mathrm{2}} +{y}^{\mathrm{2}} ={r}^{\mathrm{2}} \\ $$$${that}\:{is}\:\:{x}={r}\mathrm{cos}\:\theta\:\:;\:\:{y}={r}\mathrm{sin}\:\theta \\ $$$${dx}=−{r}\mathrm{sin}\:\theta{d}\theta\:\:\:;\:\:{dy}={r}\mathrm{cos}\:\theta{d}\theta \\ $$$$\int_{\mathrm{0}} ^{\:\:\infty} \int_{\mathrm{0}} ^{\:\:\infty} {e}^{−\left({x}^{\mathrm{2}} +{y}^{\mathrm{2}} \right)} {dydx}\:={I} \\ $$$${I}=\int_{\mathrm{0}} ^{\:\:\infty} \left[\int_{\:\mathrm{0}} ^{\:\:\pi/\mathrm{2}} {e}^{−{r}^{\mathrm{2}} } {rd}\theta\right]{dr} \\ $$$$\:\:=\frac{\pi}{\mathrm{2}}\int_{\mathrm{0}} ^{\:\:\infty} {e}^{−{r}^{\mathrm{2}} } {rdr}\:\:=\frac{\pi}{\mathrm{4}}\int_{\infty} ^{\:\:\mathrm{0}} {e}^{−{r}^{\mathrm{2}} } \left(−\mathrm{2}{rdr}\right) \\ $$$${I}=\:\frac{\pi}{\mathrm{4}}\left({e}^{−{r}^{\mathrm{2}} } \right)\mid_{\infty} ^{\mathrm{0}} \:=\:\frac{\pi}{\mathrm{4}}\:. \\ $$$$ \\ $$
