Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 115261 by bobhans last updated on 24/Sep/20

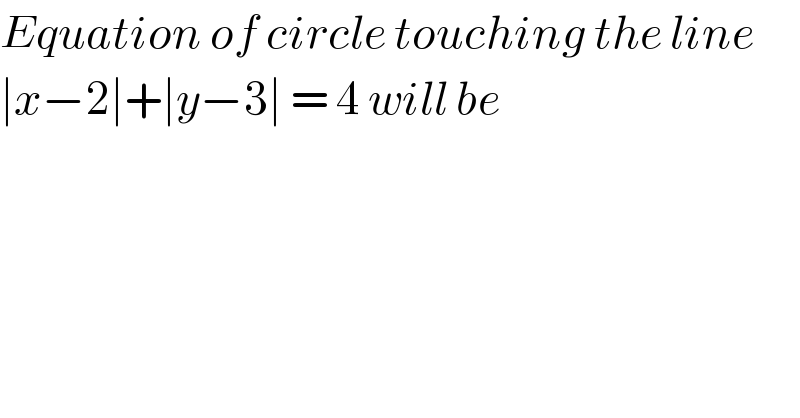
Equation of circle touching the line ∣x−2∣+∣y−3∣ = 4 will be

$${Equation}\:{of}\:{circle}\:{touching}\:{the}\:{line}\: \\ $$$$\mid{x}−\mathrm{2}\mid+\mid{y}−\mathrm{3}\mid\:=\:\mathrm{4}\:{will}\:{be}\: \\ $$

Answered by john santu last updated on 24/Sep/20

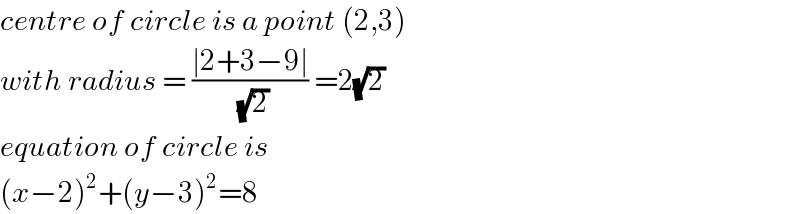
centre of circle is a point (2,3) with radius = ((∣2+3−9∣)/( (√2))) =2(√2) equation of circle is (x−2)^2 +(y−3)^2 =8

$${centre}\:{of}\:{circle}\:{is}\:{a}\:{point}\:\left(\mathrm{2},\mathrm{3}\right) \\ $$$${with}\:{radius}\:=\:\frac{\mid\mathrm{2}+\mathrm{3}−\mathrm{9}\mid}{\:\sqrt{\mathrm{2}}}\:=\mathrm{2}\sqrt{\mathrm{2}} \\ $$$${equation}\:{of}\:{circle}\:{is}\: \\ $$$$\left({x}−\mathrm{2}\right)^{\mathrm{2}} +\left({y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{8} \\ $$

Answered by 1549442205PVT last updated on 24/Sep/20

Graph of the function ∣x−2∣+∣y−3∣=4 consists of four segments that four intersection points are A(−2,3),B(2,7) C(6,3)^� ,D(2,1)⇒ABCD is a square with side equal to 4(√2) ,the center is I(2,3),so the distance from I(2,3) to each of sides equal to the distance from I to line y=−x+9 or x+y−9=0,so R=((∣2+3−9∣)/( (√(1^2 +1^2 ))))=2(√2) .Thus,the equation of the circle touches to the graph is (x−2)^2 +(y−3)^2 =8

$$\mathrm{Graph}\:\mathrm{of}\:\mathrm{the}\:\mathrm{function}\:\mid\mathrm{x}−\mathrm{2}\mid+\mid\mathrm{y}−\mathrm{3}\mid=\mathrm{4} \\ $$$$\mathrm{consists}\:\mathrm{of}\:\mathrm{four}\:\mathrm{segments}\:\mathrm{that}\:\mathrm{four} \\ $$$$\mathrm{intersection}\:\mathrm{points}\:\mathrm{are}\:\mathrm{A}\left(−\mathrm{2},\mathrm{3}\right),\mathrm{B}\left(\mathrm{2},\mathrm{7}\right) \\ $$$$\mathrm{C}\left(\mathrm{6},\mathrm{3}\bar {\right)},\mathrm{D}\left(\mathrm{2},\mathrm{1}\right)\Rightarrow\mathrm{ABCD}\:\mathrm{is}\:\mathrm{a}\:\mathrm{square} \\ $$$$\mathrm{with}\:\mathrm{side}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{4}\sqrt{\mathrm{2}}\:,\mathrm{the}\:\mathrm{center}\:\mathrm{is} \\ $$$$\mathrm{I}\left(\mathrm{2},\mathrm{3}\right),\mathrm{so}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{from}\:\mathrm{I}\left(\mathrm{2},\mathrm{3}\right)\:\mathrm{to} \\ $$$$\mathrm{each}\:\mathrm{of}\:\mathrm{sides}\:\mathrm{equal}\:\mathrm{to}\:\mathrm{the}\:\mathrm{distance}\:\mathrm{from} \\ $$$$\mathrm{I}\:\mathrm{to}\:\mathrm{line}\:\mathrm{y}=−\mathrm{x}+\mathrm{9}\:\mathrm{or}\:\mathrm{x}+\mathrm{y}−\mathrm{9}=\mathrm{0},\mathrm{so} \\ $$$$\mathrm{R}=\frac{\mid\mathrm{2}+\mathrm{3}−\mathrm{9}\mid}{\:\sqrt{\mathrm{1}^{\mathrm{2}} +\mathrm{1}^{\mathrm{2}} }}=\mathrm{2}\sqrt{\mathrm{2}}\:.\mathrm{Thus},\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{of}\:\mathrm{the}\:\mathrm{circle}\:\mathrm{touches}\:\mathrm{to}\:\mathrm{the}\:\:\mathrm{graph}\:\mathrm{is} \\ $$$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{2}} +\left(\mathrm{y}−\mathrm{3}\right)^{\mathrm{2}} =\mathrm{8} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com