Question and Answers Forum

All Questions      Topic List

None Questions

Previous in All Question      Next in All Question      

Previous in None      Next in None      

Question Number 218162 by Ismoiljon_008 last updated on 31/Mar/25

Each edge of a parallelepiped is 1 cm long. At one of its vertices, all three face angles are acute, and each measures 2α. Find the volume of the parallepiped. Help me, please

$$\:\:\: \\ $$$$\:\:\:{Each}\:{edge}\:{of}\:{a}\:{parallelepiped}\:{is}\:\mathrm{1}\:{cm}\:{long}. \\ $$$$\:\:\:{At}\:{one}\:{of}\:{its}\:{vertices},\:{all}\:{three}\:{face}\:{angles} \\ $$$$\:\:\:{are}\:{acute},\:{and}\:{each}\:{measures}\:\mathrm{2}\alpha. \\ $$$$\:\:\:{Find}\:{the}\:{volume}\:{of}\:{the}\:{parallepiped}. \\ $$$$\:\:\:{Help}\:{me},\:\:{please} \\ $$

Answered by mr W last updated on 31/Mar/25

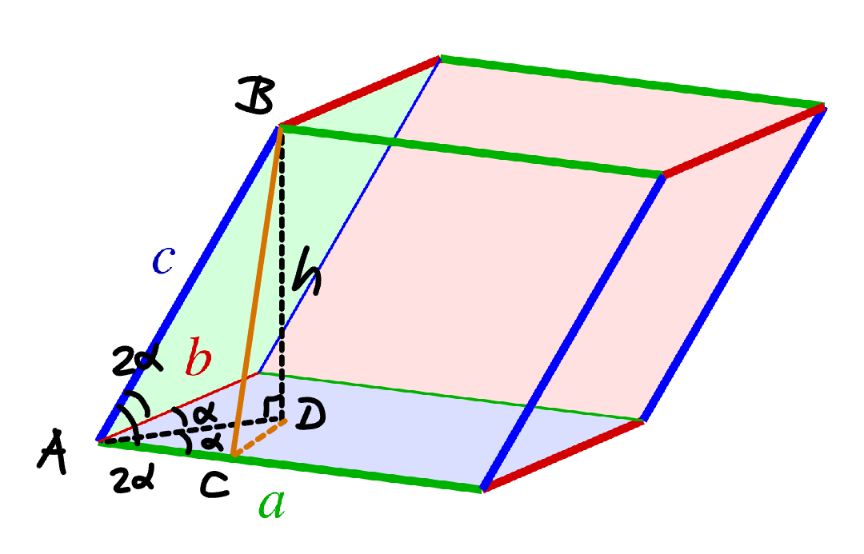
Commented by mr W last updated on 31/Mar/25

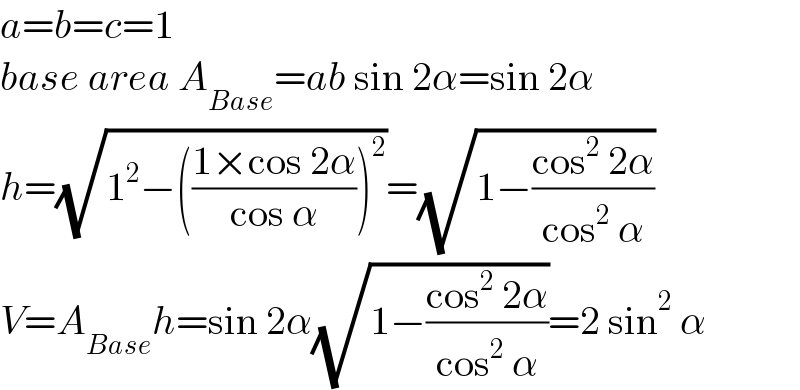
a=b=c=1 base area A_(Base) =ab sin 2α=sin 2α h=(√(1^2 −(((1×cos 2α)/(cos α)))^2 ))=(√(1−((cos^2 2α)/(cos^2 α)))) V=A_(Base) h=sin 2α(√(1−((cos^2 2α)/(cos^2 α))))=2 sin^2 α

$${a}={b}={c}=\mathrm{1} \\ $$$${base}\:{area}\:{A}_{{Base}} ={ab}\:\mathrm{sin}\:\mathrm{2}\alpha=\mathrm{sin}\:\mathrm{2}\alpha \\ $$$${h}=\sqrt{\mathrm{1}^{\mathrm{2}} −\left(\frac{\mathrm{1}×\mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{cos}\:\alpha}\right)^{\mathrm{2}} }=\sqrt{\mathrm{1}−\frac{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\alpha}{\mathrm{cos}^{\mathrm{2}} \:\alpha}} \\ $$$${V}={A}_{{Base}} {h}=\mathrm{sin}\:\mathrm{2}\alpha\sqrt{\mathrm{1}−\frac{\mathrm{cos}^{\mathrm{2}} \:\mathrm{2}\alpha}{\mathrm{cos}^{\mathrm{2}} \:\alpha}}=\mathrm{2}\:\mathrm{sin}^{\mathrm{2}} \:\alpha \\ $$

Commented by Ismoiljon_008 last updated on 31/Mar/25

Thank you very much

$$\:\:\:{Thank}\:{you}\:{very}\:{much} \\ $$

Commented by Ismoiljon_008 last updated on 31/Mar/25

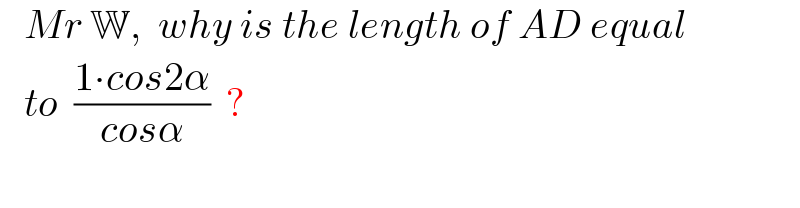
Mr W, why is the length of AD equal to ((1∙cos2α)/(cosα)) ?

$$\:\:\:{Mr}\:\mathbb{W},\:\:{why}\:{is}\:{the}\:{length}\:{of}\:{AD}\:{equal} \\ $$$$\:\:\:{to}\:\:\frac{\mathrm{1}\centerdot{cos}\mathrm{2}\alpha}{{cos}\alpha}\:\:?\: \\ $$$$ \\ $$

Commented by mr W last updated on 31/Mar/25

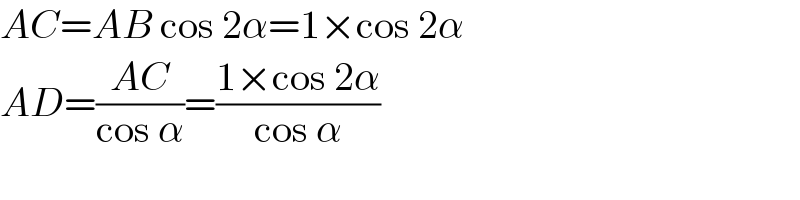
AC=AB cos 2α=1×cos 2α AD=((AC)/(cos α))=((1×cos 2α)/(cos α))

$${AC}={AB}\:\mathrm{cos}\:\mathrm{2}\alpha=\mathrm{1}×\mathrm{cos}\:\mathrm{2}\alpha \\ $$$${AD}=\frac{{AC}}{\mathrm{cos}\:\alpha}=\frac{\mathrm{1}×\mathrm{cos}\:\mathrm{2}\alpha}{\mathrm{cos}\:\alpha} \\ $$

Commented by Ismoiljon_008 last updated on 31/Mar/25

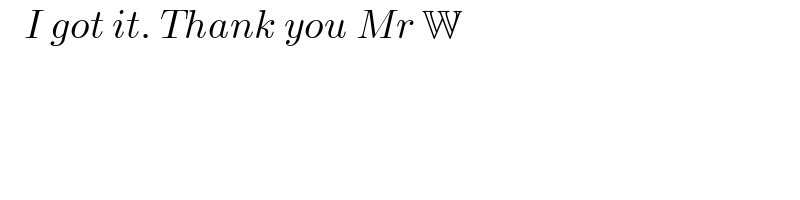
I got it. Thank you Mr W

$$\:\:\:{I}\:{got}\:{it}.\:{Thank}\:{you}\:{Mr}\:\mathbb{W}\: \\ $$$$ \\ $$

Commented by mr W last updated on 31/Mar/25

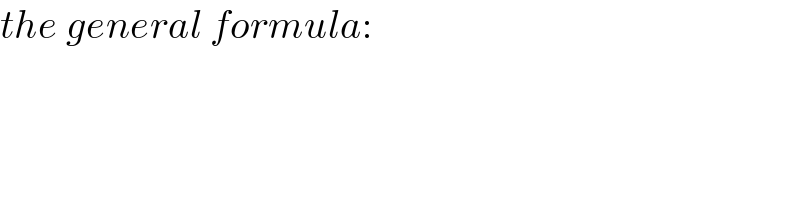
the general formula:

$${the}\:{general}\:{formula}: \\ $$

Commented by mr W last updated on 31/Mar/25

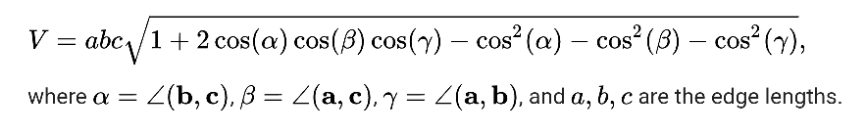
Commented by Ismoiljon_008 last updated on 01/Apr/25

Thanks

$$\:\:\:{Thanks} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com