
Question Number 215951 by alcohol last updated on 22/Jan/25
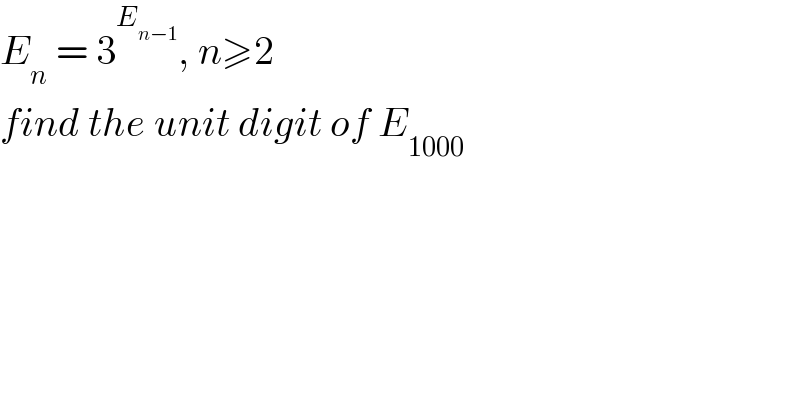
$${E}_{{n}} \:=\:\mathrm{3}^{{E}_{{n}−\mathrm{1}} } ,\:{n}\geqslant\mathrm{2} \\ $$$${find}\:{the}\:{unit}\:{digit}\:{of}\:{E}_{\mathrm{1000}} \\ $$
Answered by A5T last updated on 22/Jan/25
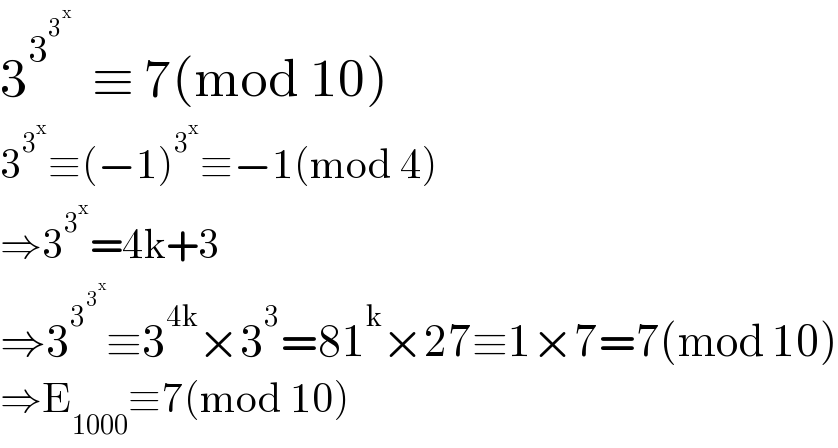
$$\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{\mathrm{x}} } } \:\:\equiv\:\mathrm{7}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\mathrm{3}^{\mathrm{3}^{\mathrm{x}} } \equiv\left(−\mathrm{1}\right)^{\mathrm{3}^{\mathrm{x}} } \equiv−\mathrm{1}\left(\mathrm{mod}\:\mathrm{4}\right) \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{3}^{\mathrm{x}} } =\mathrm{4k}+\mathrm{3} \\ $$$$\Rightarrow\mathrm{3}^{\mathrm{3}^{\mathrm{3}^{\mathrm{x}} } } \equiv\mathrm{3}^{\mathrm{4k}} ×\mathrm{3}^{\mathrm{3}} =\mathrm{81}^{\mathrm{k}} ×\mathrm{27}\equiv\mathrm{1}×\mathrm{7}=\mathrm{7}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$$$\Rightarrow\mathrm{E}_{\mathrm{1000}} \equiv\mathrm{7}\left(\mathrm{mod}\:\mathrm{10}\right) \\ $$
