
Question Number 206007 by SANOGO last updated on 04/Apr/24
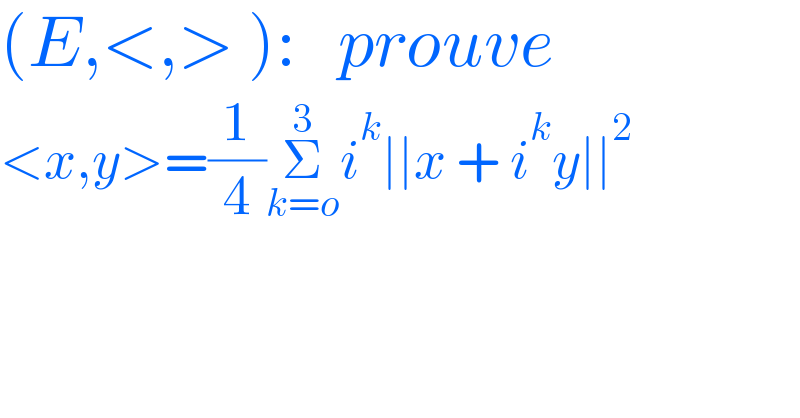
$$\left({E},<,>\:\right):\:\:\:{prouve} \\ $$$$<{x},{y}>=\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}={o}} {\overset{\mathrm{3}} {\sum}}{i}^{{k}} \mid\mid{x}\:+\:{i}^{{k}} {y}\mid\mid^{\mathrm{2}} \\ $$
Commented by Berbere last updated on 04/Apr/24
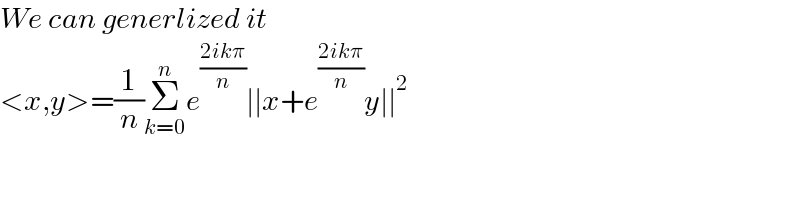
$${We}\:{can}\:{generlized}\:{it} \\ $$$$<{x},{y}>=\frac{\mathrm{1}}{{n}}\underset{{k}=\mathrm{0}} {\overset{{n}} {\sum}}{e}^{\frac{\mathrm{2}{ik}\pi}{{n}}} \mid\mid{x}+{e}^{\frac{\mathrm{2}{ik}\pi}{{n}}} {y}\mid\mid^{\mathrm{2}} \\ $$
Answered by Berbere last updated on 04/Apr/24
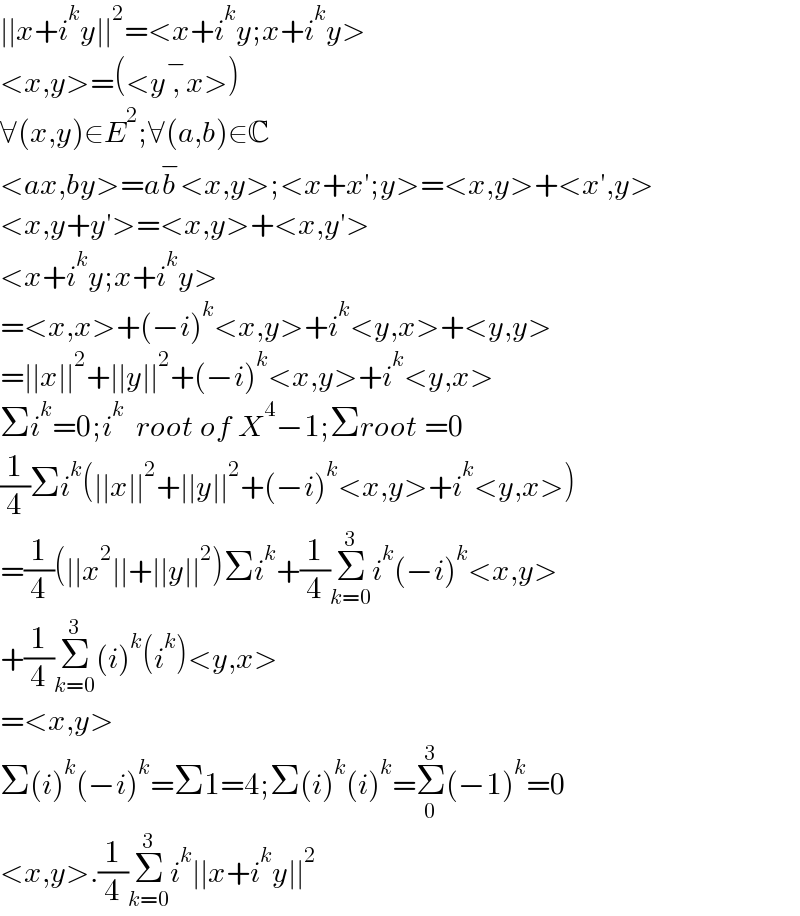
$$\mid\mid{x}+{i}^{{k}} {y}\mid\mid^{\mathrm{2}} =<{x}+{i}^{{k}} {y};{x}+{i}^{{k}} {y}> \\ $$$$<{x},{y}>=\left(<{y}\overset{−} {,}{x}>\right) \\ $$$$\forall\left({x},{y}\right)\in{E}^{\mathrm{2}} ;\forall\left({a},{b}\right)\in\mathbb{C} \\ $$$$<{ax},{by}>={a}\overset{−} {{b}}<{x},{y}>;<{x}+{x}';{y}>=<{x},{y}>+<{x}',{y}> \\ $$$$<{x},{y}+{y}'>=<{x},{y}>+<{x},{y}'> \\ $$$$<{x}+{i}^{{k}} {y};{x}+{i}^{{k}} {y}> \\ $$$$=<{x},{x}>+\left(−{i}\right)^{{k}} <{x},{y}>+{i}^{{k}} <{y},{x}>+<{y},{y}> \\ $$$$=\mid\mid{x}\mid\mid^{\mathrm{2}} +\mid\mid{y}\mid\mid^{\mathrm{2}} +\left(−{i}\right)^{{k}} <{x},{y}>+{i}^{{k}} <{y},{x}> \\ $$$$\Sigma{i}^{{k}} =\mathrm{0};{i}^{{k}} \:\:{root}\:{of}\:{X}^{\mathrm{4}} −\mathrm{1};\Sigma{root}\:=\mathrm{0} \\ $$$$\frac{\mathrm{1}}{\mathrm{4}}\Sigma{i}^{{k}} \left(\mid\mid{x}\mid\mid^{\mathrm{2}} +\mid\mid{y}\mid\mid^{\mathrm{2}} +\left(−{i}\right)^{{k}} <{x},{y}>+{i}^{{k}} <{y},{x}>\right) \\ $$$$=\frac{\mathrm{1}}{\mathrm{4}}\left(\mid\mid{x}^{\mathrm{2}} \mid\mid+\mid\mid{y}\mid\mid^{\mathrm{2}} \right)\Sigma{i}^{{k}} +\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}{i}^{{k}} \left(−{i}\right)^{{k}} <{x},{y}> \\ $$$$+\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\left({i}\right)^{{k}} \left({i}^{{k}} \right)<{y},{x}> \\ $$$$=<{x},{y}> \\ $$$$\Sigma\left({i}\right)^{{k}} \left(−{i}\right)^{{k}} =\Sigma\mathrm{1}=\mathrm{4};\Sigma\left({i}\right)^{{k}} \left({i}\right)^{{k}} =\underset{\mathrm{0}} {\overset{\mathrm{3}} {\sum}}\left(−\mathrm{1}\right)^{{k}} =\mathrm{0} \\ $$$$<{x},{y}>.\frac{\mathrm{1}}{\mathrm{4}}\underset{{k}=\mathrm{0}} {\overset{\mathrm{3}} {\sum}}{i}^{{k}} \mid\mid{x}+{i}^{{k}} {y}\mid\mid^{\mathrm{2}} \\ $$
