
Question Number 206339 by mnjuly1970 last updated on 12/Apr/24
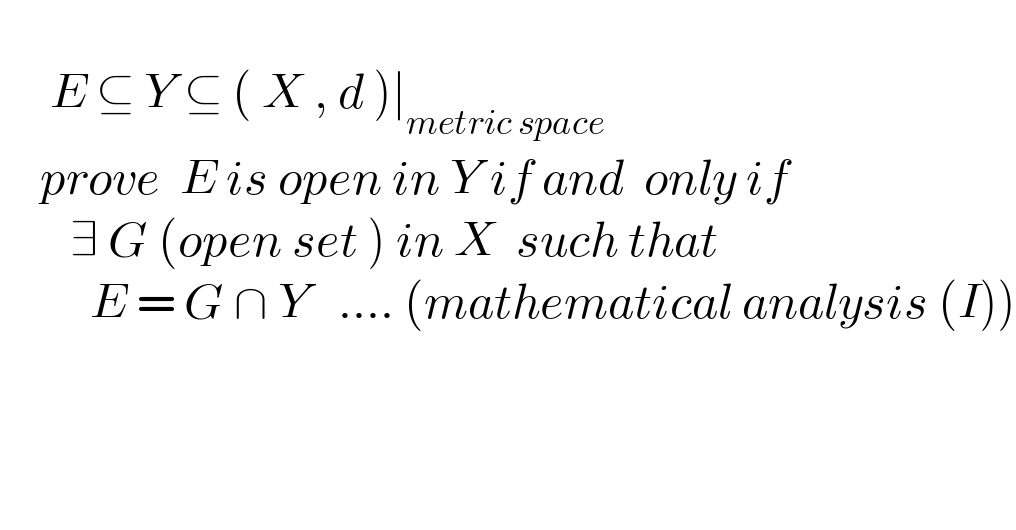
$$ \\ $$$$\:\:\:\:\:{E}\:\subseteq\:{Y}\:\subseteq\:\left(\:{X}\:,\:{d}\:\right)\mid_{{metric}\:{space}} \\ $$$$\:\:\:\:{prove}\:\:{E}\:{is}\:{open}\:{in}\:{Y}\:{if}\:{and}\:\:{only}\:{if} \\ $$$$\:\:\:\:\:\:\:\exists\:{G}\:\left({open}\:{set}\:\right)\:{in}\:{X}\:\:{such}\:{that} \\ $$$$\:\:\:\:\:\:\:\:\:{E}\:=\:{G}\:\cap\:{Y}\:\:\:....\:\left({mathematical}\:{analysis}\:\left({I}\right)\right) \\ $$
Answered by Berbere last updated on 13/Apr/24

$${E}={G}\cap{Y}\:\:{G}\:{let}\:{a}\in{E};{a}\in{G}\:{since}\:{G}\:{is}\:{open}\:{in}\:{X} \\ $$$$\exists\:{O}\in{X}\:{opene}\:{such}\:{that}\:{a}\in{O}\:\subset{G}\: \\ $$$${O}\cap{Y}\:{is}\:{open}\:{in}\:{Y}\:{since}\:{Y}\:{sub}\left[{space}\:{of}\:\left({X},{d}\right)\:{induit}\:{Topolopgiep}\right. \\ $$$$\left({O}\cap{Y}\right)\subset\left({G}\cap{Y}\right)={E}\:{open}\:{in}\:{Y}\: \\ $$$${Suppose}\:{E}\:{is}\:{opened}\:{in}\:{Y} \\ $$$${E}=\underset{{e}\in{E}} {\cup}\left\{{e}\right\}\:\: \\ $$$$\forall{e}\:\exists\:{O}_{{e}} \:{open}\:{in}\:{Y}\:{such}\:{That}\:{e}\in{O}_{{e}} \subset{E} \\ $$$${O}_{{e}} ={O}_{{e}} '\cap{Y}\:,{O}'_{{e}} \:{open}\:{in}\:{X} \\ $$$${G}=\cup_{{e}} {O}'_{{e}} \:{opene}\:{in}\:\left({X},{d}\right) \\ $$$$\forall{e}\:\:{O}'_{{e}} \:\cap{Y}\:={O}_{{e}} \:{open}\:{in}\:{Y} \\ $$$${G}\:\cap{Y}\:{is}\:{open}\:{in}\:{Y}\:\Rightarrow{G}=\underset{{e}\in{E}} {\cup}{O}'_{{e}} \:{worcks} \\ $$
