
Question Number 209308 by Erico last updated on 06/Jul/24
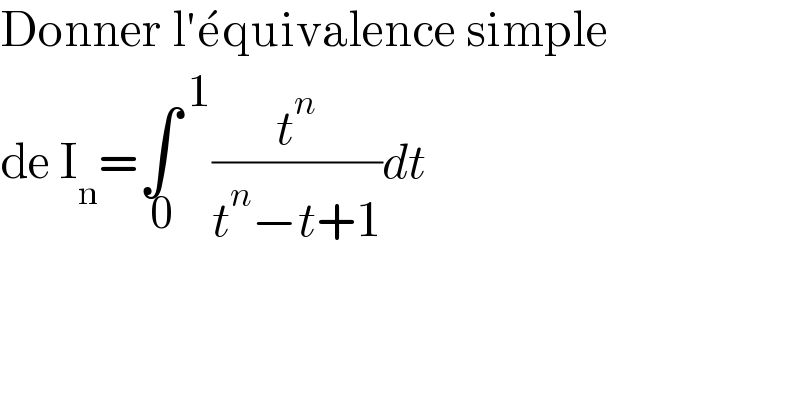
$$\mathrm{Donner}\:\mathrm{l}'\acute {\mathrm{e}quivalence}\:\mathrm{simple} \\ $$$$\mathrm{de}\:\mathrm{I}_{\mathrm{n}} =\underset{\:\mathrm{0}} {\int}^{\:\mathrm{1}} \frac{{t}^{{n}} }{{t}^{{n}} −{t}+\mathrm{1}}{dt} \\ $$
Answered by mathzup last updated on 07/Jul/24
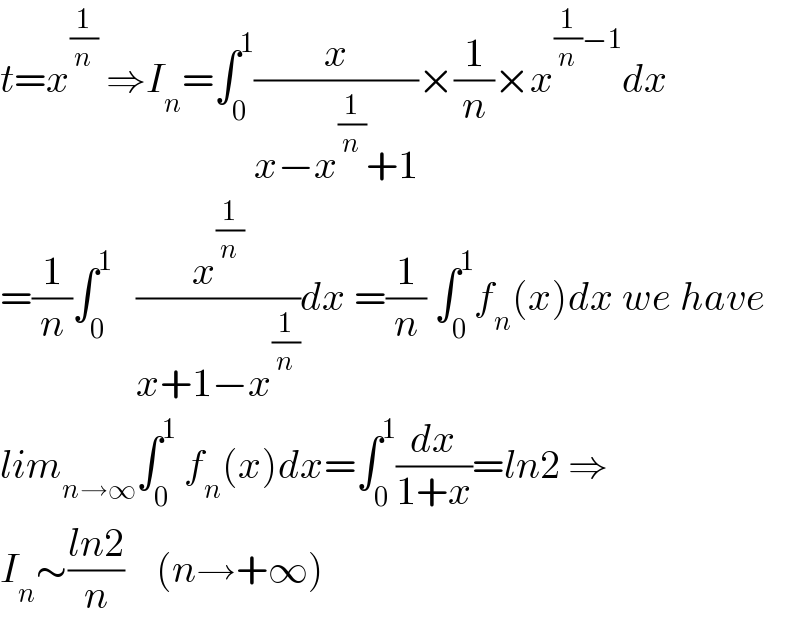
$${t}={x}^{\frac{\mathrm{1}}{{n}}} \:\Rightarrow{I}_{{n}} =\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{x}}{{x}−{x}^{\frac{\mathrm{1}}{{n}}} +\mathrm{1}}×\frac{\mathrm{1}}{{n}}×{x}^{\frac{\mathrm{1}}{{n}}−\mathrm{1}} {dx} \\ $$$$=\frac{\mathrm{1}}{{n}}\int_{\mathrm{0}} ^{\mathrm{1}} \:\:\:\frac{{x}^{\frac{\mathrm{1}}{{n}}} }{{x}+\mathrm{1}−{x}^{\frac{\mathrm{1}}{{n}}} }{dx}\:=\frac{\mathrm{1}}{{n}}\:\int_{\mathrm{0}} ^{\mathrm{1}} {f}_{{n}} \left({x}\right){dx}\:{we}\:{have} \\ $$$${lim}_{{n}\rightarrow\infty} \int_{\mathrm{0}} ^{\mathrm{1}} \:{f}_{{n}} \left({x}\right){dx}=\int_{\mathrm{0}} ^{\mathrm{1}} \frac{{dx}}{\mathrm{1}+{x}}={ln}\mathrm{2}\:\Rightarrow \\ $$$${I}_{{n}} \sim\frac{{ln}\mathrm{2}}{{n}}\:\:\:\:\left({n}\rightarrow+\infty\right) \\ $$
