Question and Answers Forum

All Questions Topic List

DifferentiationQuestion and Answers: Page 63

Question Number 19085 Answers: 0 Comments: 0

f_n (x)=(√(f_(n−1) (x)×(f_(n−1) (x))′)) f_1 (x)=x^(2017) +x^8 +x^4 lim_(n→∞) f_n (x)=?

$$\mathrm{f}_{\mathrm{n}} \left(\mathrm{x}\right)=\sqrt{\mathrm{f}_{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}\right)×\left(\mathrm{f}_{\mathrm{n}−\mathrm{1}} \left(\mathrm{x}\right)\right)'} \\ $$$$\mathrm{f}_{\mathrm{1}} \left(\mathrm{x}\right)=\mathrm{x}^{\mathrm{2017}} +\mathrm{x}^{\mathrm{8}} +\mathrm{x}^{\mathrm{4}} \\ $$$$\underset{\mathrm{n}\rightarrow\infty} {\mathrm{lim}f}_{\mathrm{n}} \left(\mathrm{x}\right)=? \\ $$

Question Number 18906 Answers: 1 Comments: 0

calculate (dy/dx) where y=cos^(−1) ((a+b cosx)/(b+a cosx)) (b>a)

$$\mathrm{calculate}\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\:\:\mathrm{where}\: \\ $$$$\mathrm{y}=\mathrm{cos}^{−\mathrm{1}} \frac{\mathrm{a}+\mathrm{b}\:\mathrm{cosx}}{\mathrm{b}+\mathrm{a}\:\mathrm{cosx}}\:\left(\mathrm{b}>\mathrm{a}\right) \\ $$

Question Number 18905 Answers: 0 Comments: 0

prove that the differentiation of(((√(1+x^2 ))−(√(1−x^2 )))/((√(1+x^2 ))+(√(1−x^2 )))) with respect to (√(1−x^4 )) is ((√(1−x^4 ))/x^6 )

$$\mathrm{prove}\:\mathrm{that}\:\mathrm{the}\:\mathrm{differentiation} \\ $$$$\mathrm{of}\frac{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }−\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}{\sqrt{\mathrm{1}+\mathrm{x}^{\mathrm{2}} }+\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{2}} }}\:\:\mathrm{with}\:\mathrm{respect} \\ $$$$\mathrm{to}\:\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }\:\:\mathrm{is}\:\:\frac{\sqrt{\mathrm{1}−\mathrm{x}^{\mathrm{4}} }}{\mathrm{x}^{\mathrm{6}} } \\ $$

Question Number 18446 Answers: 0 Comments: 0

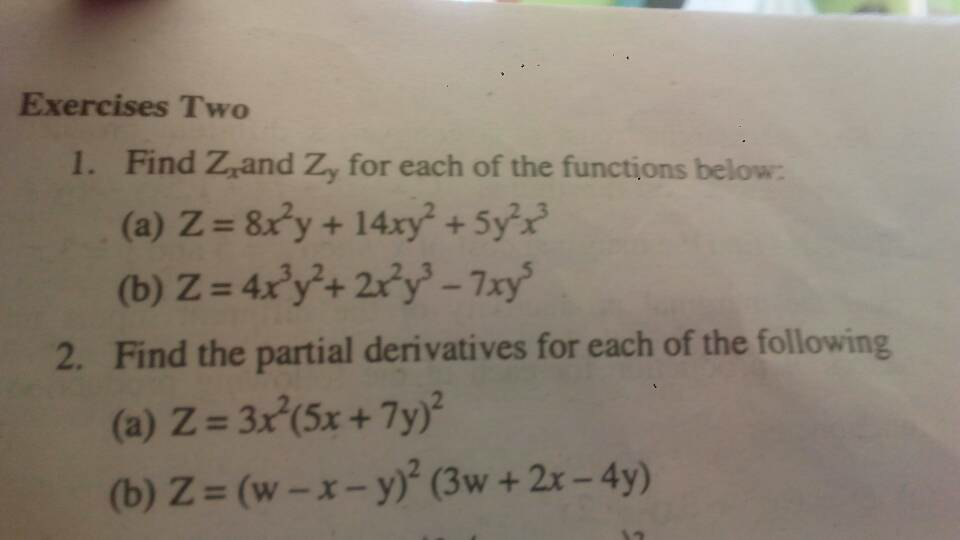
Question Number 18469 Answers: 1 Comments: 0

Find Z_x and Z_y for each of the functions below (a) Z = 8x^2 y + 14xy^2 + 5y^2 x^3 (b) Z = 4x^3 y^2 + 2x^2 y^3 − 7xy^5

$$\mathrm{Find}\:\mathrm{Z}_{\mathrm{x}} \:\mathrm{and}\:\mathrm{Z}_{\mathrm{y}} \:\mathrm{for}\:\mathrm{each}\:\mathrm{of}\:\mathrm{the}\:\mathrm{functions}\:\mathrm{below} \\ $$$$\left(\mathrm{a}\right)\:\:\mathrm{Z}\:=\:\mathrm{8x}^{\mathrm{2}} \mathrm{y}\:+\:\mathrm{14xy}^{\mathrm{2}} \:+\:\mathrm{5y}^{\mathrm{2}} \mathrm{x}^{\mathrm{3}} \\ $$$$\left(\mathrm{b}\right)\:\:\mathrm{Z}\:=\:\mathrm{4x}^{\mathrm{3}} \mathrm{y}^{\mathrm{2}} \:+\:\mathrm{2x}^{\mathrm{2}} \mathrm{y}^{\mathrm{3}} \:−\:\mathrm{7xy}^{\mathrm{5}} \\ $$

Question Number 18470 Answers: 1 Comments: 0

Find the partial derivatives for each of the following (a) Z = 3x^2 (5x + 7y)^2 (b) Z = (w − x − y)^2 (3w + 2x − 4y)

$$\mathrm{Find}\:\mathrm{the}\:\mathrm{partial}\:\mathrm{derivatives}\:\mathrm{for}\:\mathrm{each}\:\mathrm{of}\:\mathrm{the}\:\mathrm{following} \\ $$$$\left(\mathrm{a}\right)\:\mathrm{Z}\:=\:\mathrm{3x}^{\mathrm{2}} \left(\mathrm{5x}\:+\:\mathrm{7y}\right)^{\mathrm{2}} \\ $$$$\left(\mathrm{b}\right)\:\mathrm{Z}\:=\:\left(\mathrm{w}\:−\:\mathrm{x}\:−\:\mathrm{y}\right)^{\mathrm{2}} \:\left(\mathrm{3w}\:+\:\mathrm{2x}\:−\:\mathrm{4y}\right) \\ $$

Question Number 18283 Answers: 0 Comments: 0

Given: x^2 + y^2 Show that, (d^2 y/dx^2 ) = ((xy)/(y^2 + x^2 ))

$$\mathrm{Given}:\:\:\mathrm{x}^{\mathrm{2}} \:+\:\mathrm{y}^{\mathrm{2}} \\ $$$$\mathrm{Show}\:\mathrm{that},\:\:\:\frac{\mathrm{d}^{\mathrm{2}} \mathrm{y}}{\mathrm{dx}^{\mathrm{2}} }\:=\:\frac{\mathrm{xy}}{\mathrm{y}^{\mathrm{2}} \:+\:\mathrm{x}^{\mathrm{2}} } \\ $$

Question Number 17634 Answers: 1 Comments: 0

y = x! , Find y′

$$\mathrm{y}\:=\:\mathrm{x}!\:\:,\:\:\:\:\:\mathrm{Find}\:\:\:\mathrm{y}' \\ $$

Question Number 16893 Answers: 0 Comments: 4

if y=u^n show that d^n y/dx^n =n!

$$\mathrm{if}\:\mathrm{y}=\mathrm{u}^{\mathrm{n}} \:\:\:\mathrm{show}\:\mathrm{that}\:\mathrm{d}^{\mathrm{n}} \mathrm{y}/\mathrm{dx}^{\mathrm{n}} =\mathrm{n}! \\ $$

Question Number 16788 Answers: 0 Comments: 1

Question Number 16689 Answers: 1 Comments: 0

why any infinitely differentiable function is a power series?

$${why}\:{any}\:{infinitely}\:{differentiable}\:{function}\:{is}\:{a}\:{power}\:{series}? \\ $$

Question Number 15797 Answers: 1 Comments: 1

If (a + bx)e^(y/x) = x, where a and b are constant, prove that,: x^3 y′′ = (xy′ − y)^2

$$\mathrm{If}\:\:\left(\mathrm{a}\:+\:\mathrm{bx}\right)\mathrm{e}^{\mathrm{y}/\mathrm{x}} \:=\:\mathrm{x},\:\:\:\mathrm{where}\:\:\mathrm{a}\:\mathrm{and}\:\mathrm{b}\:\mathrm{are}\:\mathrm{constant},\: \\ $$$$\mathrm{prove}\:\mathrm{that},:\:\:\:\mathrm{x}^{\mathrm{3}} \mathrm{y}''\:=\:\left(\mathrm{xy}'\:−\:\mathrm{y}\right)^{\mathrm{2}} \\ $$

Question Number 15741 Answers: 1 Comments: 0

Find the minimum value of x^2 +y^2 +z^2 , with the condition ax+by+cz=p .

$${Find}\:{the}\:{minimum}\:{value}\:\:{of} \\ $$$$\:\:\boldsymbol{{x}}^{\mathrm{2}} +\boldsymbol{{y}}^{\mathrm{2}} +\boldsymbol{{z}}^{\mathrm{2}} ,\:{with}\:{the}\:{condition} \\ $$$$\:{ax}+{by}+{cz}={p}\:. \\ $$

Question Number 15179 Answers: 1 Comments: 0

If (d^2 y/dx^2 ) + 4y = 0 y(0) = 1 and y((π/6)) = ((√3)/2) + (1/2) How to find y(x) ?

$$\mathrm{If}\:\:\frac{{d}^{\mathrm{2}} {y}}{{dx}^{\mathrm{2}} }\:+\:\mathrm{4}{y}\:=\:\mathrm{0}\: \\ $$$${y}\left(\mathrm{0}\right)\:=\:\mathrm{1}\:\mathrm{and}\:{y}\left(\frac{\pi}{\mathrm{6}}\right)\:=\:\frac{\sqrt{\mathrm{3}}}{\mathrm{2}}\:+\:\frac{\mathrm{1}}{\mathrm{2}} \\ $$$$\mathrm{How}\:\mathrm{to}\:\mathrm{find}\:{y}\left({x}\right)\:? \\ $$

Question Number 14513 Answers: 2 Comments: 0

If y^2 (1 + x^2 ) = 1 − x^2 Show that, ((dy/dx))^2 = ((1 − y^4 )/(1 − x^4 ))

$$\mathrm{If}\:\:\mathrm{y}^{\mathrm{2}} \left(\mathrm{1}\:+\:\mathrm{x}^{\mathrm{2}} \right)\:=\:\mathrm{1}\:−\:\mathrm{x}^{\mathrm{2}} \\ $$$$\mathrm{Show}\:\mathrm{that},\:\:\:\left(\frac{\mathrm{dy}}{\mathrm{dx}}\right)^{\mathrm{2}} \:=\:\frac{\mathrm{1}\:−\:\mathrm{y}^{\mathrm{4}} }{\mathrm{1}\:−\:\mathrm{x}^{\mathrm{4}} } \\ $$

Question Number 13955 Answers: 0 Comments: 2

y(x)= { ((4+6x−3x^2 ; x < 2)),((2x^2 −14x+20 ; x ≥ 2)) :} Is the function y(x) differentiable with respect to x at x=2 ?

$${y}\left({x}\right)=\begin{cases}{\mathrm{4}+\mathrm{6}{x}−\mathrm{3}{x}^{\mathrm{2}} \:\:\:\:\:\:\:;\:\:{x}\:<\:\mathrm{2}}\\{\mathrm{2}{x}^{\mathrm{2}} −\mathrm{14}{x}+\mathrm{20}\:\:;\:\:{x}\:\geqslant\:\mathrm{2}}\end{cases} \\ $$$${Is}\:{the}\:{function}\:{y}\left({x}\right)\: \\ $$$${differentiable}\:{with}\:{respect}\:{to}\:{x} \\ $$$${at}\:{x}=\mathrm{2}\:? \\ $$

Question Number 13871 Answers: 0 Comments: 0

why the function,sin(x) is a power series??

$${why}\:{the}\:{function},{sin}\left({x}\right)\:{is}\:{a}\:{power} \\ $$$${series}?? \\ $$

Question Number 13806 Answers: 0 Comments: 1

Prove that for −(π/2)<x<(π/2) , (1/1^3 )cos x−(1/3^3 )cos 3x+(1/5^3 )cos 5x−....to infinity =(π/8)((π^2 /4)−x^2 ) .

$${Prove}\:{that}\:{for}\:−\frac{\pi}{\mathrm{2}}<{x}<\frac{\pi}{\mathrm{2}}\:, \\ $$$$\frac{\mathrm{1}}{\mathrm{1}^{\mathrm{3}} }\mathrm{cos}\:{x}−\frac{\mathrm{1}}{\mathrm{3}^{\mathrm{3}} }\mathrm{cos}\:\mathrm{3}{x}+\frac{\mathrm{1}}{\mathrm{5}^{\mathrm{3}} }\mathrm{cos}\:\mathrm{5}{x}−....{to}\:{infinity} \\ $$$$\:\:=\frac{\pi}{\mathrm{8}}\left(\frac{\pi^{\mathrm{2}} }{\mathrm{4}}−{x}^{\mathrm{2}} \right)\:. \\ $$

Question Number 13751 Answers: 1 Comments: 4

(ds/dt)=v,(dv/dt)=a,(da/dt)=b,(db/dt)=e,(de/dt)=f (df/dt)=g,(dg/dt)=h,(dh/dt)=i,(di/dt)=j,(dj/dt)=k,..... now if we continue this process to infinity..and if v_0 ,v,a,b,e,f,g,h,i, j,................=1 .then calculate the formula of v and s ...

$$\frac{{ds}}{{dt}}={v},\frac{{dv}}{{dt}}={a},\frac{{da}}{{dt}}={b},\frac{{db}}{{dt}}={e},\frac{{de}}{{dt}}={f} \\ $$$$\frac{{df}}{{dt}}={g},\frac{{dg}}{{dt}}={h},\frac{{dh}}{{dt}}={i},\frac{{di}}{{dt}}={j},\frac{{dj}}{{dt}}={k},..... \\ $$$${now}\:{if}\:{we}\:{continue}\:{this}\:{process}\:{to} \\ $$$${infinity}..{and}\:{if}\:{v}_{\mathrm{0}} ,{v},{a},{b},{e},{f},{g},{h},{i}, \\ $$$${j},................=\mathrm{1}\:.{then}\:{calculate} \\ $$$${the}\:{formula}\:{of}\:{v}\:{and}\:{s}\:... \\ $$$$ \\ $$

Question Number 13429 Answers: 0 Comments: 2

Question Number 13427 Answers: 0 Comments: 0

Question Number 13226 Answers: 2 Comments: 0

if x^3 +y^3 =3axy,find dy/dx in terms of x and y and prove that dy/dx cannot be equal to -1 for finite values of x and y except x=y. please help

$$\mathrm{if}\:\mathrm{x}^{\mathrm{3}} +\mathrm{y}^{\mathrm{3}} =\mathrm{3axy},\mathrm{find}\:\mathrm{dy}/\mathrm{dx}\:\mathrm{in}\:\mathrm{terms} \\ $$$$\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{and}\:\mathrm{prove}\:\mathrm{that}\:\mathrm{dy}/\mathrm{dx}\: \\ $$$$\mathrm{cannot}\:\mathrm{be}\:\mathrm{equal}\:\mathrm{to}\:-\mathrm{1}\:\mathrm{for}\:\mathrm{finite} \\ $$$$\mathrm{values}\:\mathrm{of}\:\mathrm{x}\:\mathrm{and}\:\mathrm{y}\:\mathrm{except}\:\mathrm{x}=\mathrm{y}. \\ $$$$ \\ $$$$ \\ $$$$\mathrm{please}\:\mathrm{help}\: \\ $$

Question Number 13068 Answers: 2 Comments: 0

If y = (x)^(1/3) Find (dy/dx) from the first principle

$$\mathrm{If}\:\:\:\mathrm{y}\:=\:\:\sqrt[{\mathrm{3}}]{\mathrm{x}}\:\:\:\:\:\mathrm{Find}\:\:\frac{\mathrm{dy}}{\mathrm{dx}}\:\:\mathrm{from}\:\mathrm{the}\:\mathrm{first}\:\mathrm{principle} \\ $$

Question Number 12968 Answers: 1 Comments: 0

(x+3)^2 +(y−5)^2 =45 A(0;11) of the circle to the point of trying to find the angular coefficient.

$$\left(\boldsymbol{\mathrm{x}}+\mathrm{3}\right)^{\mathrm{2}} +\left(\boldsymbol{\mathrm{y}}−\mathrm{5}\right)^{\mathrm{2}} =\mathrm{45}\:\:\:\boldsymbol{\mathrm{A}}\left(\mathrm{0};\mathrm{11}\right) \\ $$$$\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{circle}}\:\:\boldsymbol{\mathrm{to}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{point}}\:\:\boldsymbol{\mathrm{of}} \\ $$$$\boldsymbol{\mathrm{trying}}\:\:\boldsymbol{\mathrm{to}}\:\:\boldsymbol{\mathrm{find}}\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{angular}}\:\:\boldsymbol{\mathrm{coefficient}}. \\ $$

Question Number 12814 Answers: 1 Comments: 2

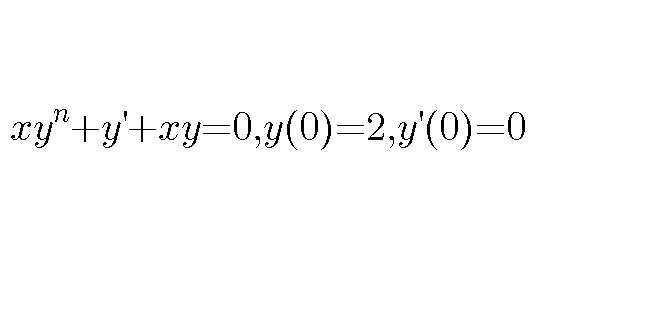
Question Number 12708 Answers: 0 Comments: 0

what′s values 𝛂. y=2e^x −𝛂e^(−x) +(2𝛂+1)x−3 will feature all of the outlets growing.

$$\boldsymbol{\mathrm{what}}'\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{values}}\:\:\boldsymbol{\alpha}. \\ $$$$\boldsymbol{\mathrm{y}}=\mathrm{2}\boldsymbol{\mathrm{e}}^{\boldsymbol{\mathrm{x}}} −\boldsymbol{\alpha\mathrm{e}}^{−\boldsymbol{\mathrm{x}}} +\left(\mathrm{2}\boldsymbol{\alpha}+\mathrm{1}\right)\boldsymbol{\mathrm{x}}−\mathrm{3} \\ $$$$\boldsymbol{\mathrm{will}}\:\:\boldsymbol{\mathrm{feature}}\:\:\boldsymbol{\mathrm{all}}\:\:\boldsymbol{\mathrm{of}}\:\:\boldsymbol{\mathrm{the}}\:\:\boldsymbol{\mathrm{outlets}} \\ $$$$\boldsymbol{\mathrm{growing}}. \\ $$

Pg 58 Pg 59 Pg 60 Pg 61 Pg 62 Pg 63 Pg 64 Pg 65 Pg 66 Pg 67

Terms of Service

Contact: info@tinkutara.com