
Question Number 68331 by Peculiar last updated on 08/Sep/19
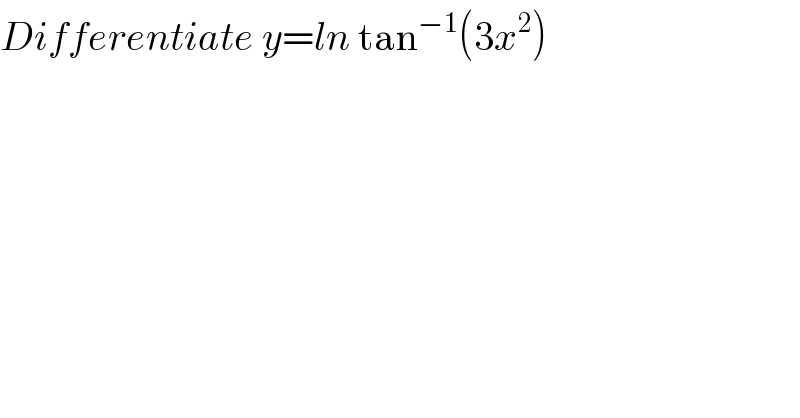
$${Differentiate}\:{y}={ln}\:\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}{x}^{\mathrm{2}} \underset{} {\right)} \\ $$
Answered by MJS last updated on 08/Sep/19
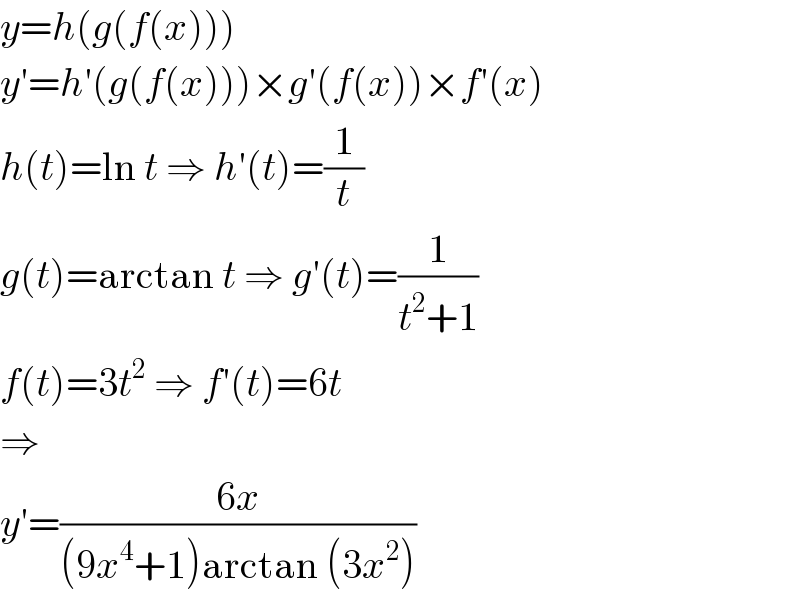
$${y}={h}\left({g}\left({f}\left({x}\right)\right)\right) \\ $$$${y}'={h}'\left({g}\left({f}\left({x}\right)\right)\right)×{g}'\left({f}\left({x}\right)\right)×{f}'\left({x}\right) \\ $$$${h}\left({t}\right)=\mathrm{ln}\:{t}\:\Rightarrow\:{h}'\left({t}\right)=\frac{\mathrm{1}}{{t}} \\ $$$${g}\left({t}\right)=\mathrm{arctan}\:{t}\:\Rightarrow\:{g}'\left({t}\right)=\frac{\mathrm{1}}{{t}^{\mathrm{2}} +\mathrm{1}} \\ $$$${f}\left({t}\right)=\mathrm{3}{t}^{\mathrm{2}} \:\Rightarrow\:{f}'\left({t}\right)=\mathrm{6}{t} \\ $$$$\Rightarrow \\ $$$${y}'=\frac{\mathrm{6}{x}}{\left(\mathrm{9}{x}^{\mathrm{4}} +\mathrm{1}\right)\mathrm{arctan}\:\left(\mathrm{3}{x}^{\mathrm{2}} \right)} \\ $$
Answered by peter frank last updated on 09/Sep/19
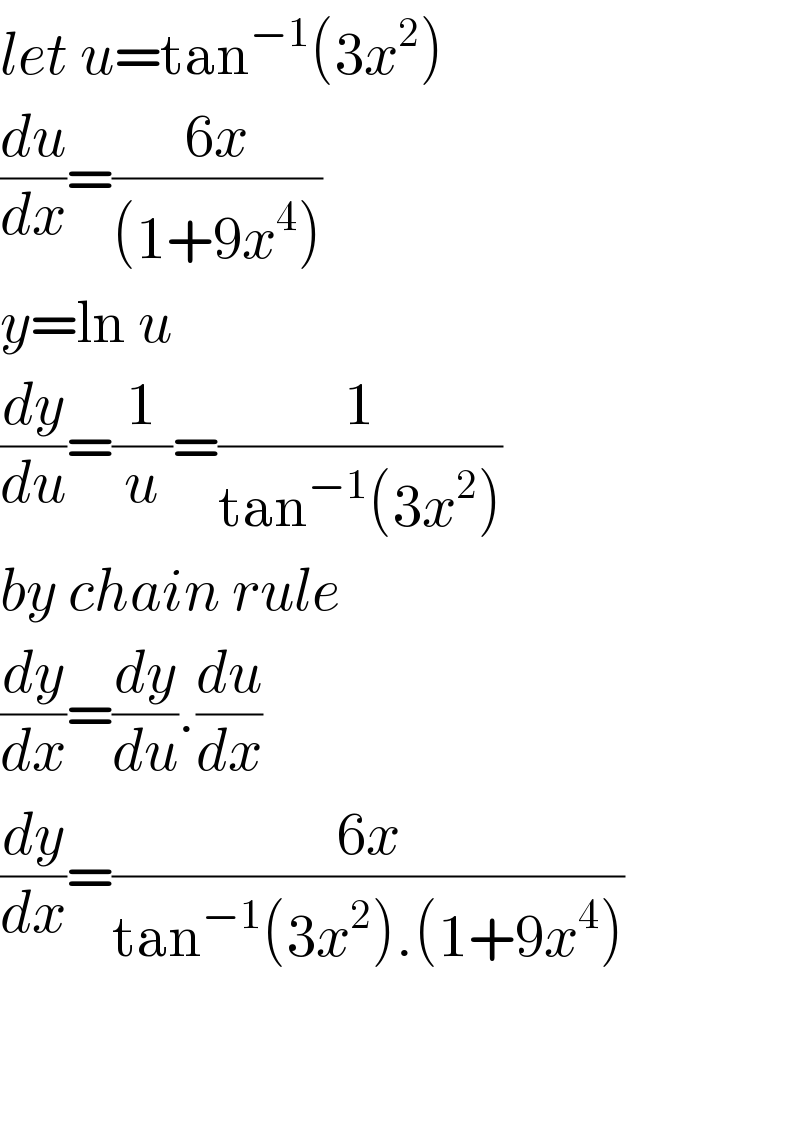
$${let}\:{u}=\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}{x}^{\mathrm{2}} \right) \\ $$$$\frac{{du}}{{dx}}=\frac{\mathrm{6}{x}}{\left(\mathrm{1}+\mathrm{9}{x}^{\mathrm{4}} \right)} \\ $$$${y}=\mathrm{ln}\:{u} \\ $$$$\frac{{dy}}{{du}}=\frac{\mathrm{1}}{{u}}=\frac{\mathrm{1}}{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}{x}^{\mathrm{2}} \right)} \\ $$$${by}\:{chain}\:{rule} \\ $$$$\frac{{dy}}{{dx}}=\frac{{dy}}{{du}}.\frac{{du}}{{dx}} \\ $$$$\frac{{dy}}{{dx}}=\frac{\mathrm{6}{x}}{\mathrm{tan}^{−\mathrm{1}} \left(\mathrm{3}{x}^{\mathrm{2}} \right).\left(\mathrm{1}+\mathrm{9}{x}^{\mathrm{4}} \right)} \\ $$$$ \\ $$$$ \\ $$
