
Question Number 192286 by pete last updated on 14/May/23
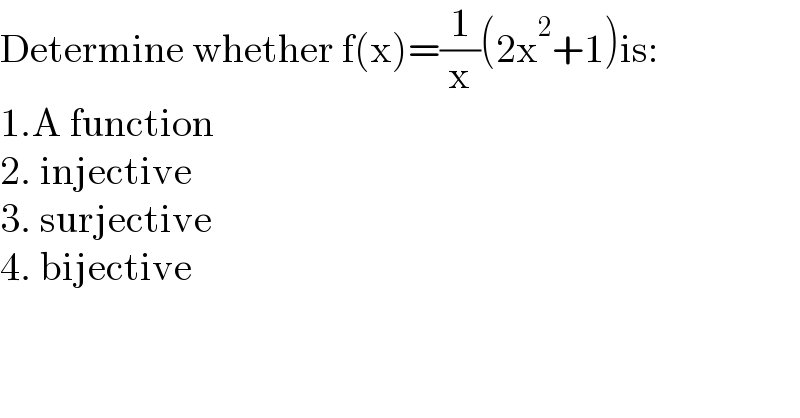
$$\mathrm{Determine}\:\mathrm{whether}\:\mathrm{f}\left(\mathrm{x}\right)=\frac{\mathrm{1}}{\mathrm{x}}\left(\mathrm{2x}^{\mathrm{2}} +\mathrm{1}\right)\mathrm{is}: \\ $$$$\mathrm{1}.\mathrm{A}\:\mathrm{function} \\ $$$$\mathrm{2}.\:\mathrm{injective} \\ $$$$\mathrm{3}.\:\mathrm{surjective} \\ $$$$\mathrm{4}.\:\mathrm{bijective} \\ $$
Answered by mehdee42 last updated on 14/May/23
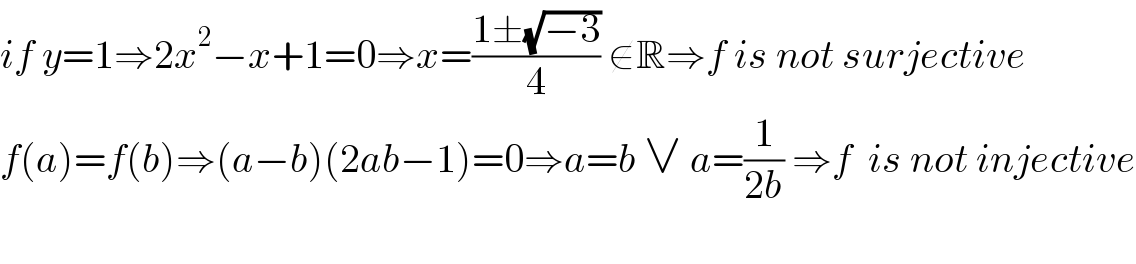
$${if}\:{y}=\mathrm{1}\Rightarrow\mathrm{2}{x}^{\mathrm{2}} −{x}+\mathrm{1}=\mathrm{0}\Rightarrow{x}=\frac{\mathrm{1}\pm\sqrt{−\mathrm{3}}}{\mathrm{4}}\:\notin\mathbb{R}\Rightarrow{f}\:{is}\:{not}\:{surjective} \\ $$$${f}\left({a}\right)={f}\left({b}\right)\Rightarrow\left({a}−{b}\right)\left(\mathrm{2}{ab}−\mathrm{1}\right)=\mathrm{0}\Rightarrow{a}={b}\:\vee\:{a}=\frac{\mathrm{1}}{\mathrm{2}{b}}\:\Rightarrow{f}\:\:{is}\:{not}\:{injective} \\ $$$$ \\ $$
Commented by mehdee42 last updated on 14/May/23
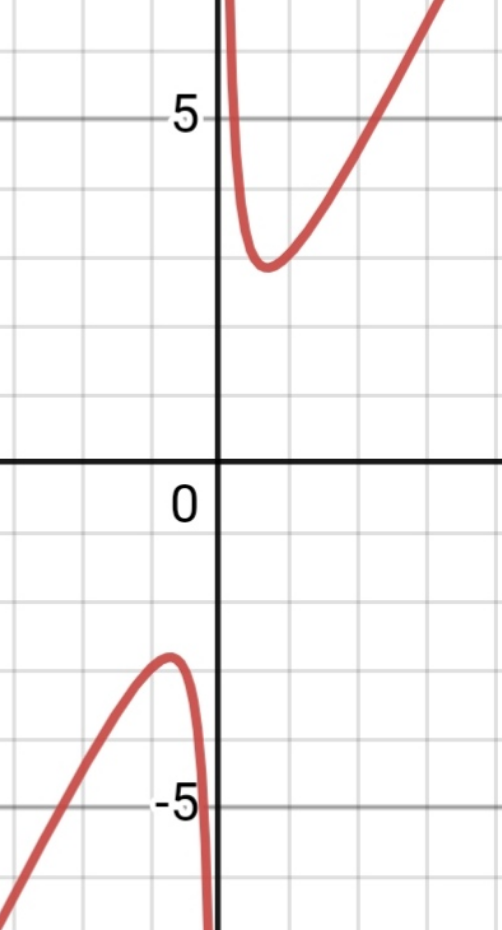
Commented by pete last updated on 14/May/23

$$\mathrm{thank}\:\mathrm{you}\:\mathrm{sir} \\ $$
