Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 84543 by niroj last updated on 14/Mar/20

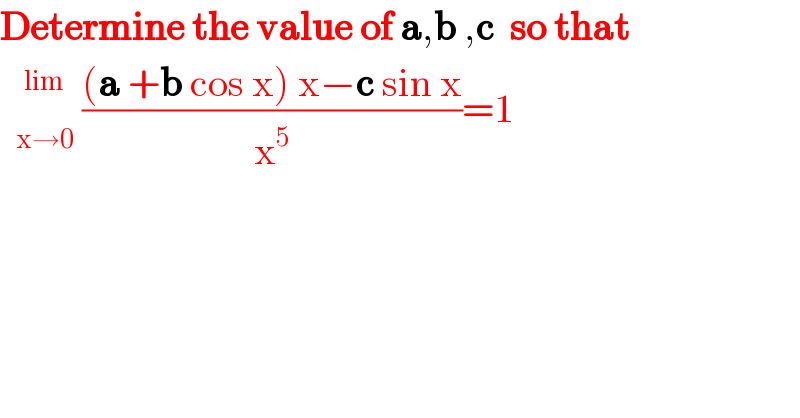
Determine the value of a,b ,c so that _(x→0) ^(lim) (((a +b cos x) x−c sin x)/x^5 )=1

$$\boldsymbol{\mathrm{Determine}}\:\boldsymbol{\mathrm{the}}\:\boldsymbol{\mathrm{value}}\:\boldsymbol{\mathrm{of}}\:\boldsymbol{\mathrm{a}},\boldsymbol{\mathrm{b}}\:,\boldsymbol{\mathrm{c}}\:\:\boldsymbol{\mathrm{so}}\:\boldsymbol{\mathrm{that}} \\ $$$$\:\:\underset{\mathrm{x}\rightarrow\mathrm{0}} {\overset{\mathrm{lim}} {\:}}\:\frac{\left(\boldsymbol{\mathrm{a}}\:+\boldsymbol{\mathrm{b}}\:\mathrm{cos}\:\mathrm{x}\right)\:\mathrm{x}−\boldsymbol{\mathrm{c}}\:\mathrm{sin}\:\mathrm{x}}{\mathrm{x}^{\mathrm{5}} }=\mathrm{1} \\ $$

Commented by mr W last updated on 14/Mar/20

a=120 b=60 c=180

$${a}=\mathrm{120} \\ $$$${b}=\mathrm{60} \\ $$$${c}=\mathrm{180} \\ $$

Commented by jagoll last updated on 14/Mar/20

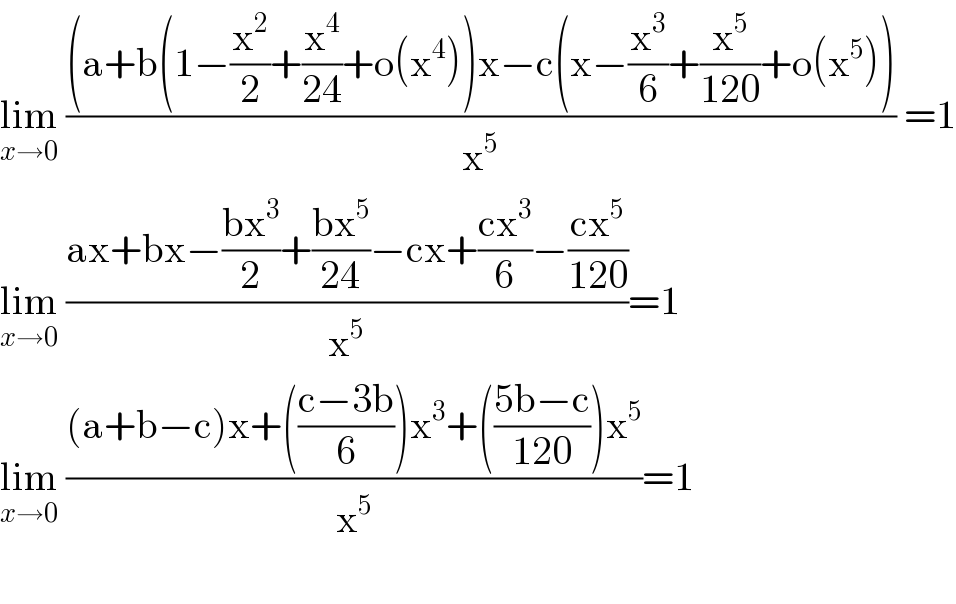
lim_(x→0) (((a+b(1−(x^2 /2)+(x^4 /(24))+o(x^4 ))x−c(x−(x^3 /6)+(x^5 /(120))+o(x^5 )))/x^5 ) =1 lim_(x→0) ((ax+bx−((bx^3 )/2)+((bx^5 )/(24))−cx+((cx^3 )/6)−((cx^5 )/(120)))/x^5 )=1 lim_(x→0) (((a+b−c)x+(((c−3b)/6))x^3 +(((5b−c)/(120)))x^5 )/x^5 )=1

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{a}+\mathrm{b}\left(\mathrm{1}−\frac{\mathrm{x}^{\mathrm{2}} }{\mathrm{2}}+\frac{\mathrm{x}^{\mathrm{4}} }{\mathrm{24}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{4}} \right)\right)\mathrm{x}−\mathrm{c}\left(\mathrm{x}−\frac{\mathrm{x}^{\mathrm{3}} }{\mathrm{6}}+\frac{\mathrm{x}^{\mathrm{5}} }{\mathrm{120}}+\mathrm{o}\left(\mathrm{x}^{\mathrm{5}} \right)\right)\right.}{\mathrm{x}^{\mathrm{5}} }\:=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\mathrm{ax}+\mathrm{bx}−\frac{\mathrm{bx}^{\mathrm{3}} }{\mathrm{2}}+\frac{\mathrm{bx}^{\mathrm{5}} }{\mathrm{24}}−\mathrm{cx}+\frac{\mathrm{cx}^{\mathrm{3}} }{\mathrm{6}}−\frac{\mathrm{cx}^{\mathrm{5}} }{\mathrm{120}}}{\mathrm{x}^{\mathrm{5}} }=\mathrm{1} \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{\left(\mathrm{a}+\mathrm{b}−\mathrm{c}\right)\mathrm{x}+\left(\frac{\mathrm{c}−\mathrm{3b}}{\mathrm{6}}\right)\mathrm{x}^{\mathrm{3}} +\left(\frac{\mathrm{5b}−\mathrm{c}}{\mathrm{120}}\right)\mathrm{x}^{\mathrm{5}} }{\mathrm{x}^{\mathrm{5}} }=\mathrm{1} \\ $$$$ \\ $$

Commented by jagoll last updated on 14/Mar/20

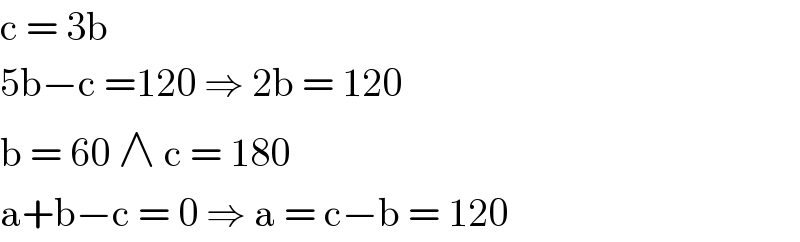
c = 3b 5b−c =120 ⇒ 2b = 120 b = 60 ∧ c = 180 a+b−c = 0 ⇒ a = c−b = 120

$$\mathrm{c}\:=\:\mathrm{3b} \\ $$$$\mathrm{5b}−\mathrm{c}\:=\mathrm{120}\:\Rightarrow\:\mathrm{2b}\:=\:\mathrm{120}\: \\ $$$$\mathrm{b}\:=\:\mathrm{60}\:\wedge\:\mathrm{c}\:=\:\mathrm{180} \\ $$$$\mathrm{a}+\mathrm{b}−\mathrm{c}\:=\:\mathrm{0}\:\Rightarrow\:\mathrm{a}\:=\:\mathrm{c}−\mathrm{b}\:=\:\mathrm{120} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com