
Question Number 18884 by Tinkutara last updated on 31/Jul/17

$$\mathrm{Determine}\:\mathrm{the}\:\mathrm{smallest}\:\mathrm{positive}\:\mathrm{integer} \\ $$$$\mathrm{x},\:\mathrm{whose}\:\mathrm{last}\:\mathrm{digit}\:\mathrm{is}\:\mathrm{6}\:\mathrm{and}\:\mathrm{if}\:\mathrm{we}\:\mathrm{erase} \\ $$$$\mathrm{this}\:\mathrm{6}\:\mathrm{and}\:\mathrm{put}\:\mathrm{it}\:\mathrm{in}\:\mathrm{left}\:\mathrm{most}\:\mathrm{of}\:\mathrm{the} \\ $$$$\mathrm{number}\:\mathrm{so}\:\mathrm{obtained},\:\mathrm{the}\:\mathrm{number} \\ $$$$\mathrm{becomes}\:\mathrm{4x}. \\ $$
Answered by mrW1 last updated on 01/Aug/17
![let′s say the number has n+1 digits let x=[abcd...pqr6]=10u+6 let y=[6abcd...pqr]=6×10^n +u y=4x ⇒6×10^n +u=4(10u+6) ⇒6(10^n −4)=39u ⇒2(2^n ×5^n −2^2 )=13u ⇒2^3 (2^(n−2) ×5^n −1)=13u ⇒2^3 (25×10^(n−2) −1)=13u ⇒u=((2^3 (25×10^(n−2) −1))/(13)) ⇒25×10^(n−2) −1=13k the smallest n=5: 25×10^(5−2) −1=25000−1=24999=13×1923 ⇒min. u=2^3 ×1923=15384 ⇒min. x=153846 the further numbers are: x=153846153846 x=153846153846153846 x=153846153846153846153846 ......](Q18887.png)
$$\mathrm{let}'\mathrm{s}\:\mathrm{say}\:\mathrm{the}\:\mathrm{number}\:\mathrm{has}\:\mathrm{n}+\mathrm{1}\:\mathrm{digits} \\ $$$$\mathrm{let}\:\mathrm{x}=\left[\mathrm{abcd}...\mathrm{pqr6}\right]=\mathrm{10u}+\mathrm{6} \\ $$$$\mathrm{let}\:\mathrm{y}=\left[\mathrm{6abcd}...\mathrm{pqr}\right]=\mathrm{6}×\mathrm{10}^{\mathrm{n}} +\mathrm{u} \\ $$$$\mathrm{y}=\mathrm{4x} \\ $$$$\Rightarrow\mathrm{6}×\mathrm{10}^{\mathrm{n}} +\mathrm{u}=\mathrm{4}\left(\mathrm{10u}+\mathrm{6}\right) \\ $$$$\Rightarrow\mathrm{6}\left(\mathrm{10}^{\mathrm{n}} −\mathrm{4}\right)=\mathrm{39u} \\ $$$$\Rightarrow\mathrm{2}\left(\mathrm{2}^{\mathrm{n}} ×\mathrm{5}^{\mathrm{n}} −\mathrm{2}^{\mathrm{2}} \right)=\mathrm{13u} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{3}} \left(\mathrm{2}^{\mathrm{n}−\mathrm{2}} ×\mathrm{5}^{\mathrm{n}} −\mathrm{1}\right)=\mathrm{13u} \\ $$$$\Rightarrow\mathrm{2}^{\mathrm{3}} \left(\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}\right)=\mathrm{13u} \\ $$$$\Rightarrow\mathrm{u}=\frac{\mathrm{2}^{\mathrm{3}} \left(\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}\right)}{\mathrm{13}} \\ $$$$\Rightarrow\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}=\mathrm{13k} \\ $$$$\mathrm{the}\:\mathrm{smallest}\:\mathrm{n}=\mathrm{5}: \\ $$$$\mathrm{25}×\mathrm{10}^{\mathrm{5}−\mathrm{2}} −\mathrm{1}=\mathrm{25000}−\mathrm{1}=\mathrm{24999}=\mathrm{13}×\mathrm{1923} \\ $$$$\Rightarrow\mathrm{min}.\:\mathrm{u}=\mathrm{2}^{\mathrm{3}} ×\mathrm{1923}=\mathrm{15384} \\ $$$$\Rightarrow\mathrm{min}.\:\mathrm{x}=\mathrm{153846} \\ $$$$ \\ $$$$\mathrm{the}\:\mathrm{further}\:\mathrm{numbers}\:\mathrm{are}: \\ $$$$\mathrm{x}=\mathrm{153846153846} \\ $$$$\mathrm{x}=\mathrm{153846153846153846} \\ $$$$\mathrm{x}=\mathrm{153846153846153846153846} \\ $$$$...... \\ $$
Commented by Tinkutara last updated on 01/Aug/17
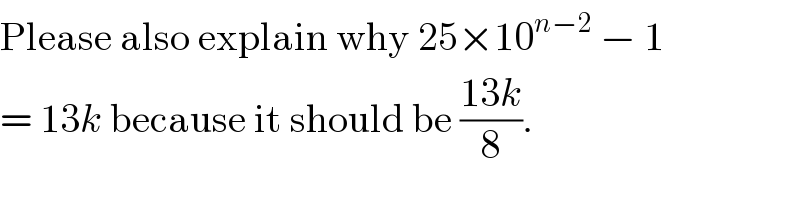
$$\mathrm{Please}\:\mathrm{also}\:\mathrm{explain}\:\mathrm{why}\:\mathrm{25}×\mathrm{10}^{{n}−\mathrm{2}} \:−\:\mathrm{1} \\ $$$$=\:\mathrm{13}{k}\:\mathrm{because}\:\mathrm{it}\:\mathrm{should}\:\mathrm{be}\:\frac{\mathrm{13}{k}}{\mathrm{8}}. \\ $$
Commented by mrW1 last updated on 01/Aug/17
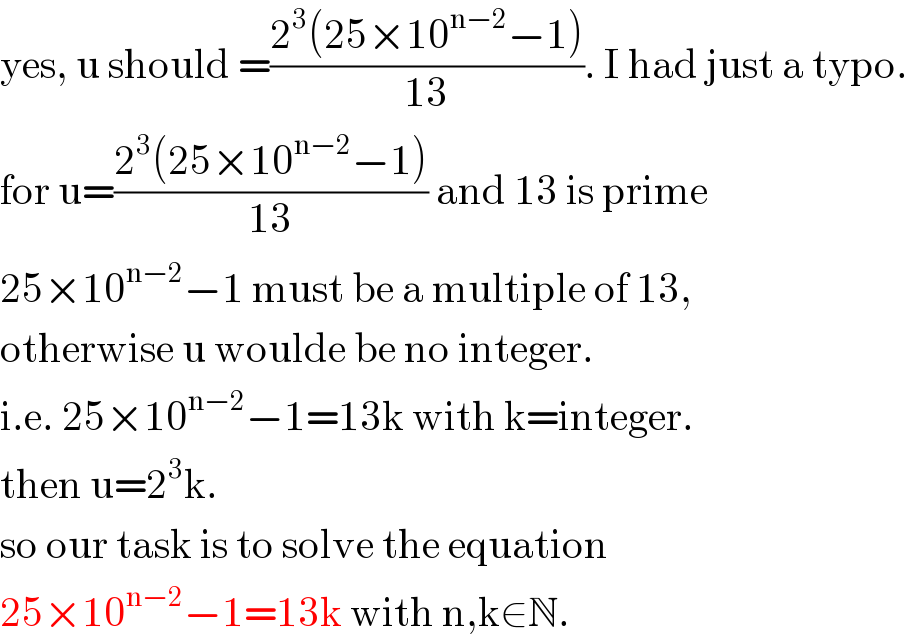
$$\mathrm{yes},\:\mathrm{u}\:\mathrm{should}\:=\frac{\mathrm{2}^{\mathrm{3}} \left(\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}\right)}{\mathrm{13}}.\:\mathrm{I}\:\mathrm{had}\:\mathrm{just}\:\mathrm{a}\:\mathrm{typo}. \\ $$$$\mathrm{for}\:\mathrm{u}=\frac{\mathrm{2}^{\mathrm{3}} \left(\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}\right)}{\mathrm{13}}\:\mathrm{and}\:\mathrm{13}\:\mathrm{is}\:\mathrm{prime} \\ $$$$\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}\:\mathrm{must}\:\mathrm{be}\:\mathrm{a}\:\mathrm{multiple}\:\mathrm{of}\:\mathrm{13}, \\ $$$$\mathrm{otherwise}\:\mathrm{u}\:\mathrm{woulde}\:\mathrm{be}\:\mathrm{no}\:\mathrm{integer}. \\ $$$$\mathrm{i}.\mathrm{e}.\:\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}=\mathrm{13k}\:\mathrm{with}\:\mathrm{k}=\mathrm{integer}. \\ $$$$\mathrm{then}\:\mathrm{u}=\mathrm{2}^{\mathrm{3}} \mathrm{k}. \\ $$$$\mathrm{so}\:\mathrm{our}\:\mathrm{task}\:\mathrm{is}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the}\:\mathrm{equation} \\ $$$$\mathrm{25}×\mathrm{10}^{\mathrm{n}−\mathrm{2}} −\mathrm{1}=\mathrm{13k}\:\mathrm{with}\:\mathrm{n},\mathrm{k}\in\mathbb{N}. \\ $$
Commented by mrW1 last updated on 01/Aug/17

$$\mathrm{certainly}\:\mathrm{you}\:\mathrm{can}\:\mathrm{solve}\:\mathrm{this}\:\mathrm{question} \\ $$$$\mathrm{directly}\:\mathrm{like}\:\mathrm{this}: \\ $$$$\:\:\:\:\:\:\:\:\:\mathrm{abcdef6} \\ $$$$\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:\:×\mathrm{4} \\ $$$$−−−−−−−−− \\ $$$$\:=\:\:\:\:\mathrm{6abcdef} \\ $$$$\Rightarrow\mathrm{f}=\mathrm{4} \\ $$$$\Rightarrow\mathrm{e}=\mathrm{8} \\ $$$$\Rightarrow\mathrm{d}=\mathrm{3} \\ $$$$\Rightarrow\mathrm{c}=\mathrm{5} \\ $$$$\Rightarrow\mathrm{b}=\mathrm{1} \\ $$$$\Rightarrow\mathrm{a}=\mathrm{6}\:!\:\mathrm{that}'\mathrm{s}\:\mathrm{right}.\:\Rightarrow\:\mathrm{our}\:\mathrm{first}\:\mathrm{number}\:\mathrm{is}\:\mathrm{153846} \\ $$$$\mathrm{just}\:\mathrm{go}\:\mathrm{on}\:\mathrm{with}\:\mathrm{these}\:\mathrm{steps}\:\mathrm{if}\:\mathrm{you}\:\mathrm{want}\:\mathrm{to}\:\mathrm{get}\:\mathrm{the} \\ $$$$\mathrm{next}\:\mathrm{suitable}\:\mathrm{number}. \\ $$
Commented by Tinkutara last updated on 01/Aug/17

$$\mathrm{Thank}\:\mathrm{you}\:\mathrm{very}\:\mathrm{much}\:\mathrm{mrW1}\:\mathrm{Sir}! \\ $$
Commented by mrW1 last updated on 01/Aug/17

$$\mathrm{I}\:\mathrm{tried}\:\mathrm{to}\:\mathrm{use}\:\mathrm{an}\:\mathrm{equation}\:\mathrm{to}\:\mathrm{solve}\:\mathrm{the} \\ $$$$\mathrm{question},\:\mathrm{because}\:\mathrm{the}\:\mathrm{question}\:\mathrm{can} \\ $$$$\mathrm{be}\:\mathrm{generalised}: \\ $$$$\mathrm{Find}\:\mathrm{such}\:\mathrm{numbers}\:\mathrm{when}\:\mathrm{we}\:\mathrm{erase}\:\mathrm{their}\:\mathrm{last} \\ $$$$\mathrm{digit}\:\mathrm{and}\:\mathrm{put}\:\mathrm{it}\:\mathrm{before}\:\mathrm{the}\:\mathrm{first}\:\mathrm{digit}, \\ $$$$\mathrm{the}\:\mathrm{new}\:\mathrm{number}\:\mathrm{will}\:\mathrm{be}\:\mathrm{m}\:\mathrm{times}\:\mathrm{as} \\ $$$$\mathrm{the}\:\mathrm{original}\:\mathrm{number}. \\ $$$$\mathrm{m}\:\mathrm{can}\:\mathrm{be}\:\mathrm{2}\:\mathrm{til}\:\mathrm{9}. \\ $$
Commented by Tinkutara last updated on 01/Aug/17
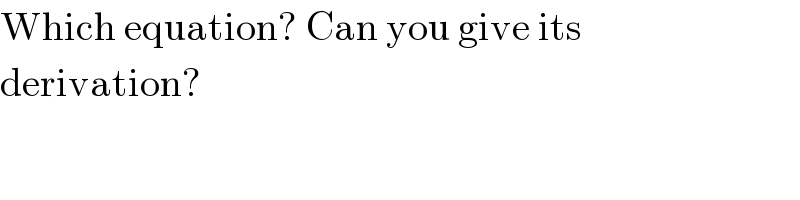
$$\mathrm{Which}\:\mathrm{equation}?\:\mathrm{Can}\:\mathrm{you}\:\mathrm{give}\:\mathrm{its} \\ $$$$\mathrm{derivation}? \\ $$
