
Question Number 1766 by Rasheed Ahmad last updated on 18/Sep/15
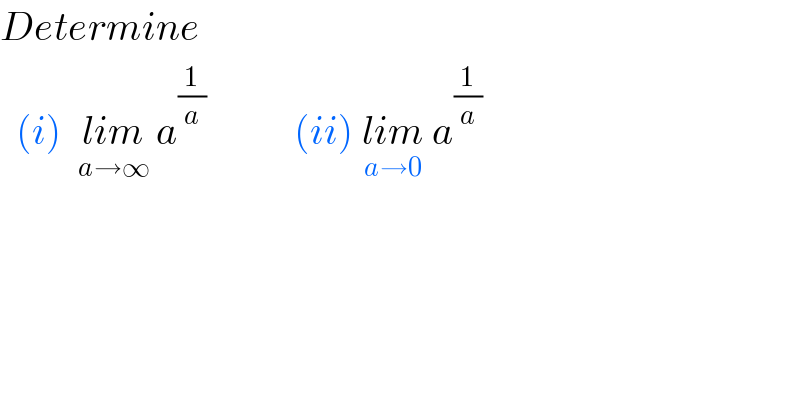
$${Determine}\: \\ $$$$\:\:\left({i}\right)\:\:\underset{{a}\rightarrow\infty} {{lim}}\:{a}^{\frac{\mathrm{1}}{{a}}} \:\:\:\:\:\:\:\:\:\:\:\left({ii}\right)\:\underset{{a}\rightarrow\mathrm{0}} {{lim}}\:{a}^{\frac{\mathrm{1}}{{a}}} \\ $$
Answered by 123456 last updated on 19/Sep/15
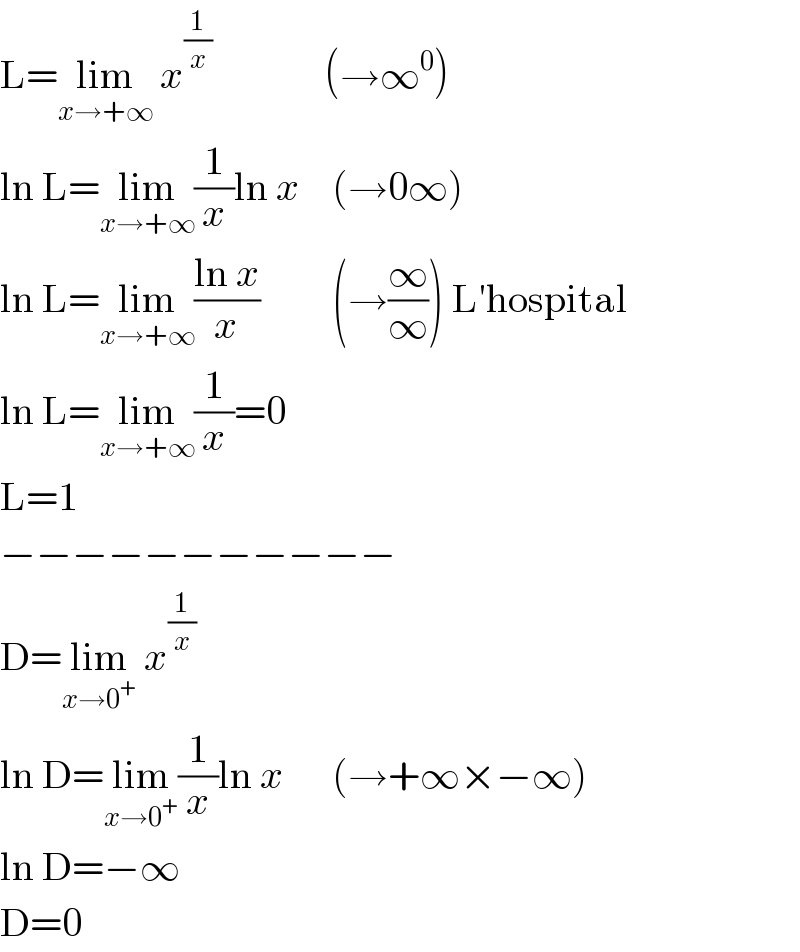
$$\mathrm{L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\:{x}^{\frac{\mathrm{1}}{{x}}} \:\:\:\:\:\:\:\:\:\:\:\:\:\:\left(\rightarrow\infty^{\mathrm{0}} \right) \\ $$$$\mathrm{ln}\:\mathrm{L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\mathrm{ln}\:{x}\:\:\:\:\left(\rightarrow\mathrm{0}\infty\right) \\ $$$$\mathrm{ln}\:\mathrm{L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{ln}\:{x}}{{x}}\:\:\:\:\:\:\:\:\:\left(\rightarrow\frac{\infty}{\infty}\right)\:\mathrm{L}'\mathrm{hospital} \\ $$$$\mathrm{ln}\:\mathrm{L}=\underset{{x}\rightarrow+\infty} {\mathrm{lim}}\frac{\mathrm{1}}{{x}}=\mathrm{0} \\ $$$$\mathrm{L}=\mathrm{1} \\ $$$$−−−−−−−−−−− \\ $$$$\mathrm{D}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\:{x}^{\frac{\mathrm{1}}{{x}}} \\ $$$$\mathrm{ln}\:\mathrm{D}=\underset{{x}\rightarrow\mathrm{0}^{+} } {\mathrm{lim}}\frac{\mathrm{1}}{{x}}\mathrm{ln}\:{x}\:\:\:\:\:\:\left(\rightarrow+\infty×−\infty\right) \\ $$$$\mathrm{ln}\:\mathrm{D}=−\infty \\ $$$$\mathrm{D}=\mathrm{0} \\ $$
