Question and Answers Forum

All Questions      Topic List

Relation and Functions Questions

Previous in All Question      Next in All Question      

Previous in Relation and Functions      Next in Relation and Functions      

Question Number 97648 by bobhans last updated on 09/Jun/20

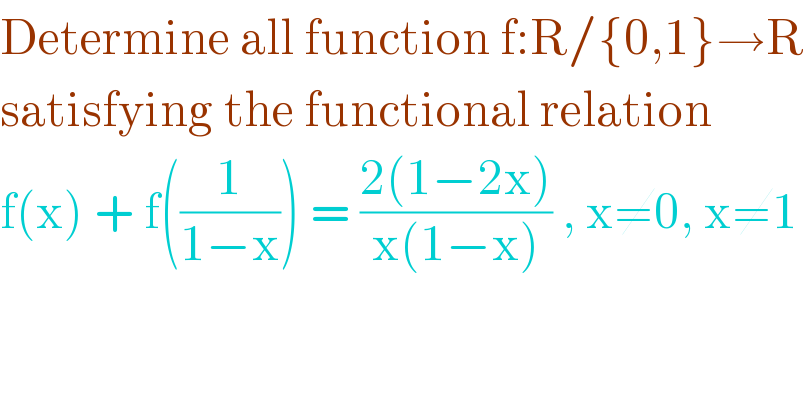
Determine all function f:R/{0,1}→R satisfying the functional relation f(x) + f((1/(1−x))) = ((2(1−2x))/(x(1−x))) , x≠0, x≠1

$$\mathrm{Determine}\:\mathrm{all}\:\mathrm{function}\:\mathrm{f}:\mathrm{R}/\left\{\mathrm{0},\mathrm{1}\right\}\rightarrow\mathrm{R} \\ $$$$\mathrm{satisfying}\:\mathrm{the}\:\mathrm{functional}\:\mathrm{relation} \\ $$$$\mathrm{f}\left(\mathrm{x}\right)\:+\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\frac{\mathrm{2}\left(\mathrm{1}−\mathrm{2x}\right)}{\mathrm{x}\left(\mathrm{1}−\mathrm{x}\right)}\:,\:\mathrm{x}\neq\mathrm{0},\:\mathrm{x}\neq\mathrm{1} \\ $$

Commented by bemath last updated on 09/Jun/20

nice question

$$\mathrm{nice}\:\mathrm{question} \\ $$

Answered by bemath last updated on 09/Jun/20

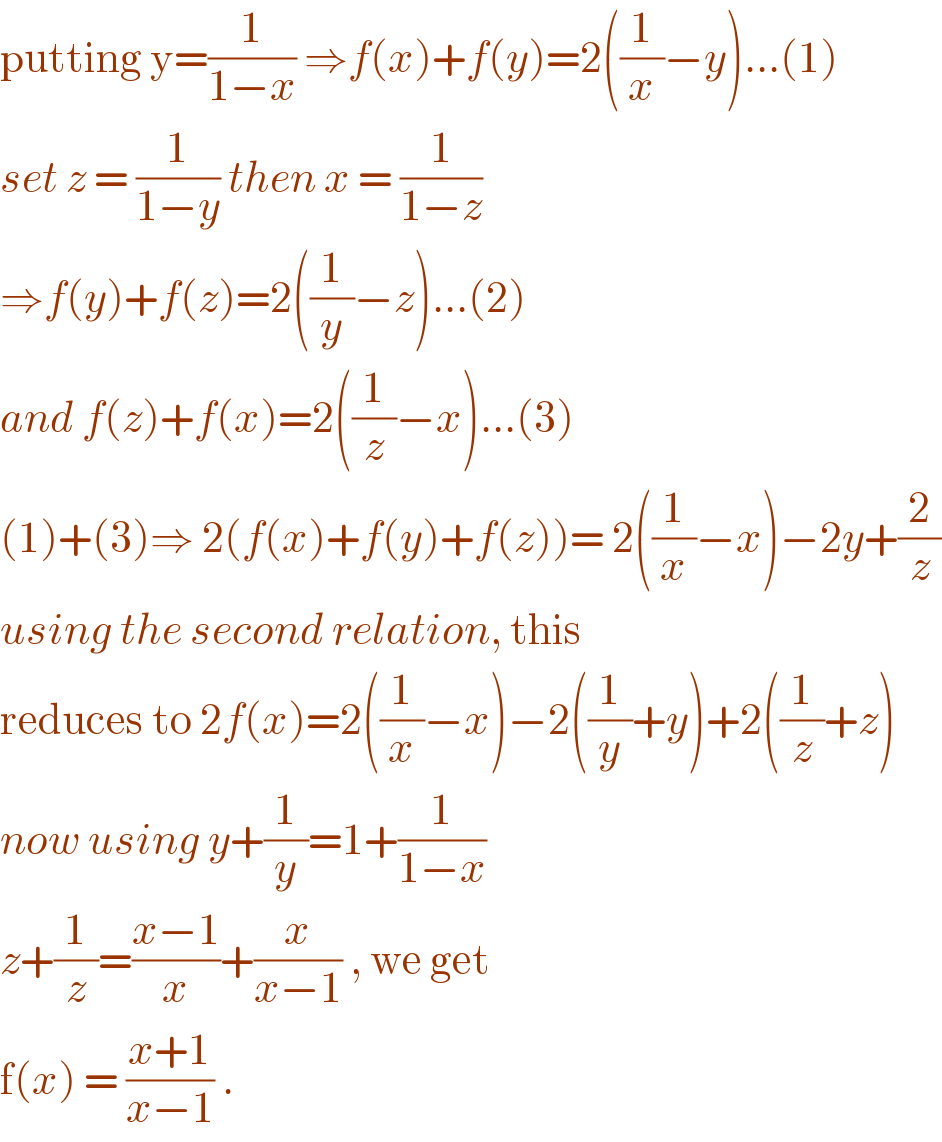
putting y=(1/(1−x)) ⇒f(x)+f(y)=2((1/x)−y)...(1) set z = (1/(1−y)) then x = (1/(1−z)) ⇒f(y)+f(z)=2((1/y)−z)...(2) and f(z)+f(x)=2((1/z)−x)...(3) (1)+(3)⇒ 2(f(x)+f(y)+f(z))= 2((1/x)−x)−2y+(2/z) using the second relation, this reduces to 2f(x)=2((1/x)−x)−2((1/y)+y)+2((1/z)+z) now using y+(1/y)=1+(1/(1−x)) z+(1/z)=((x−1)/x)+(x/(x−1)) , we get f(x) = ((x+1)/(x−1)) .

$$\mathrm{putting}\:\mathrm{y}=\frac{\mathrm{1}}{\mathrm{1}−{x}}\:\Rightarrow{f}\left({x}\right)+{f}\left({y}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{x}}−{y}\right)...\left(\mathrm{1}\right) \\ $$$${set}\:{z}\:=\:\frac{\mathrm{1}}{\mathrm{1}−{y}}\:{then}\:{x}\:=\:\frac{\mathrm{1}}{\mathrm{1}−{z}} \\ $$$$\Rightarrow{f}\left({y}\right)+{f}\left({z}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{y}}−{z}\right)...\left(\mathrm{2}\right) \\ $$$${and}\:{f}\left({z}\right)+{f}\left({x}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{z}}−{x}\right)...\left(\mathrm{3}\right) \\ $$$$\left(\mathrm{1}\right)+\left(\mathrm{3}\right)\Rightarrow\:\mathrm{2}\left({f}\left({x}\right)+{f}\left({y}\right)+{f}\left({z}\right)\right)=\:\mathrm{2}\left(\frac{\mathrm{1}}{{x}}−{x}\right)−\mathrm{2}{y}+\frac{\mathrm{2}}{{z}} \\ $$$${using}\:{the}\:{second}\:{relation},\:\mathrm{this} \\ $$$$\mathrm{reduces}\:\mathrm{to}\:\mathrm{2}{f}\left({x}\right)=\mathrm{2}\left(\frac{\mathrm{1}}{{x}}−{x}\right)−\mathrm{2}\left(\frac{\mathrm{1}}{{y}}+{y}\right)+\mathrm{2}\left(\frac{\mathrm{1}}{{z}}+{z}\right) \\ $$$${now}\:{using}\:{y}+\frac{\mathrm{1}}{{y}}=\mathrm{1}+\frac{\mathrm{1}}{\mathrm{1}−{x}} \\ $$$${z}+\frac{\mathrm{1}}{{z}}=\frac{{x}−\mathrm{1}}{{x}}+\frac{{x}}{{x}−\mathrm{1}}\:,\:\mathrm{we}\:\mathrm{get} \\ $$$$\mathrm{f}\left({x}\right)\:=\:\frac{{x}+\mathrm{1}}{{x}−\mathrm{1}}\:. \\ $$

Commented by bobhans last updated on 09/Jun/20

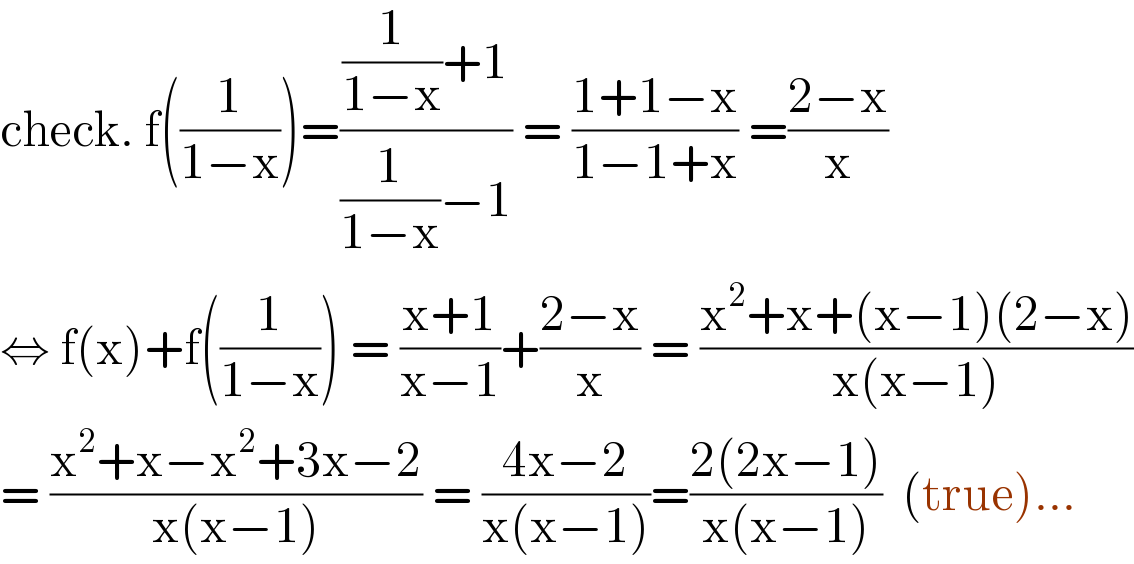
check. f((1/(1−x)))=(((1/(1−x))+1)/((1/(1−x))−1)) = ((1+1−x)/(1−1+x)) =((2−x)/x) ⇔ f(x)+f((1/(1−x))) = ((x+1)/(x−1))+((2−x)/x) = ((x^2 +x+(x−1)(2−x))/(x(x−1))) = ((x^2 +x−x^2 +3x−2)/(x(x−1))) = ((4x−2)/(x(x−1)))=((2(2x−1))/(x(x−1))) (true)...

$$\mathrm{check}.\:\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)=\frac{\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}+\mathrm{1}}{\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}−\mathrm{1}}\:=\:\frac{\mathrm{1}+\mathrm{1}−\mathrm{x}}{\mathrm{1}−\mathrm{1}+\mathrm{x}}\:=\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}} \\ $$$$\Leftrightarrow\:\mathrm{f}\left(\mathrm{x}\right)+\mathrm{f}\left(\frac{\mathrm{1}}{\mathrm{1}−\mathrm{x}}\right)\:=\:\frac{\mathrm{x}+\mathrm{1}}{\mathrm{x}−\mathrm{1}}+\frac{\mathrm{2}−\mathrm{x}}{\mathrm{x}}\:=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}+\left(\mathrm{x}−\mathrm{1}\right)\left(\mathrm{2}−\mathrm{x}\right)}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)} \\ $$$$=\:\frac{\mathrm{x}^{\mathrm{2}} +\mathrm{x}−\mathrm{x}^{\mathrm{2}} +\mathrm{3x}−\mathrm{2}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}\:=\:\frac{\mathrm{4x}−\mathrm{2}}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}=\frac{\mathrm{2}\left(\mathrm{2x}−\mathrm{1}\right)}{\mathrm{x}\left(\mathrm{x}−\mathrm{1}\right)}\:\:\left(\mathrm{true}\right)... \\ $$

Commented by bemath last updated on 09/Jun/20

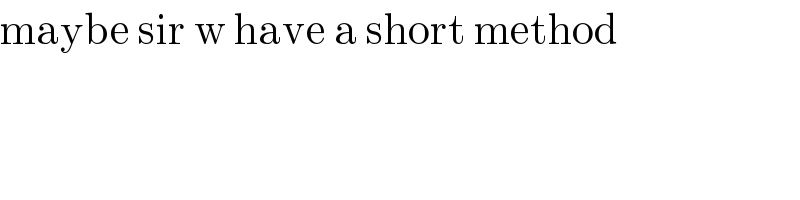
maybe sir w have a short method

$$\mathrm{maybe}\:\mathrm{sir}\:\mathrm{w}\:\mathrm{have}\:\mathrm{a}\:\mathrm{short}\:\mathrm{method} \\ $$

Commented by john santu last updated on 09/Jun/20

very.....coollll

$$\mathrm{very}.....\mathrm{coollll} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com