
Question Number 203146 by Rasheed.Sindhi last updated on 11/Jan/24
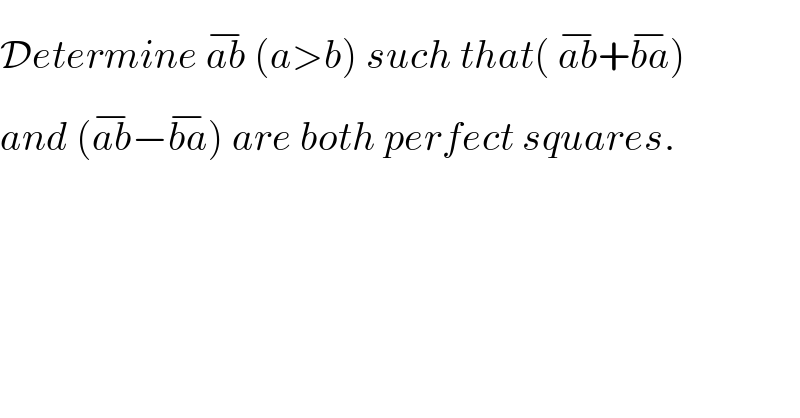
$$\mathcal{D}{etermine}\:\overline {{ab}}\:\left({a}>{b}\right)\:{such}\:{that}\left(\:\overline {{ab}}+\overline {{ba}}\right)\: \\ $$$${and}\:\left(\overline {{ab}}−\overline {{ba}}\right)\:{are}\:{both}\:{perfect}\:{squares}. \\ $$
Answered by Frix last updated on 11/Jan/24
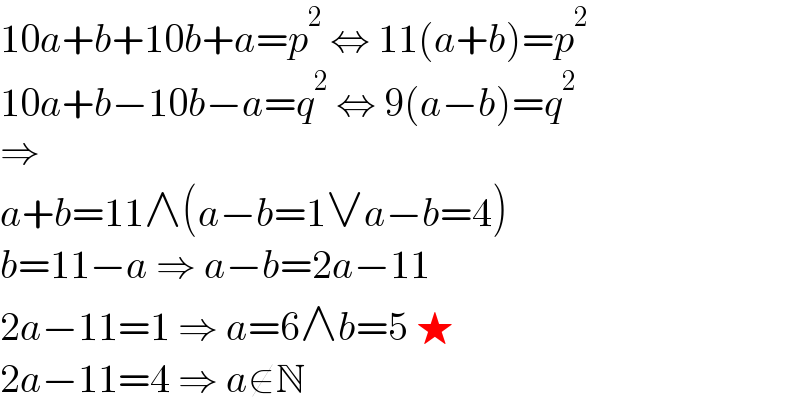
$$\mathrm{10}{a}+{b}+\mathrm{10}{b}+{a}={p}^{\mathrm{2}} \:\Leftrightarrow\:\mathrm{11}\left({a}+{b}\right)={p}^{\mathrm{2}} \\ $$$$\mathrm{10}{a}+{b}−\mathrm{10}{b}−{a}={q}^{\mathrm{2}} \:\Leftrightarrow\:\mathrm{9}\left({a}−{b}\right)={q}^{\mathrm{2}} \\ $$$$\Rightarrow \\ $$$${a}+{b}=\mathrm{11}\wedge\left({a}−{b}=\mathrm{1}\vee{a}−{b}=\mathrm{4}\right) \\ $$$${b}=\mathrm{11}−{a}\:\Rightarrow\:{a}−{b}=\mathrm{2}{a}−\mathrm{11} \\ $$$$\mathrm{2}{a}−\mathrm{11}=\mathrm{1}\:\Rightarrow\:{a}=\mathrm{6}\wedge{b}=\mathrm{5}\:\bigstar \\ $$$$\mathrm{2}{a}−\mathrm{11}=\mathrm{4}\:\Rightarrow\:{a}\notin\mathbb{N} \\ $$
Commented by Rasheed.Sindhi last updated on 11/Jan/24

$$\mathbb{T}\boldsymbol{\mathrm{han}}\Bbbk\boldsymbol{\mathrm{s}}\:\boldsymbol{\mathrm{sir}}! \\ $$
