
Question Number 215730 by MathematicalUser2357 last updated on 16/Jan/25
![Determine a, b, c [Lazy problem] J181-2. x^3 −6x^2 +15x−7=(x+a)^3 +bx+c J182-(1) x^3 +ax+2=(x+1)(x^2 +bx+c)](Q215730.png)
$$\boldsymbol{\mathrm{Determine}}\:\boldsymbol{{a}},\:\boldsymbol{{b}},\:\boldsymbol{{c}}\:\left[\mathrm{Lazy}\:\mathrm{problem}\right] \\ $$$$\mathrm{J181}-\mathrm{2}.\:{x}^{\mathrm{3}} −\mathrm{6}{x}^{\mathrm{2}} +\mathrm{15}{x}−\mathrm{7}=\left({x}+{a}\right)^{\mathrm{3}} +{bx}+{c} \\ $$$$\mathrm{J182}-\left(\mathrm{1}\right)\:{x}^{\mathrm{3}} +{ax}+\mathrm{2}=\left({x}+\mathrm{1}\right)\left({x}^{\mathrm{2}} +{bx}+{c}\right) \\ $$
Answered by A5T last updated on 16/Jan/25
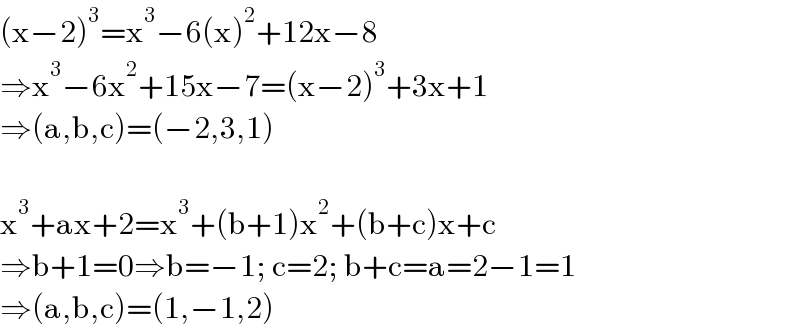
$$\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{3}} =\mathrm{x}^{\mathrm{3}} −\mathrm{6}\left(\mathrm{x}\right)^{\mathrm{2}} +\mathrm{12x}−\mathrm{8} \\ $$$$\Rightarrow\mathrm{x}^{\mathrm{3}} −\mathrm{6x}^{\mathrm{2}} +\mathrm{15x}−\mathrm{7}=\left(\mathrm{x}−\mathrm{2}\right)^{\mathrm{3}} +\mathrm{3x}+\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\left(−\mathrm{2},\mathrm{3},\mathrm{1}\right) \\ $$$$ \\ $$$$\mathrm{x}^{\mathrm{3}} +\mathrm{ax}+\mathrm{2}=\mathrm{x}^{\mathrm{3}} +\left(\mathrm{b}+\mathrm{1}\right)\mathrm{x}^{\mathrm{2}} +\left(\mathrm{b}+\mathrm{c}\right)\mathrm{x}+\mathrm{c} \\ $$$$\Rightarrow\mathrm{b}+\mathrm{1}=\mathrm{0}\Rightarrow\mathrm{b}=−\mathrm{1};\:\mathrm{c}=\mathrm{2};\:\mathrm{b}+\mathrm{c}=\mathrm{a}=\mathrm{2}−\mathrm{1}=\mathrm{1} \\ $$$$\Rightarrow\left(\mathrm{a},\mathrm{b},\mathrm{c}\right)=\left(\mathrm{1},−\mathrm{1},\mathrm{2}\right) \\ $$
