Question and Answers Forum

All Questions      Topic List

Differentiation Questions

Previous in All Question      Next in All Question      

Previous in Differentiation      Next in Differentiation      

Question Number 84065 by niroj last updated on 09/Mar/20

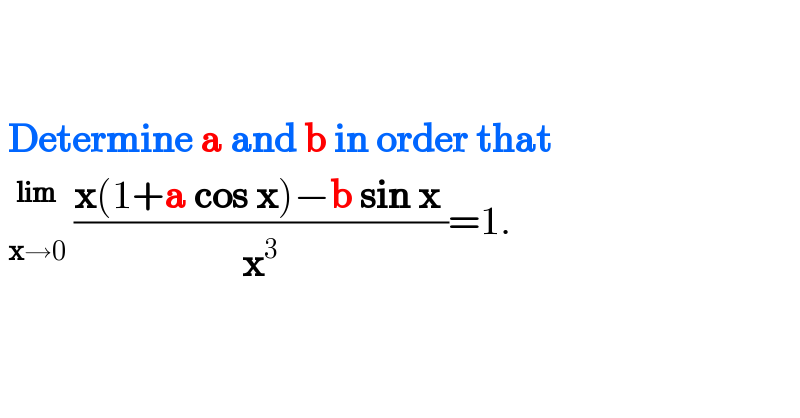
Determine a and b in order that _(x→0) ^(lim) ((x(1+a cos x)−b sin x )/x^3 )=1.

$$ \\ $$$$\: \\ $$$$\:\boldsymbol{\mathrm{Determine}}\:\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{and}}\:\boldsymbol{\mathrm{b}}\:\boldsymbol{\mathrm{in}}\:\boldsymbol{\mathrm{order}}\:\boldsymbol{\mathrm{that}} \\ $$$$\:\underset{\boldsymbol{\mathrm{x}}\rightarrow\mathrm{0}} {\overset{\boldsymbol{\mathrm{lim}}} {\:}}\:\frac{\boldsymbol{\mathrm{x}}\left(\mathrm{1}+\boldsymbol{\mathrm{a}}\:\boldsymbol{\mathrm{cos}}\:\boldsymbol{\mathrm{x}}\right)−\boldsymbol{\mathrm{b}}\:\boldsymbol{\mathrm{sin}}\:\boldsymbol{\mathrm{x}}\:}{\boldsymbol{\mathrm{x}}^{\mathrm{3}} }=\mathrm{1}. \\ $$

Commented by mathmax by abdo last updated on 09/Mar/20

⇒lim_(x→0) ((x(1+acosx)−bsinx)/x^3 )−1 =0 ⇒ lim_(x→0) ((x(1+acosx)−bsinx−x^3 )/x^3 ) =0 ⇒ u(o)=u^′ (0) =u^((2)) (0)=u^((3)) (0)=0 and v(0)=v^′ (0)=v^((2)) (0)=v^((3)) (0)=0 with u(x)=x(1+acosx)−bsinx −x^3 u(0)=0 ⇒0=0 (v) u^′ (x)=1+acosx +x(−asinx)−bcosx−3x^2 u^′ (0)=0 ⇒1+a−b =0 ⇒b=1+a u^((2)) (x) =−asinx −asinx +x(−acosx)+bsinx −6x u^((2)) (0)=0 ⇒0=0 (v) u^((3)) (x)=−2acosx −acosx +axsinx +bcosx −6 u^((3)) (0)=0 ⇒−3a +b −6 =0 ⇒b=3a+6 ⇒1+a=3a+6 ⇒2a+6=1 ⇒ a=−(5/2) and b=−(3/2) (for v the conditions is verified..)

$$\Rightarrow{lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\frac{{x}\left(\mathrm{1}+{acosx}\right)−{bsinx}}{{x}^{\mathrm{3}} }−\mathrm{1}\:=\mathrm{0}\:\Rightarrow \\ $$$${lim}_{{x}\rightarrow\mathrm{0}} \:\:\:\:\:\frac{{x}\left(\mathrm{1}+{acosx}\right)−{bsinx}−{x}^{\mathrm{3}} }{{x}^{\mathrm{3}} }\:=\mathrm{0}\:\Rightarrow \\ $$$${u}\left({o}\right)={u}^{'} \left(\mathrm{0}\right)\:={u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)={u}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\mathrm{0}\:\:{and}\:{v}\left(\mathrm{0}\right)={v}^{'} \left(\mathrm{0}\right)={v}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)={v}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\mathrm{0}\:{with} \\ $$$${u}\left({x}\right)={x}\left(\mathrm{1}+{acosx}\right)−{bsinx}\:−{x}^{\mathrm{3}} \\ $$$${u}\left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\mathrm{0}=\mathrm{0}\:\left({v}\right) \\ $$$${u}^{'} \left({x}\right)=\mathrm{1}+{acosx}\:+{x}\left(−{asinx}\right)−{bcosx}−\mathrm{3}{x}^{\mathrm{2}} \\ $$$${u}^{'} \left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\mathrm{1}+{a}−{b}\:=\mathrm{0}\:\Rightarrow{b}=\mathrm{1}+{a} \\ $$$${u}^{\left(\mathrm{2}\right)} \left({x}\right)\:=−{asinx}\:−{asinx}\:+{x}\left(−{acosx}\right)+{bsinx}\:−\mathrm{6}{x}\: \\ $$$${u}^{\left(\mathrm{2}\right)} \left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow\mathrm{0}=\mathrm{0}\:\left({v}\right) \\ $$$${u}^{\left(\mathrm{3}\right)} \left({x}\right)=−\mathrm{2}{acosx}\:−{acosx}\:+{axsinx}\:+{bcosx}\:−\mathrm{6}\: \\ $$$${u}^{\left(\mathrm{3}\right)} \left(\mathrm{0}\right)=\mathrm{0}\:\Rightarrow−\mathrm{3}{a}\:+{b}\:−\mathrm{6}\:=\mathrm{0}\:\Rightarrow{b}=\mathrm{3}{a}+\mathrm{6}\:\Rightarrow\mathrm{1}+{a}=\mathrm{3}{a}+\mathrm{6}\:\Rightarrow\mathrm{2}{a}+\mathrm{6}=\mathrm{1}\:\Rightarrow \\ $$$${a}=−\frac{\mathrm{5}}{\mathrm{2}}\:\:{and}\:{b}=−\frac{\mathrm{3}}{\mathrm{2}}\:\:\:\left({for}\:{v}\:{the}\:{conditions}\:{is}\:{verified}..\right) \\ $$$$ \\ $$

Commented by mathmax by abdo last updated on 09/Mar/20

v(x)=x^3

$${v}\left({x}\right)={x}^{\mathrm{3}} \\ $$

Answered by TANMAY PANACEA last updated on 09/Mar/20

lim_(x→0) ((x{1+a(1−(x^2 /(2!))+(x^4 /(4!))+..)}−b(x−(x^3 /(3!))+(x^5 /(5!))+..))/x^3 ) lim_(x→0) ((x+ax−((ax^3 )/(2!))+((ax^5 )/(4!))−bx+((bx^3 )/(3!))−((bx^5 )/(5!)))/x^3 ) lim_(x→0) ((x(1+a−b)+x^3 ((b/6)−(a/2))+others terms)/x^3 ) 1+a−b=0 (b/6)−(a/2)=1 b−3a=6 1+a−3a=6 −2a=5→a=((−5)/2) b=1+a b=1−(5/2)=((−3)/2)

$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left\{\mathrm{1}+{a}\left(\mathrm{1}−\frac{{x}^{\mathrm{2}} }{\mathrm{2}!}+\frac{{x}^{\mathrm{4}} }{\mathrm{4}!}+..\right)\right\}−{b}\left({x}−\frac{{x}^{\mathrm{3}} }{\mathrm{3}!}+\frac{{x}^{\mathrm{5}} }{\mathrm{5}!}+..\right)}{{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}+{ax}−\frac{{ax}^{\mathrm{3}} }{\mathrm{2}!}+\frac{{ax}^{\mathrm{5}} }{\mathrm{4}!}−{bx}+\frac{{bx}^{\mathrm{3}} }{\mathrm{3}!}−\frac{{bx}^{\mathrm{5}} }{\mathrm{5}!}}{{x}^{\mathrm{3}} } \\ $$$$\underset{{x}\rightarrow\mathrm{0}} {\mathrm{lim}}\:\frac{{x}\left(\mathrm{1}+{a}−{b}\right)+{x}^{\mathrm{3}} \left(\frac{{b}}{\mathrm{6}}−\frac{{a}}{\mathrm{2}}\right)+{others}\:{terms}}{{x}^{\mathrm{3}} } \\ $$$$\mathrm{1}+{a}−{b}=\mathrm{0} \\ $$$$\frac{{b}}{\mathrm{6}}−\frac{{a}}{\mathrm{2}}=\mathrm{1} \\ $$$${b}−\mathrm{3}{a}=\mathrm{6} \\ $$$$\mathrm{1}+{a}−\mathrm{3}{a}=\mathrm{6} \\ $$$$−\mathrm{2}{a}=\mathrm{5}\rightarrow{a}=\frac{−\mathrm{5}}{\mathrm{2}} \\ $$$${b}=\mathrm{1}+{a} \\ $$$${b}=\mathrm{1}−\frac{\mathrm{5}}{\mathrm{2}}=\frac{−\mathrm{3}}{\mathrm{2}} \\ $$

Commented by niroj last updated on 09/Mar/20

exellent dear .thank you so much.

$${exellent}\:{dear}\:.{thank}\:{you}\:{so}\:{much}. \\ $$

Commented by TANMAY PANACEA last updated on 09/Mar/20

most welcome sir

$${most}\:{welcome}\:{sir} \\ $$

Terms of Service

Privacy Policy

Contact: info@tinkutara.com